BUSINESS BOOKS

13.5　極值理論

在第10.4節中，我們介紹了冪律，並且解釋了由冪律出發如何對不同分佈的尾部進行估計。在此我們將討論冪律的理論基礎，並且給出比第10.4節更為複雜的估計過程。描述尾部分佈這一學科的理論被稱為極值理論（extreme value theory，EVT）。在這一節中，我們將討論如何應用極值理論來改善我們對於VaR或ES的估計，以及如何將極值理論應用於高置信水平的VaR的估計，極值理論可以使得對實證分佈（empirical distribution）的尾部的外推變得更加光滑。

13.5.1　主要結果

Gnedenko在1943年證明了極值理論的一個主要結論，^[1]這一結論可以描述多種概率分佈的尾部的狀態。

假定F（v）為變量v的累積分佈函數（例如，在一段時間內組合的損失），u為v的右端尾部的一個數值，v介於u與u+y（y>0）之間的概率為F（u+y）-F（u），v大於u的概率為1-F（u），定義F_u（y）為在v>u條件下，v介於u與u+y之間的條件概率，即

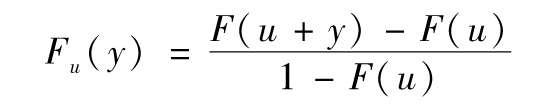
變量F_u（y）定義了右端尾部的概率分佈，即在v>u條件之下，變量v超出u的累積概率分佈。

Gendenko的結果闡明，對於多種概率分佈F（v），分佈F_u（y）（隨著u的增加）趨向於廣義帕累託分佈，廣義帕累託分佈的累積分佈函數為

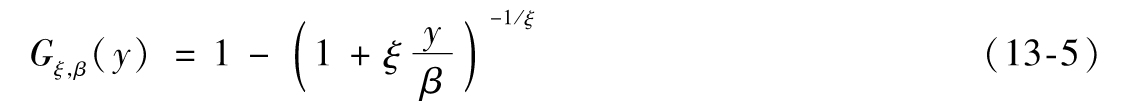
這一分佈中的兩個參數ξ、β必須通過數據來進行估計，參數ξ是有關分佈的形狀，這一參數決定了尾部分佈的肥瘦（heaviness），參數β是分佈的比例因子。

當變量v服從正態分佈時，ξ=0。^[2]當尾部分佈變得越來越肥（重）時，對應的ξ值也越來越大。對於大多數金融數據而言，ξ為正並且介於0.1和0.4之間。^[3]

13.5.2　參數ξ及β的估計

我們可以採用最大似然法來估計參數ξ及β（見第10.9節），將式（13-5）對y求導，我們可以得出概率分佈的密度函數g_ξ,β（y），即

首先我們選定數值u（這一數值可與實證分佈中的95%的分位數較為接近），然後將v的觀察值從大到小進行排序，我們要關注的是那些滿足v>u的觀察值。假定在所有觀察值中有n_u個抽樣大於u，我們將這些觀察值命名為v_i（1≤i≤n_u）。根據式（13-6），假定ξ≠0，這裡的似然函數為

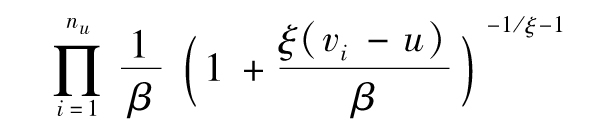
對以上函數求極大值與對其對數求極大值等價，以上函數的對數為

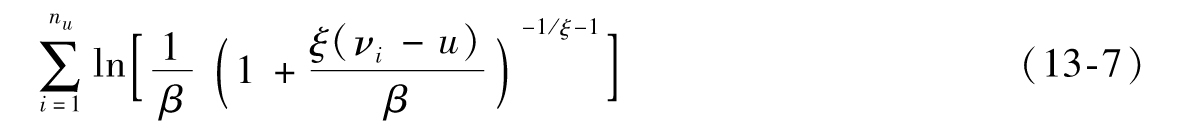
我們可以採用標準的數值程序來求取ξ及β，以使得以上表達式達到極大。Excel提供的Solver程序能給出很好的結果。

13.5.3　對尾部分佈估計

在v>u條件下，v>u+y的概率分佈為1-G_ξ,β（y）；v>u的概率分佈為1-F（u），因此v>x（x>u）的無條件概率分佈為

［1-F（u）］［1-G_ξ,β（x-u）］

如果n為觀察值的總數量，由實證數據所得出的對於1-F（u）的估計值為n_u/n，因此v>x的無條件概率為

13.5.4　與冪律的等價性

令u=β/ξ，式（13-8）可以簡化為

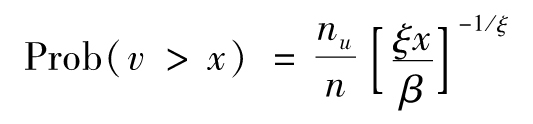
即

Kx^-α

其中

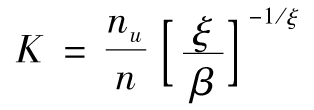
及α=1/ξ，以上過程證明了式（13-8）與第10.4節中的冪律等價。

13.5.5　左端尾部

截至目前，我們只討論了v的概率分佈的右端。如果我們對分佈的左端感興趣，則可以採用-v而不是v來計算。例如，假定一家石油公司已經採集了每天石油價格百分比變化的數據，並想求得1天內、99.9%概率下，石油價格的下跌不會被超出的數量。該數量可以從石油價格增長的左端概率分佈中得出。在分析中，石油公司可以改變每個數據的符號（描述價格增長的數據會變為下跌數據），並採用以上的辦法來進行分析。

13.5.6　計算VaR和ES

為了計算對應於置信水平為q的VaR，我們需要對以下方程求解

F（VaR）=q

因為F（x）=1-Prob（v>x），由式（13-8）得出

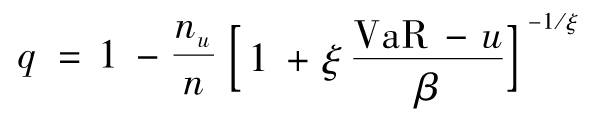
因此

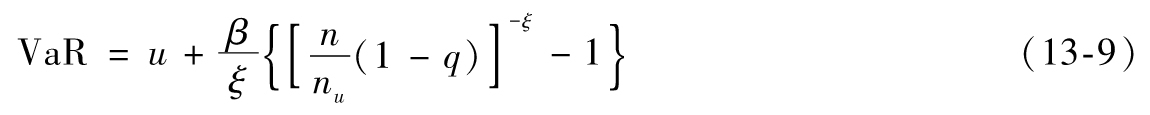
預期虧空如下

[1] See D. V. Gnedenko, “Sur la distribution limité du terme d’une série aléatoire,” Annals of Mathematics 44(1943):423-453.

[2] 當ξ=0時，廣義帕累託分佈形式為G_ξ,β(y)=1-exp(-y/β)。

[3] 由式（13-5）所定義的分佈在k≥1/ξ時，v的分佈的k階矩E（v^k）為無窮大；正態分佈的所有階矩均為有限；當ξ=0.25時，分佈的矩只有前三階為有限；當ξ=0.5時，分佈的矩只有第一階為有限，等等。