e1 John Hull 風險管理與金融機構 v5
13.2 VaR的精確度
在歷史模擬法中,對於交易組合價值變化分佈的估計是基於過去發生的有限的觀察值,正因為如此,歷史模擬法對分佈的分位數的估計並不是絕對精確的。
Kendall和Stuart(1972)的研究結果給出了由抽樣數據所計算出的概率分佈的分位數的置信區間。[1]假定概率分佈的第q個分位數的估計值為x,這一估計的標準誤差為
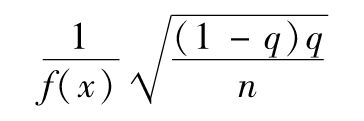
其中n為觀察值的個數,f(x)為對應於損失量為x的損失分佈的密度函數值,這一函數值可以通過將經驗數據與已知分佈進行匹配來估計。
【例13-1】 假如我們採用500個觀察數據來估計損失分佈的99%分位數(第99個分位數),這時n=500,q=0.99。我們可以通過採用某性質已知的標準分佈來對實證數據進行擬合,並由此來求得f(x)的近似值。假定我們選擇正態分佈作為該標準分佈,最佳擬合參數分別為期望值為0,標準差為1 000萬美元。在Excel中,99%分位數所對應數值為NORMINV(0.99,0,1 000)=2 326萬美元,f(x)的取值為
NORMDIST(2 326,0,1 000,FALSE)=2.7
分位數估計值的標準誤差為
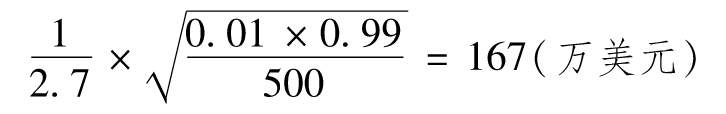
假如採用歷史模擬法所求取的0.99分位數的估計值為2 500萬美元,在95%置信程度下VaR的置信區間為2 500-1.98×167~2 500+1.96×167,即2 170萬~2 830萬美元。
例13-1說明,歷史模擬法所求得VaR的估計的標準誤差較大,隨著置信度的下降,標準誤差也會降低。例如,假定例13-1中VaR所對應的置信程度為95%而不是99%,標準誤差會由167萬美元降至95萬美元。標準誤差隨著抽樣數據數量的增加會有所降低,但標準誤差的大小僅僅與數據量的平方根成反比。如果將例13-1所對應的抽樣數據增加3倍,即由500個增至2 000個,標準誤差僅減小一半,即由167萬美元降至83萬美元。
另外,我們應該認識到歷史模擬法假設市場變量每天變化的聯合分佈是不隨時間的推移而變化的。這一條件在計算VaR過程中往往不完全成立,因此,這對VaR的估計增加了一定的不確定性。
對於表13-1~表13-4的數據,損失的均值(以千美元計)為0.870,標準差為93.698。假定損失服從正態分佈,採用與例13-1類似的計算得出,f(x)為0.000 284,估計的標準誤差(以千美元計)等於

VaR等於253 385美元,相應的95%的置信區間為[220 000美元,280 000美元]。
對於損失估計,採用正態分佈的假設並不一定很好,這是因為損失分佈比正態分佈有更肥大的尾部(表13-1和表13-2中數據的損失分佈的超額峰度為4.2)。要獲得更好的標準誤差估計,f(x)可被假設為服從帕累託分佈(Pareto distribution),我們在第13.5節中將對這一分佈進行討論。
[1] See M. G. Kendall and A. Stuart, The Advanced Theory of Statistics, vol.1, Distribution Theory, 4th ed. (London: Charles Griffin, 1972).