e1 John Hull 風險管理與金融機構 v5
13.1 方法論
歷史模擬法以歷史數據為依據來預測將來。假設,我們採用過去501天的歷史數據來計算1天展望期對應於99%置信水平的VaR(這裡選擇的展望期及置信水平是市場風險管理過程中一種典型的選擇,在實際計算中常常流行採用501天的歷史數據,並由此產生500個情景)。
歷史模擬法的第一步是選定影響交易組合的風險源,這些風險源可能是匯率、股價、利率等,然後我們需要收集這些風險源在過去最近501天的數據,通過這些數據我們可以得出從今天到明天市場變量的500種不同變化情景。我們將數據開始的第1天記為D0(day 0),數據開始的第2天記為D1(day 1),依此類推。情景1(scenario 1)是指由D0到D1所對應數據的變化比率;情景2是指由D1到D2所對應數據的變化比率,依此類推。對於每一個情景,我們可以計算從今天到明天的交易組合的價值變化,由此我們可以得出交易組合日損失(即收益為負)的概率分佈圖,分佈中所對應的99%的分位數是500個計算數值中第5個最壞的損失,VaR的估計值是第99個百分比分位數所對應的損失。[1]假如市場變量的變化是從過去500天提取出來的,這些變量的變化代表從今天到明天變化的不同可能,那麼我們可以有99%的把握肯定,交易組合所對應的損失會小於VaR的估計值。ES是損失分佈中1%的尾部分佈的平均損失。VaR是第5個最大損失值,因此,ES的估計值是比VaR更大的損失的平均值(即第4個最大損失值)。[2]
採用代數符號描述這一過程,我們將某市場變量在第i天所對應的數值記為vi,假定今天為第n天,歷史模擬法產生的市場變量在明天所對應的第i個情景為

對於某些變量,如利率、信用價差和波動率,考慮市場變量的實際變化而不是百分比變化,那麼式(13-1)變為
vn+vi-vi-1
為了簡化討論,在本章的其餘部分中,我們將假設歷史模擬基於潛在市場變量的百分比變化。
13.1.1 過程說明
為了說明計算過程,假定一個投資者在2008年9月25日持有一個價值為1000萬美元的投資組合,組合中有4個股票指數:美國道瓊斯工業指數(DJIA)、英國富時100指數(FTSE 100)、法國巴黎40指數(CAC 40)以及日本日經225指數(Nikkei 225)。每個指數在2008年9月25日的取值如表13-1所示,讀者可以在作者網站上下載含有這4個指數過去501天收盤價格的歷史數據及計算VaR的Excel表單,見www-2.rotman.utoronto.ca/~hull/RMFI/VaRExample,[3]本節中用的計算可以在工作表1~3中找到。
表13-1 用於演示VaR計算過程的投資組合

因為我們考慮的是一個美國的投資者,所以FTSE 100、CAC 40和Nikkei 225這些指數都應該以美元計價。例如2008年8月10日,FTSE 100為5 823.40點,而匯率為1英鎊元兌換1.891 8美元。這意味著,以美元計價的指數為5 823.40×1.891 8=11 016.71。表13-2顯示了以美元計價的指數數據的一部分。
表13-2 採用歷史模擬法計算VaR所需要的股票指數數據 (美元)
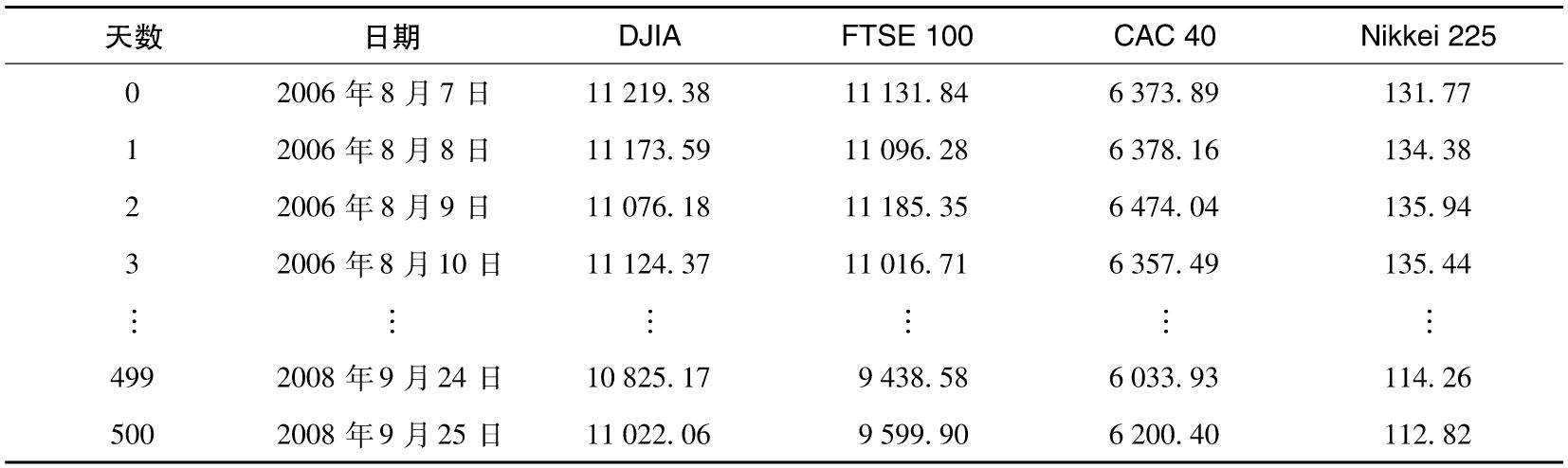
2008年9月25日是檢驗股票投資表現非常有意思的一天。2007年8月開始的信用危機已經持續了1年,股票價格持續下跌了幾個月。在這期間,波動率增大,雷曼兄弟在10天前已經申請破產,美國財政部的7000億美元受困資產救助資金(trouble asset relief program,TARP)還沒有在國會通過。
表13-3顯示了市場變量在2008年9月26日對於選定情景的取值。情景1(表13-3的第1行)是在假定9月25日和26日的市場價格百分比變化等同於2006年8月7日和8日市場價格的百分比變化的情景下,市場變量在2008年9月26日的預測值;情景2(表13-3的第2行)是在假定9月25日和26日的市場價格百分比變化等同於2006年8月8日和9日市場價格的百分比變化的情景下,市場變量在2008年9月26日的另一種預測;依此類推。一般來講,情景i(表13-3的第i行)假定9月25日和26日的市場價格百分比變化等同於歷史數據中第i-1天與第i天的百分比變化(1≤i≤500),情景i定義了市場變量在2008年9月26日的第i種預測。表13-3中的500行就是我們考慮的500個情景。
表13-3 由表13-2的數據所產生的對於2008年9月26日市場變量的不同情景 (所有指數以美元計)
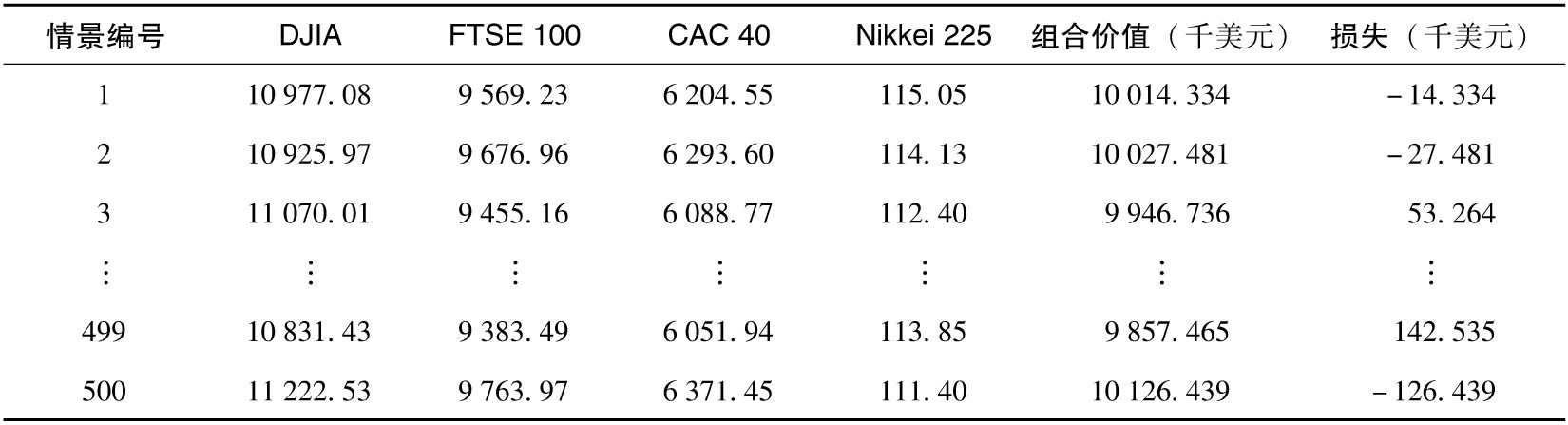
2008年9月25日,DJIA的值為11 022.06,2006年8月7日為11 219.38,2006年8月8日下跌為11 173.59,因此,DJIA在情景1下的預測值為
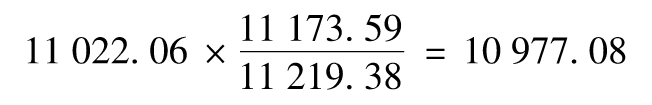
與此類似,在情景1下,FTSE 100、CAC 40、Nikkie 225的預測值分別為9 569.23、6 204.55和115.05。因此在情景1下,組合資產價值為(以千美元計)
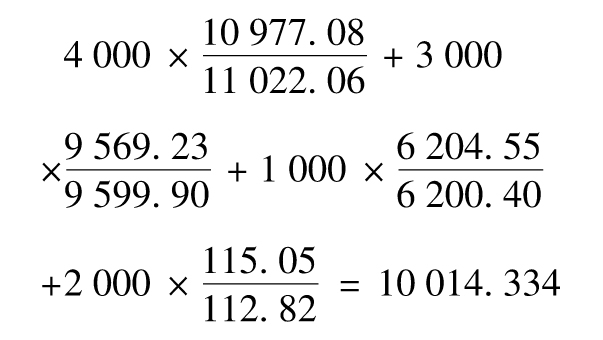
在情景1下,組合收益為14334美元,對於其他情景,我們可以進行類似的運算。在圖13-1中,我們展示了損失分佈的直方圖(柱條代表損失(以千美元為計)出現在450~550、350~450、250~350的次數)。
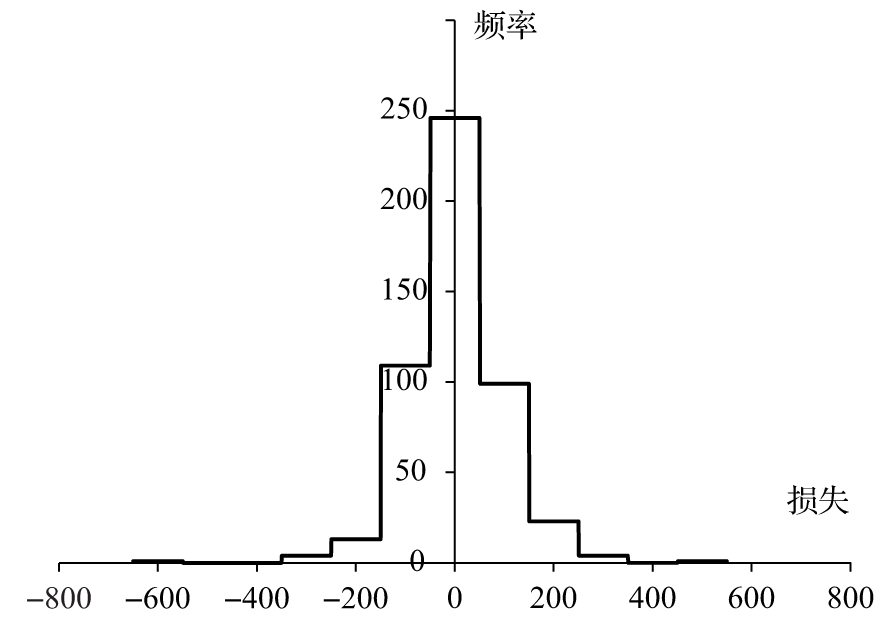
圖13-1 2008年9月25日和26日損失分佈的直方圖(頻率圖)
然後我們將500個不同的損失進行排序,最終結果的一部分被展示在表13-4中,損失最糟糕的情景對應於情景494(其股指變化對應於雷曼兄弟破產那一天的股指變化)。在1天展望期及99%置信區間下,VaR對應於損失中第5個最糟的情景,為253 385美元。
表13-4 對應500個情景損失的排序

如第12.6節所示,10天展望期及99%置信區間的VaR等於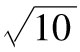 乘以1天展望期及99%置信區間的VaR,10天的VaR等於
乘以1天展望期及99%置信區間的VaR,10天的VaR等於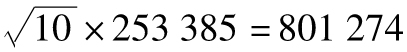 美元。
美元。
在我們的例子中,每天計算VaR時,都應採用最近501天的數據。例如,考慮2008年9月26日(第501天)的情景,我們可以確定所有市場變量所對應的新值,並計算出相應的交易組合的價值。我們可以根據前面描述的過程來求得一個新的VaR。在計算中將採用2006年8月8日~2008年9月26日(第1天到第501天)的數據(我們可以由市場變量的百分比變化來確定500個觀察值,2006年8月7日,即第0天的數據將不再會被使用)。類似地,在下一個交易日,即2008年9月29日(第502天),在計算VaR時,我們將採用2006年8月9日~2008年9月29日的數據;依此類推。
在實際中,一個銀行的交易組合遠比我們在這裡考慮的情形要複雜,銀行的交易組合可能會包括成千上萬的頭寸,銀行的某些頭寸常常是遠期合約、期權和其他衍生產品,而且交易組合本身也在不斷變化。如果一家銀行的交易使得組合變得風險更大,10天展望期的99%VaR一般會增大;如果交易使得組合變得風險更小,10天展望期的99%VaR一般會減小。對於任意一天VaR的計算,我們須假定組合頭寸在兩個交易日之間保持不變。
在計算VaR時,我們考慮的市場變量包括匯率、商品價格和利率等。對於利率,為了能夠對相應的交易組合定價,銀行常常需要不同貨幣的由短期國債、LIBOR和OIS所生成的零息利率期限結構的信息。生成這些期限結構的互換利率和債券收益率就是VaR計算所考慮的市場變量(見附錄B)。任意貨幣的零息曲線都可能會涉及十幾個市場變量。
13.1.2 ES
使用歷史模擬來計算ES時,我們可將觀察到的損失分佈的尾部值取平均。在上面的例子中,最壞的4個情景(以千美元計)是494、339、349和329(見表13-4)。這些情景的平均損失為345630美元,這就是我們對ES的估計。
13.1.3 壓力VaR和壓力ES
前面給出例子中,計算某日的VaR或ES時,我們總是用最近的數據來進行歷史模擬。例如,在第4個例子中,計算VaR或者ES時,我們用到的是最近501天的歷史數據。我們將以此方式計算的VaR和ES稱為當前VaR和當前ES,但實際上,歷史模擬法可採用過去任意時間段的數據。使用波動率較高的時段的數據,預測出的VaR和ES就會較高;使用波動率較低的時段,預測的VaR和ES就會較低。
監管機構已經引入了被稱作壓力VaR和壓力ES的風險測度。要計算這些測度,金融機構首先要尋找一個251天的時間段。在這251天的時間段中,其現有投資組合的VaR或者ES會最大。然後,這251天的歷史數據會扮演前面例子中501天時間段中數據的角色。251天中第0天和第1天之間的市場變化被用來產生情景1,第1天和第2天之間的變化被用來產生情景2,依此類推,這樣總共會生成250個情景。展望期為1天、置信度為99%的壓力VaR是第二大損失和第三大損失之間的中間值。展望期為1天、置信度為99%的ES的估計量是兩個最大損失的平均值。[4]
[1] 在這裡我們有不同的選擇,在這時我們既可以選取第5個最壞或第6個最壞所對應的數值,或者第5個最壞及第6個最壞的平均值,來作為500個抽樣數據中的1%的分位數。在採用Excel計算表的PERCENTILE函數時,假定有n個觀察值,k為某個整數,k/(n-1)分位數是對應於觀察值名列第k+1的數據值,而其他的分位數由線性插值計算求得。
[2] 第1個頁下注指出,可以根據離散數據估算出其他的VaR值。ES也是如此。例如,我們可以對5個最壞的觀察結果取平均值(包括VaR估計值)。另外,我們也可以將第5個最大損失值的權重設為其他4個值權重的一半。這裡提出的建議似乎符合市場慣例。
[3] 為了簡化例子的計算,我們只包括了所有4個股指都開放交易的日期。這解釋了我們為什麼需要2006年8月7日~2008年9月25日這麼長的時間段來提取501個數據。在實際中,在對美國的金融機構進行分析時,我們要對非美國假日的數據進行補充。
[4] 這些不是唯一的方法。VaR可以估計為第三大損失值或第二大損失值(美國聯邦儲備委員會等一些監管機構更喜歡後者)。ES的算法是0.4c1+0.4c2+0.2c3,其中c1、c2、c3是三個最大的損失值,並且c1>c2>c3。