e1 John Hull 風險管理與金融機構 v5
12.10 回溯測試
回溯測試是一種重要的衡量風險測度在現實中的表現的手段。在回溯測試中,我們會驗證當前採用的風險測度計算過程如果被用於過去,其表現會如何。對VaR的回溯測試會比ES更簡單,這也解釋了為什麼過去監管機構並不情願把用於市場風險的VaR模型轉換為ES模型。在第18章中我們會解釋,監管部門的計劃是在將來,ES模型會被用來計算監管資本金,而回溯測試還是會依賴VaR的測算。
假設我們開發出一個計算1天的99%VaR的模型。在回溯測試中,我們要找出來交易組合在1天內的損失有多少次超出了1天的99%VaR,實際損失超出VaR情形被稱為例外(exception)。如果例外的天數大約佔整體天數的1%,則我們應該對我們的VaR模型表現感到欣慰。但是,如果例外的天數佔整體天數的比例遠大於1%(例如7%),則我們有理由認為VaR的估計偏低。從監管部門的角度來看,由這樣的VaR而得出的資本金數量會太低。此外,如果例外情形發生的頻率遠低於1%(例如0.3%),則我們有理由認為這裡的VaR估計偏高,由此而得出的資本金數量偏高。
在對1天的VaR進行回溯測試時,我們要考慮在日內交易組合本身的變化。對這一問題有兩種處理方式:第一種方式是假定交易組合的構成沒有任何變化,在這一假設之下,我們可以計算交易組合的價值變化,完成計算之後,將VaR與這一理論價格變化(hypothetical changes)進行比較;第二種方式是將VaR同交易組合價值的真實變化進行比較。在VaR的計算過程中,我們必然要假設在展望期內沒有任何新的交易,正因為如此,將VaR同第一種方式中計算所得的理論價格變化進行比較看起來更為合理。但是,在我們的分析過程中,交易組合的實際價格變化才是我們管理的重心。在實踐中,風險管理人員常常將VaR既同理論價值變化進行比較,也同實際價值變化進行比較(事實上,監管機構堅持在回溯測試中,VaR要與交易組合的真實及理論價值變化同時進行比較)。在計算真實價格變化時,一些與市場風險無關的項目必須被剔除出來,這些項目包括手續費收入及一些非市場中間價格的交易(買入與賣出價格的平均)帶來的損益等。
假定VaR的展望期為1天,置信度為X%。如果VaR模型準確無誤,那麼每天的損失超出VaR的概率p=1-X/100。假定我們總共有n個觀察日,在所有的觀察日中有m天損失超出了VaR。假定m/n>p,因為VaR的估計太低,我們在這裡應該拒絕這個模型嗎?將我們的問題表達得更正式一些,我們考慮以下兩種對立假設:
(1)對應任意一天,例外發生的概率為p;
(2)對應任意一天,例外發生的概率大於p。
這裡的例外是指實際損失超出了VaR的估計。從二項式分佈的性質得出,有m或更多天的天數損失超出VaR的概率為
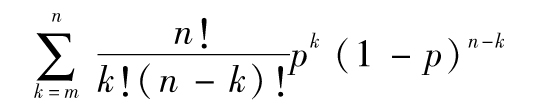
以上計算可通過Excel中的函數BINOMDIST來實現,在統計假設檢驗中,一個經常被選定的置信度為5%,如果在所有觀察日中,有m或更多天實際損失超出VaR的概率小於5%,那麼我們可以拒絕第一種假設,即例外發生的概率為p;當m或更多天實際損失超出VaR的概率大於5%時,我們不能拒絕第一種假設。
【例12-14】 假定我們採用600天的數據來檢測VaR模型,在計算VaR時我們選取了99%的置信區間,在600天觀察數據中我們發現了9個例外,而在這裡我們對例外所發生的個數的期望值為6,這時我們應該拒絕這一VaR模型嗎?通過Excel計算,對應於9個或更多的例外發生的概率為1-BINOMDIST(8,600,0.01,TRUE),以上的計算數值為0.152,因此如果採用5%置信區間,我們不應該拒絕模型。但是假如我們發現例外的個數為12,我們計算出的例外個數為12或更多的概率為0.019,這時我們應該拒絕模型。事實上,當例外個數超出11時我們就應該拒絕模型(例外個數為10或更多的概率大於5%,但例外個數為11或更多的概率小於5%)。
當例外個數m小於例外的期望值時,我們可以採取一個類似的方法來檢驗例外發生的真正概率是否為1%(在這時,我們的對立假設為例外發生的概率小於1%)。此時有m個或更少例外發生的概率為
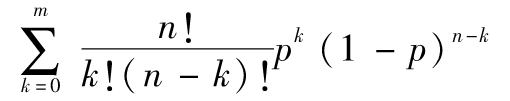
這一數值要與5%閾值來進行比較。
【例12-15】 假定我們採用600天的數據來檢測VaR模型,在計算中我們選用99%的置信程度,在600天觀察數據中我們只發現了1個例外,這一數值遠低於例外的期望值6,這時我們應該拒絕VaR模型嗎?用Excel計算有1個或沒有例外發生的概率為BINOMDIST(1,600,0.01,TRUE)。
以上的計算數值為0.017,因此如果採用5%的置信區間,我們應該拒絕模型,但是,如果例外發生的次數大於或等於2個,那麼我們就不應該拒絕模型。
在這裡我們所考慮的檢驗均為單向檢驗。在例12-14中,我們假定例外發生的概率是1%或者大於1%,在例12-15中我們假定例外發生的概率是1%或者小於1%。Kupiec(1995)開發出一個很有效的雙向檢驗[1](two-tailed test)方法。假定在VaR中例外發生的概率為p,而在n個觀察日中例外發生了m次,變量
-2ln[(1-p)n-mpm]+2ln[(1-m/n)n-m(m/n)m]
(12-11)
應該服從具有一個自由度的chi-平方分佈(chi-square distribution)。當例外發生的次數很高或者很低時,由式(12-11)所計算的統計量會較大。在一個自由度的chi-平方分佈中,統計量大於3.84的概率為5%,因此,當式(12-11)所計算出的值大於3.84時,我們就可以拒絕模型。
【例12-16】 假設在以上兩個例子,我們採用600天的數據來檢驗VaR模型,VaR的置信度仍為99%,當例外出現的次數小於等於1或者大於等於12時,由式(12-11)計算出的統計量大於3.84,因此當2≤m≤11時,我們接受VaR模型,否則,我們拒絕模型。
一般來講,當VaR置信度增大時,回溯測試的難度也會提高。因此,有觀點認為,應使用相對較低的置信區間來計算VaR,以方便進行回溯測試,然後再使用極值理論(見第13章)來得到足夠高的置信度。
聚束狀態
除了例外發生的頻率這個問題外,我們還要討論聚束狀態(bunching)。如果交易組合的每天價值變化是獨立的,那麼例外的發生應該比較均勻地分佈在回溯測試的區間之內。在實踐中,我們發現例外的發生往往聚束在一起,這說明了連續交易日之間的損失分佈並非獨立。一種檢測聚束狀態的方法是採用由Christofferson(1998)提出的統計量[2]
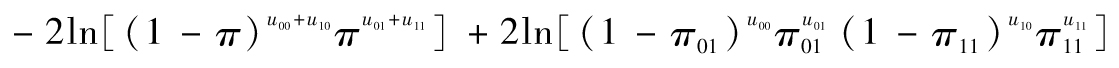
其中uij為在某天我們處在i狀態而在第二天處在j狀態產生的次數。當聚束狀態不存在時,以上定義的統計量服從有一個自由度的chi-平方分佈,這裡狀態0定義為某一天沒有例外發生,而狀態1定義為在某一天有例外發生,再有
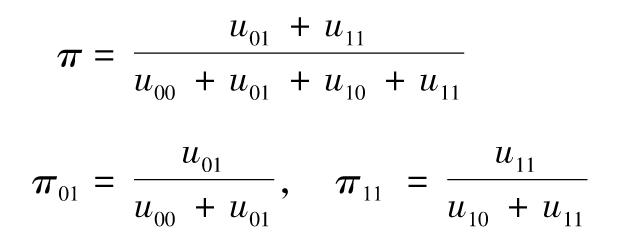
[1] See P. Kupiec, “Techniques for Verifying the Accuracy of Risk Management Models,” Journal of Derivatives 3(1995):73-84.
[2] See P. F. Christoffersen, “Evaluating Interval Forecasts,” International Economic Review 39(1998):841-862.