e1 John Hull 風險管理與金融機構 v5
12.8 歐拉定理
由偉大的數學家萊昂哈德·歐拉(Leonhard Euler)很多年前發現的一個結果被證明在將一個風險測度指標由整個投資組合向子組合分配時有重要的作用。令V是一個交易組合上的風險測度,而xi是第i個子組合的大小(1≤i≤M)。假設所有的xi,當xi變為λxi時(即整個交易組合變為原來的λ倍),V變為λV。這對應於第12.5節所述的第三個條件,即線性同質性,這對大部分風險測度是成立的。[1]
基於上述條件,由歐拉定理,下式是成立的

這一結果提供了將V分配到各個子組合中的方法。
當風險測度為VaR時,根據歐拉定理

這裡,Ci是式(12-8)中給出的第i個子交易組合的成分VaR。這一結果表明,一個交易組合的成分VaR的總和等於交易組合的整體VaR。因此,成分VaR可以方便地將整體VaR分配到子交易組合中。如在前一節中解釋的,成分VaR的另一個吸引人的性質是:一個大交易組合的第i個成分VaR與這一成分的遞增VaR近似。
當以ES為風險測度時,歐拉定理同樣顯示交易組合的整體ES是所有成分ES的和:
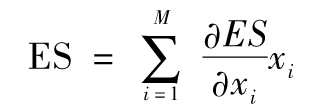
由此,與VaR類似,ES也可以被分配到各個不同的業務部門中。在第26章中,我們會介紹怎樣使用歐拉定理對銀行的經濟資本金在各個業務部門中進行分配。
通過歐拉定理,交易組合的風險可以按組成成分被分解,這對確定所謂的風險預算(risk budgeting)非常有用。風險預算的目的就是在交易組合的不同組成成分之間分配風險。如果通過歐拉分解發現分配給某一成分的風險過高,則交易組合就需要重新調整。
[1] 對一個納入了流動性的風險測度可能不成立。當一個交易組合變得很大時,它的流動性會變差。