e1 John Hull 風險管理與金融機構 v5

12.6　VaR和ES中的參數選擇

用戶在計算VaR或者ES時須設定兩個參數：時間展望期及置信度。一個較為普遍的假設是假定交易組合價值變化在某指定展望期服從正態分佈，但正如我們在第10.3節中討論的，一般來說，這並不是一個好的假設。但是在此，討論一下這個假設下的結果還是有意義的。設交易組合損失的均值為μ，標準差為σ

VaR=μ+σN-1（X）

（12-1）

其中X為置信度，N-1（·）代表累積正態分佈的反函數（在Excel計算表中，這一項的計算可以通過調用函數NORMSINV來實現）。上式顯示出，對於一個相對較短的時間展望期，μ通常被假定為0，且對應於一定的置信度，VaR與σ成正比。

【例12-9】　假定某交易組合在10天展望期上的價值變化服從正態分佈，分佈的期望值為0，標準差為2 000萬美元，10天展望期的99%的VaR為2 000N-1（0.99）=4 650萬美元。

假設損失服從正態分佈，均值為μ，標準差為σ，置信區間為X的ES為

這裡Y是標準正態分佈第X分位數對應的值（即它是均值為0和標準差為1的標準正態分佈上，有1-X概率被超過的點）。從這裡也能看出，如果假設μ的值為0，則ES和VaR類似，也與σ呈正比。

【例12-10】　再次考慮例12-9，10天內組合價值的變化服從一個均值為0、標準差為2 000萬美元的正態分佈。因為標準正態分佈上有1%概率被超過的點為2.326，所以10天展望期、置信度為99%的ES是：（萬美元）。

12.6.1　時間展望期

在計算VaR和ES時，時間展望期的選取要因用途而定。當持倉的流動性很好，交易活躍時，則使用較短的（可能僅有幾天）展望期是合理的。當得出的風險測度不可接受時，管理人員應對交易組合及時進行調整。在這種情況下，一個較長展望期的風險測度意義不大，這是因為在一個較長的展望期內，交易組合的成分往往已經發生較大的變化。

養老基金投資組合的管理人員往往會選擇一個較長的展望期。這是因為此類投資組合的交易行為往往不太活躍，而且組合內的某些資產的流動性也不一定很好。當投資組合的流動性從一種工具變化到另一種工具時，可以更改VaR或ES的定義，以使所考慮的變化從一個市場變量到另一個市場變量都不同。例如，考慮一個由IBM的股票和每年交易少於10次的公司債券組成的投資組合。從IBM的價格變化和債券價格的變化計算出一種風險測度是合理的，其中，我們有99％的把握認為IBM的價格變化將在10天之內不會被超過，有99%的把握認為債券價格的變化不會在60天之內被超過。這是監管機構在《交易賬戶的基本審查》中所採用的方法，將在第18章中進行討論。

無論對應於什麼樣的場合，在考慮市場風險時，風險管理人員往往要首先計算1天展望期的VaR或者ES，對於其他的展望期，一個較為常用的假設為

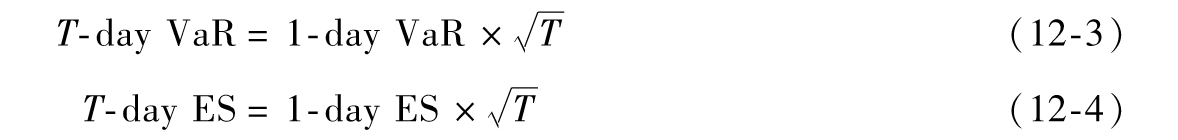
當交易組合價值的日間變化相互獨立，並服從相同的期望值為0的正態分佈時，以上公式完全正確；對於其他情形，這個公式只是一個近似式。以上公式基於式（12-1）和式（12-2）及以下結果事實：

（1）T個相互獨立並具有等同分佈的標準差等於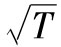乘以任意一個分佈的標準差；

（2）多個相互獨立正態分佈的總和仍服從正態分佈。

12.6.2　自相關性的影響

在實際中，投資組合價值每天的變化並不總是相互獨立的，定義ΔPi為交易組合在第i天的價值變化，一個較為簡單的假設是一階自相關，即對所有的i，假定ΔPi與ΔPi-1的相關係數均為ρ。假定對於任意i，ΔPi的方差為σ2，採用兩個變量之和的方差公式，我們得出ΔPi-1+ΔPi的方差為

σ2+σ2+2ρσ2=2（1+ρ）σ2

令ΔPi-j與ΔPi的相關係數為ρj。因此，我們得出以下計算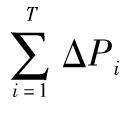的標準差的計算公式（見練習題12.11）

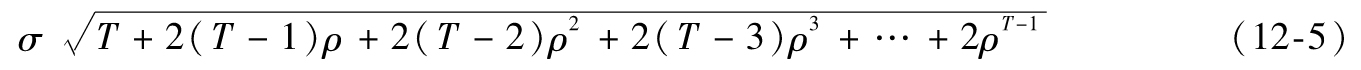
表12-1展示了由1天VaR來計算T天VaR時，自相關性（autocorrelation）的影響。在計算中，我們假設交易組合每天價值變化均服從正態分佈，期望值為0。我們應該注意到T天的VaR（ES）和1天的VaR（ES）的比率與每天波動率σ以及置信度均無關，這一結論是基於式（12-1）、式（12-2）及式（12-5）的性質，即T天標準差與1天標準差成正比。將表12-1中ρ=0情形與其他情形進行比較得出：當自相關存在時，由式（12-3）和式（12-4）所估計的VaR和ES會偏低。

表12-1　當存在一階自相關性時，T天的VaR（ES）同1天的VaR（ES）的比率

注：在計算中，我們假定組合的每天價值變化均服從正態分佈，期望值為0，ρ為自相關參數。

【例12-11】　假定某交易組合的每天價值變化服從正態分佈，均值為0，標準差為300萬美元，每天價值變化的一階自相關係數為0.1，由式（12-5）得出，在今後5天交易組合的價值變化的標準差為

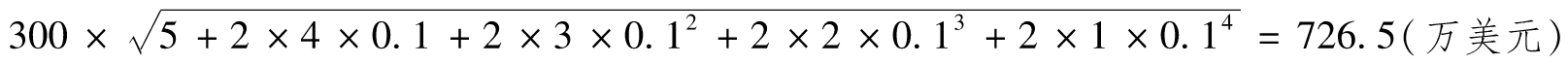
因此5天的95%VaR為：726.5N-1（0.95）=1 195（萬美元）；5天的ES為：726.5×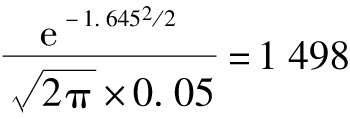（萬美元）。

注意5天價值變化的標準差同1天價值變化的標準差的比率為726.5/300=2.42。在我們的假設之下，VaR及ES均與標準差成正比，這裡的計算正好對應於表12-1中ρ=0.1及T=5的情形。

12.6.3　置信區間

VaR和ES中選用的置信區間與若干因素有關。假定一家銀行想保持自己的AA信用評級，銀行通過計算得出，具有AA信用評級的公司在1年展望期內只有0.03%的破產可能，因此，銀行在內部管理過程中可以採用99.97%置信區間，並且採用1年的展望期來計算資本金。例如，如果對所有敞口，展望期為1年、置信度為99.97%的VaR為50億美元，則意味著如果銀行擁有50億美元資本金，在1年內破產（即將所有股本損失掉）的可能性只有0.03%。銀行也可將這一信息傳達給評級公司，這一信息表明銀行有資格得到AA信用評級。

在實際計算中所採用的置信區間往往比在銀行報告中採用的置信區間要小得多，這是因為對應於高置信區間VaR的估計會非常困難。提高置信區間的一個常用做法是我們將在第13章中介紹的極值理論。如果每天的價值變化服從正態分佈，期望值為0，那麼我們可以採用式（12-1）與式（12-2）來轉換對應於不同置信區間的VaR和ES。例如，假定σ為對應於某展望期交易組合價值變化的標準差，交易組合價值變化的分佈的期望值為0，對應於置信區間為X的VaR估計為VaR（X），預期虧空為ES（X）。由式（12-1）得出

VaR（X）=σN-1（X）

以上公式對不同置信區間X均成立，由此我們可知置信區間為X*的VaR，可以由更低的置信區間X的VaR得出

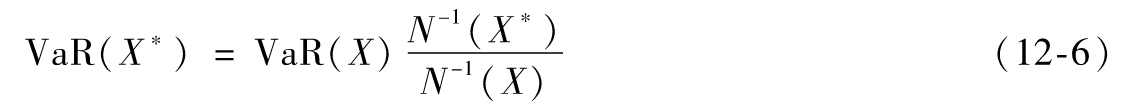
類似地，由式（12-2）

這裡，Y和Y*是標準正態分佈上各有（1-X）和（1-X*）概率被超過的值。

式（12-6）和式（12-7）假定兩個VaR和ES測度具有同樣的展望期，如果我們想同時變換展望期和置信區間，則可以將上述兩式分別與式（12-3）及式（12-4）結合進行計算。

【例12-12】　假定某交易組合1天的95% VaR為150萬美元，1天展望期、95％置信度的ES為200萬美元，同時假定交易組合的價值變化服從正態分佈，均值為0，由式（12-6）得出，1天展望期的99% VaR為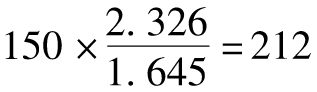：（萬美元）。由式（12-7）可知，1天展望期、99%置信度的ES為：（萬美元）。