e1 John Hull 風險管理與金融機構 v5
12.5 一致性風險測度
假定對應於99.9%置信區間和1年展望期,某交易組合的VaR為5 000萬美元,這意味著在極端條件下(理論上講,每1 000年出現一次),金融機構在1年時損失會超出5 000萬美元,這同時也說明,如果金融機構持有5 000萬美元的資本金,我們會有99.9%的把握,金融機構不會在1年內完全損失自身持有的資本金。
假定我們想設計某種風險測度來確定金融機構應持有的資本金數量,VaR是最好的選擇嗎(在合適的展望期和置信水平下)?Artzner等研究人員對這一問題進行了研究,他們指出理想的測度應滿足以下性質[1]:
(1)單調性(monotonicity):如果在任何情形下,第一個交易組合的回報均低於另一個交易組合的回報,那麼第一個交易組合的風險測度一定要比另一個更大。
(2)平行移動不變性(translation invariance):如果我們在交易組合中加入K數量的現金,那麼交易組合所對應的風險測度要減少K數量。
(3)同質性(homogeneity):假定一個交易組合的內含資產品種和相對比例不變,但內含資產的數量增至原數量的λ倍,此時新的交易組合的風險測度應是原風險的λ倍。
(4)次可加性(subadditivity):兩個交易組合相加所組成的一個新交易組合的風險測度小於或等於最初兩個交易組合的風險測度之和。
以上風險測度的第一個性質顯而易見,如果一個交易組合的回報總是比另一個交易組合要差,那麼第一個交易組合的風險一定會更高;第二個條件也非常合理,如果我們在某個交易組合中加入K數量的現金,那麼該現金可以為損失提供緩衝,相應的額外資本金要求也應該可以減少K數量;第三個條件也很合理,如果我們將某交易組合放大兩倍,那麼相應的資本金要求也應該增大兩倍;[2]第四個條件是在說明風險分散可以降低風險,即我們將兩個交易組合疊加在一起,新的交易組合的風險應該減少,或至少保持不變。
VaR滿足以上討論中的前3個條件,但VaR並不一定永遠滿足第四個條件,這一點將在以下例子中闡明。
【例12-5】 假定兩個獨立貸款項目在1年內均有0.02的概率損失1 000萬美元,同時均有0.98的概率損失100萬美元,任意一個單筆貸款在展望期為1年、97.5%的置信區間下的VaR為100萬美元,將兩個貸款疊加產生一個投資組合,組合有0.02×0.02=0.000 4的概率損失2 000萬美元,並且有2×0.02×0.98=0.039 2的概率損失1 100萬美元,有0.98×0.98=0.960 4的概率損失200萬美元。在展望期為1年、97.5%的置信度下,組合的VaR為1 100萬美元,單筆貸款所對應VaR的和為200萬美元,貸款組合的VaR比貸款VaR的總和高900萬美元,這違反了次可加性。
【例12-6】 我們考慮兩筆期限均為1年、本金均為1000萬美元的貸款。違約的概率由下表所示。

當其中任何一筆貸款違約時,收回本金的數量不定,但我們知道回收率介於0與100%的可能性為均等。當貸款沒有違約時,貸款盈利均為20萬美元。
首先考慮第一筆貸款,違約可能為1.25%,在違約發生的條件之下,損失均勻介於0與1 000萬美元,這意味著有1.25%的概率損失大於0;有0.625%的概率損失大於500萬美元;損失超出1 000萬美元的事件不會發生。損失超出200萬美元的概率為1%(在損失發生的前提下,有80%的概率損失會超出200萬美元,因為損失出現的概率為1.25%,損失大於200萬美元的無條件概率為0.8×0.012 5=0.01,即1%),因此,1年期的99%VaR為200萬美元。同樣的計算也適用於第二筆。
接下來考慮兩筆貸款的組合,違約出現的概率為2.5%。同上,違約所觸發的損失在0與1000萬美元之間均勻分佈。對應這種情況,VaR的估計值為580萬美元,這是因為在兩筆貸款之中有一筆貸款違約的概率為2.5%,在違約發生的條件下,損失超過600萬美元的可能性為40%。因此,損失大於600萬美元的無條件概率為2.5%×40%=1%。當一筆貸款產生違約時,另外一筆貸款會盈利20萬美元,將這一盈利考慮在內,我們得出1年的99%VaR為580萬美元。
將單獨計算的單一貸款所產生VaR相加,我們得出VaR的總和為200萬美元+200萬美元=400萬美元,將兩筆貸款組合在一起得出的VaR比單項VaR的總和580萬美元多180萬美元,這違反了次可加性條件(我們都知道將多筆貸款合成一交易組合會帶來風險分散的效應,但我們看到,兩個交易組合合併之後的VaR可能會大於兩個交易組合VaR的和)。
如果一個風險測度滿足以上所有的4個條件,則這樣的測度被稱為一致性風險測度。例12-5和例12-6說明,VaR不滿足一致性條件。我們可以證明以上討論的預期虧空測度滿足一致性條件,以下例子說明了這一點。
【例12-7】 讓我們考慮例12-5中的情形。每筆貸款的VaR均為100萬美元。為了計算在97.5%的置信區間下的預期虧空,我們注意到,在2.5%的尾部分佈中,有2%的概率損失為1 000萬美元,有0.5%的概率損失為100萬美元(注意,其他97.5%的分佈所對應的損失也為100萬美元),在2.5%的尾部分佈的範圍內,有80%的概率損失為1000萬美元,有20%的概率損失為100萬美元,損失的期望值(以百萬計)為0.8×10+0.2×1,即820萬美元。
將兩個貸款項目結合到一起時,在2.5%的尾部分佈中,有0.04%的概率損失為2 000萬美元,有2.46%的概率損失為1 100萬美元,在2.5%的尾部分佈的範圍內,損失的期望值為(0.04/2.5)×20+(2.46/2.5)×11,即1 114.4萬美元。
因為8.2+8.2>11.144(以百萬美元計),所以我們得出預期虧空滿足次可加性條件。
【例12-8】 考慮例12-6中的情形,我們已經展示了單筆貸款所對應的VaR為200萬美元,將展望期設為1年,在99%的把握之下所對應的預期虧空等於在損失大於200萬美元的條件之下損失的期望值。我們已知損失服從0~1 000萬美元的均勻分佈,如果損失大於200萬美元,那麼預期虧空為200萬美元與1000萬美元之間的中間值,即600萬美元。
例12-6說明,兩筆貸款組成的貸款組合的VaR為580萬美元,貸款組合的預期虧空等於在損失大於580萬美元的條件之下損失的期望值。當一筆貸款違約時,另一筆貸款不可能違約(這一點是由於假設),這時,貸款組合的價值介於20萬美元的盈利(+20)及980萬美元的損失(-980)之間的均勻分佈,損失介於580萬美元與980萬美元之間的期望值為780萬美元。因此,貸款組合的預期虧空為780萬美元。
因為7.8小於2×6(以百萬美元計),所以我們得出預期虧空滿足次可加性條件。
可加性條件並非只是一個理論要求,銀行不難發現,有時將兩個交易組合(例如,將股票交易組合和固定收益投資組合)疊加在一起時,疊加後的組合VaR會升高。
譜函數型風險測度
一個風險測度可以通過其分配給損失分佈的分位數的權重來描述。[3]VaR對第X個分位數設定了100%的權重,而對其他分位數設定了0權重;ES對高於第X個分位數的所有分位數設定了相同比重,而對低於第X個分位數的分位數設定了0比重。我們可以對於分佈中的其他分位數設定不同的比重,並以此定義出所謂的譜函數型風險測度(spectral risk measure)。當譜函數型測度分配給第q個分位數的權重為q的非遞減函數時,該測度一定滿足一致性條件(這種測度滿足次可加性條件)。ES滿足以上要求,但VaR並不滿足以上要求,因為VaR對於高於X的分位數所設定的權重小於對於第X個分位數所對應的權重。研究人員提出了其他形式的風險測度,在這些測度中,第q個分位數的權重隨著q的改變而有較大的變化,其中一種想法是使得第q個分位數所對應的權重與e-(1-q)/γ成比例,這裡的γ為常數,這種權重設定所對應的測度被稱為指數譜函數風險測度(exponential spectral risk measure)。圖12-5展示了當γ為兩種不同的值時,ES及指數譜函數風險測度所對應的不同權重。
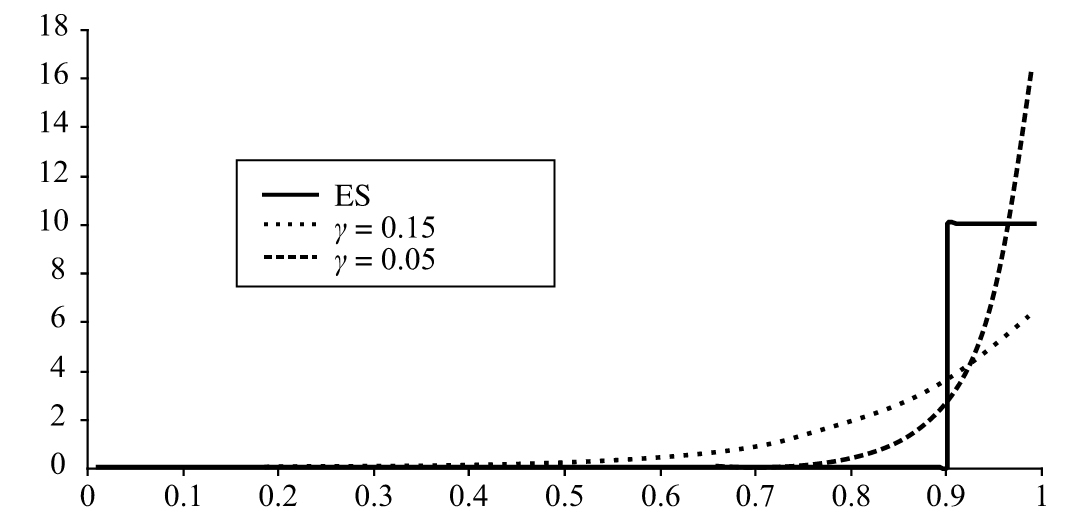
圖12-5 在3種情形中,權重作為分位數的函數
注:a)X=90%所對應的ES;b)γ=0.15所對應的指數譜風險測度;c)γ=0.05所對應的指數譜測度。
[1] See P. Artzner, F. Delbaen, J. -M. Eber, and D. Heath, “Coherent Measures of Risk,” Mathematical Finance 9(1999):203-228.
[2] 在組合規模不大時,這樣認為是沒有問題的。但當組合規模變得十分巨大時,其流動性就受到限制,相應地,資本金的要求可能也會提升。
[3] 這裡的分位數(quantiles)也被稱為百分位數(percentiles)或部分分位數(fractiles)。