e1 John Hull 風險管理與金融機構 v5
12.2 計算VaR的例子
在本節中,我們將提供VaR計算的4個例子,在前兩個例子中,收益(損失)分佈為連續形式;在後兩個例子中,收益(損失)分佈為離散形式。
【例12-1】 假定一個交易組合在6個月內的收益服從正態分佈,分佈均值為200萬美元,標準差為1000萬美元。從正態分佈的性質得出,分佈的第一個分位數為2-2.326×10即-2 130萬美元,因此,對於6個月展望期,在99%置信度下的VaR為2 130萬美元。
【例12-2】 假定一個1年項目的最終結果介於5 000萬美元損失和5 000萬美元收益,5 000萬美元損失和5 000萬美元收益之間的任意結果具有均等的可能,這時,項目的最終結果服從由-5 000萬美元到+5 000萬美元的均勻分佈,損失大於4 900萬美元的可能性為1%,因此,對於1年展望期,在99%置信度下的VaR為4 900萬美元。
【例12-3】 假定一個1年項目有98%的概率收益為200萬美元,1.5%的概率損失為400萬美元,0.5%的概率損失為1 000萬美元。損失累計分佈如圖12-3所示,在這一累計分佈下,對應於99%累計概率的點為400萬美元,因此,對於1年展望期,在99%置信度下的VaR為400萬美元。
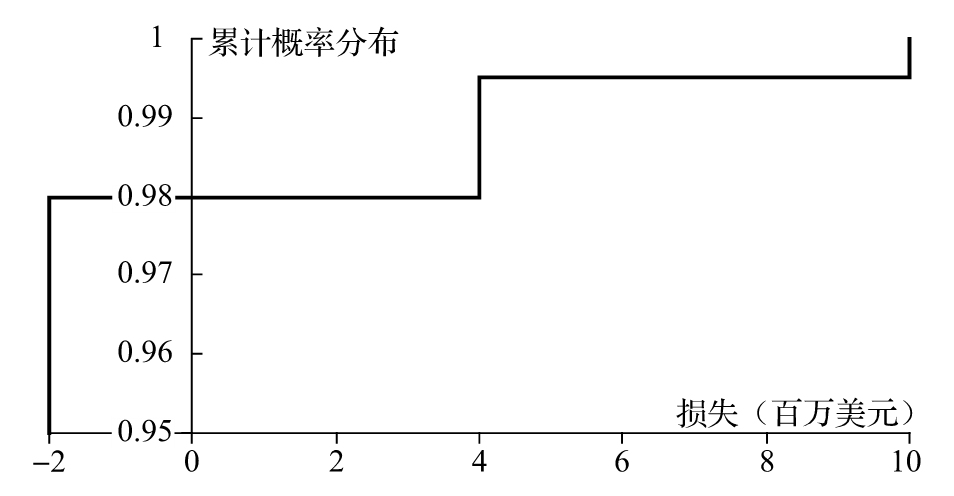
圖12-3 例12-3和例12-4中的累計損失分佈
【例12-4】 考慮例12-3中的情況,假定我們想求得對在99.5%置信度下的VaR,這時,圖12-3顯示,對介於400萬美元和1 000萬美元的任何一點的損失,均有99.5%的把握不會被超出。對於這一區間的任意數值V,損失超出V的概率均為0.5%。VaR在這一情形不具有唯一性,一個合理的選擇是將VaR設定為這一區間的中間值,這意味著,在99.5%置信度下的VaR為700萬美元。