e1 John Hull 風險管理與金融機構 v5
11.6 將Copula應用於貸款組合:Vasicek模型
在這裡我們將討論一元高斯Copula函數的一種應用,這對於我們理解第15章中的《巴塞爾協議Ⅱ》資本金要求中的公式會有幫助。假定一家銀行有一個鉅額的貸款投資組合。每個貸款每年的違約概率是1%。如果貸款違約是相互獨立的,則每年違約率的期望值大概是1%。但在實際中,貸款的違約不是相互獨立的,它們全都受宏觀經濟的影響。其結果是,在某些年,違約率會比較高,而在其他一些年份,違約率會比較低。表11-6通過統計1970~2016年的違約率證實了這種情況。違約率從1979年最低的0.088%到2009年最高的4.996%不斷變化。其他一些違約率比較高的年份有1970年、1989年、1990年、1991年、1999年、2000年、2001年、2002年、2008年和2016年。
表11-6 1970~2016年所有被評級的公司的年百分比違約率
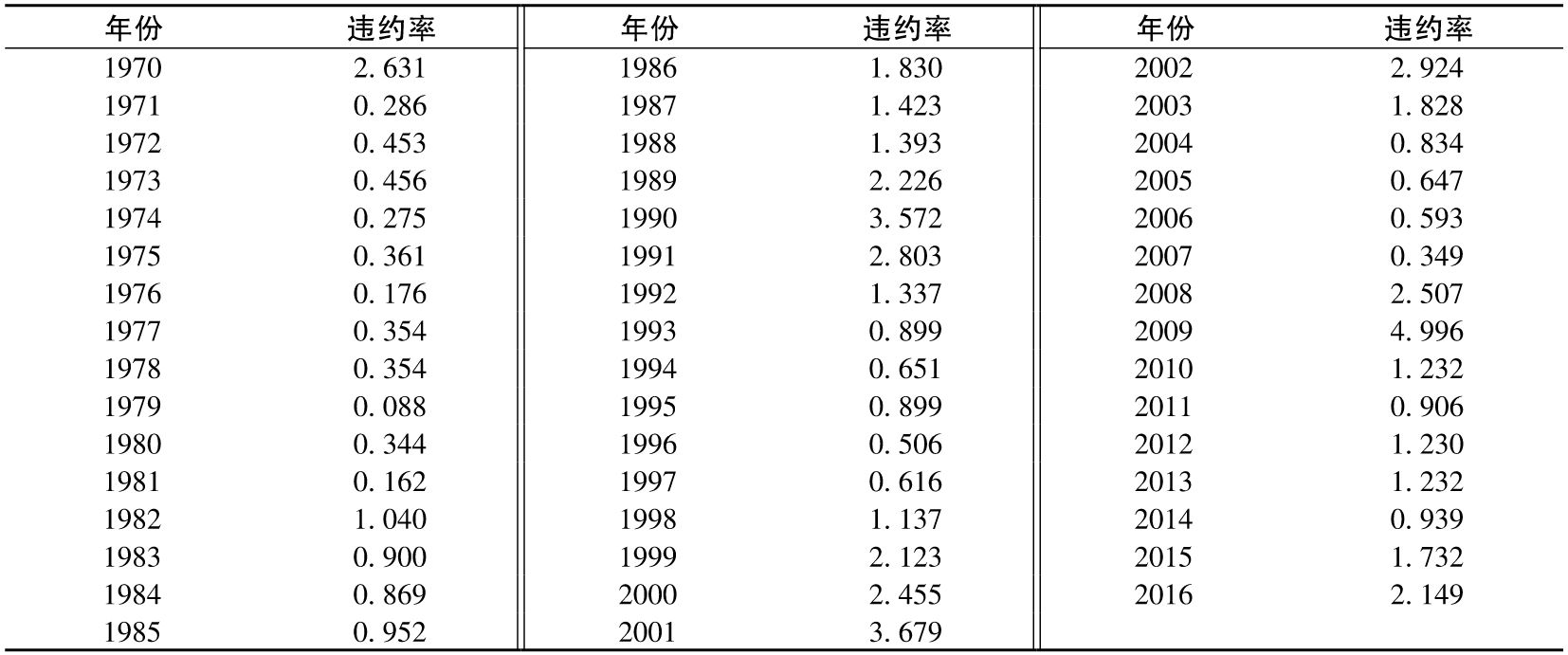
資料來源:穆迪。
為了給組合中貸款的違約率建立模型,定義Ti(1≤i≤N)為公司i的違約時間(這裡暗含的假設是,所有的公司在最終總會破產——只是違約發生的時間會在很久的將來,也許是在幾百年後)。在此我們對問題做一下簡化,假定所有貸款的違約時間的累積概率分佈函數相同,並定義PD為到時間T已發生違約的概率
PD=Prob(Ti<T)
高斯Copula模型可用來描述各貸款之間違約時間的相關結構。按照上面討論的步驟,對每一個i,我們將違約時間變量Ti的累積分佈的分位數與變量Ui的累積分佈的分位數之間進行一一對應的映射,這裡的Ui具有標準正態分佈。我們假定Ui之間的相關結構滿足式(11-8)中描述的因子模型,並且所有的ai都相等,記為a。於是有
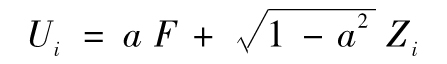
與式(11-8)一樣,變量F及Zi為相互獨立的正態分佈,Zi之間也相互獨立。在這種情況下,每對貸款之間的Copula相關性是相等的,均為
ρ=a2
於是,Ui可以記作

定義最壞情況下的違約率(worst case default rate)WCDR(T,X)為時間T內的違約率(即違約的貸款數與總貸款數的百分比),且該違約率有X%的概率不被超過(在很多情況下,T的時間跨度是1年)。根據我們的假設,我們會得到以下結論
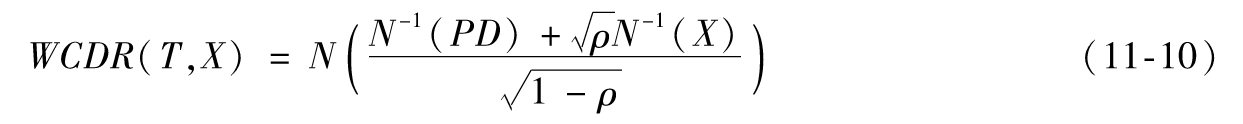
這個結果看上去有些奇怪,但它非常重要。Vasicek在1987最先得出了這個結果。[1]N和N-1是累積正態分佈函數和反累積正態分佈函數,它們可以很容易地由Excel計算表中的NORMSDIST和NORMSINV函數來計算。注意,如果ρ=0,那麼所有貸款的違約是相互獨立的,此時WCDR=PD。隨著ρ的增加,WCDR會隨著增加。
【例11-2】 假如一家銀行對大量零售客戶發放了大量貸款。每筆貸款的年違約概率為2%,在Vasicek模型中,Copula相關係數ρ的估測值為0.1,此時
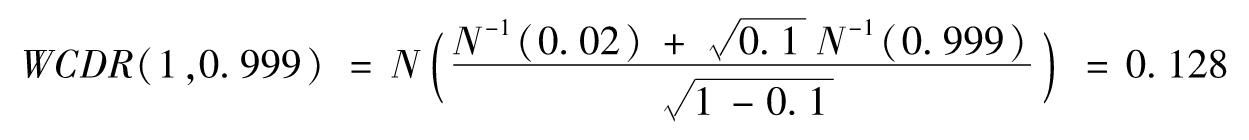
以上計算顯示我們有99.9%的把握肯定違約率不會大於12.8%。
11.6.1 對Vasicek結果的證明
根據高斯Coupula模型的性質,我們有
PD=Prob(Ti<T)=Prob(Ui<U)
其中
U=N-1[PD]
(11-11)
在式(11-9)中,到時間T時違約的概率依賴於因子F。該因子可以被理解成宏觀經濟指數。如果F比較高,則宏觀經濟形勢好,每個Ui趨向較高的值,對應的Ti的值也因此更高,這意味著,在較短時間內發生違約的可能性較低,所以Prob(Ti<T)的值也比較低。如果F比較低,則宏觀經濟形勢差,每個Ui及Ti趨向較小的值,所以在較短時間內發生違約的概率較高。為了進一步說明這一點,我們考慮給定F時違約的條件概率。
由式(11-9)可得出
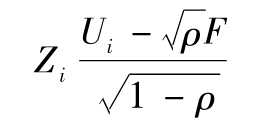
在因子F的值給定的條件下,Ui<U的條件概率為

以上概率與Prob(Ti<T|F)等同,因此
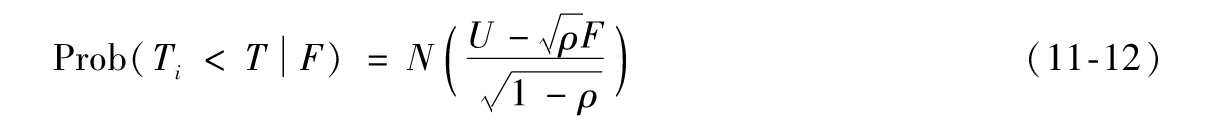
由式(11-11)
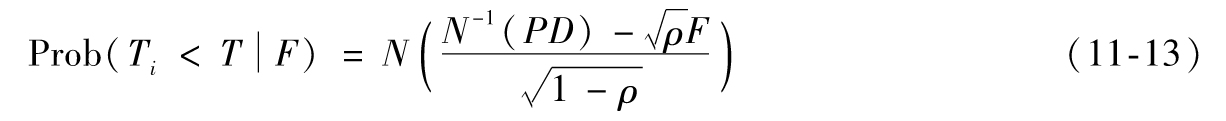
對於一個較大的貸款組合,如果各筆貸款具有相同的違約概率,並且每對貸款之間的Copula相關性為ρ,則以上表達式是對T時刻F條件下貸款組合違約百分比的一種很好的估計,我們將以上表達式定義為違約率(default rate)。
當F減小時,違約率會增加,那麼違約率最壞的狀況會是怎樣呢?F服從標準正態分佈,F<N-1(Y)的概率為Y,因此,存在一個概率Y,使得違約率大於
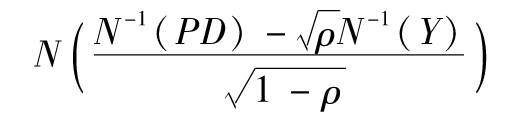
置信度為X%,展望期為T的情況下的違約率可以通過將Y=1-X代入以上表達式得到。因為N-1(X)=-N-1(1-X),所以我們可求得式(11-10)的值。
11.6.2 估計違約概率和相關性ρ
第10章介紹的最大似然估計法可以用來從歷史違約數據中估計違約概率和相關性ρ。我們可通過式(11-10)來計算違約率分佈的高分位數,但實際上,該式對所有的分位數都適用。如果DR為違約率,G(DR)為DR的累積概率分佈函數,由式(11-10)

將該式做變換,可得
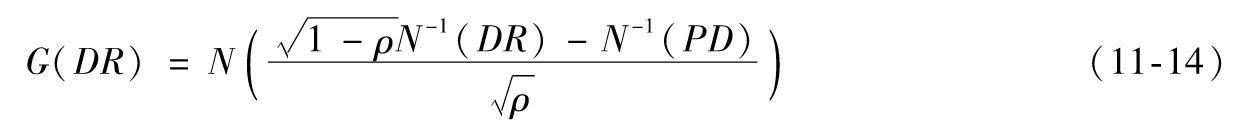
對該式求導,違約概率的概率密度函數為

由歷史違約數據計算違約概率PD和相關性ρ的最大似然估計的步驟如下:
(1)選擇PD和ρ的初始值;
(2)對DR的每個觀察值,計算式(11-15)中概率密度函數的對數;
(3)使用Solver搜索PD和ρ的值使得步驟(2)中各值的和最大。
對錶11-6中的數據使用上述步驟。對ρ和PD的最大似然估計值分別是0.098和1.32%(計算過程見作者的網站上提供的計算表)。違約率的概率分佈如圖11-6所示。第99.9%分位數對應的違約率為
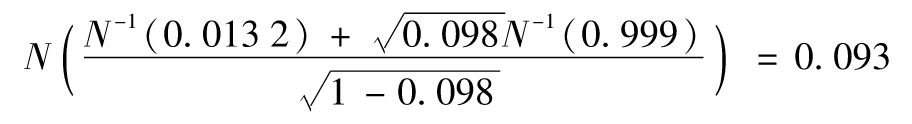
即每年9.3%。

圖11-6 違約率的概率分佈,參數由表11-6所示的數據得出
11.6.3 除高斯Copula以外的其他Copula函數
單因子高斯Copula模型有其侷限性。如圖11-4所示,其得出的尾部相關性很小。這意味著一家公司的意外提早違約和另一家公司的意外提早違約很少同時發生。要找到合適的ρ來擬合數據可能比較困難。例如,如果PD為1%而10年中某年的違約率達到3%,則找不到ρ的值可以跟這種情況保持一致。其他一些具備更強的尾部相關性的單因子Copula模型可以更好地擬合數據。
開發這樣一種模型的方法是為F或Zi選取比式(11-9)中的正態分佈具有更厚尾部的分佈(這些分佈要被放縮,以保證均值為0,標準差為1),然後Ui的分佈再由F和Zi的分佈(可能通過數值方法)決定。式(11-10)變為

其中,Φ、Θ和Ψ分別是Zi、F和Ui的累積概率分佈函數。此時,式(11-14)變為[2]
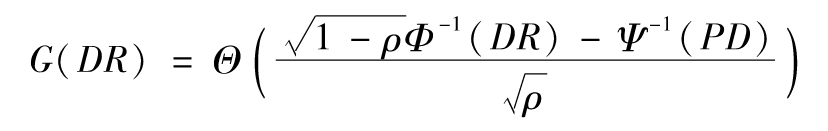
[1] See O. Vasicek, “Probability of Loss on a Loan Portfolio” (Working Paper, KMV, 1987).Vasicek的結果也發表在2002年12月期的Risk雜誌上,文章的標題為“Loan Portfolio Value”。
[2] 在論文“The Risk of Tranches Created from Mortgages”(J. Hull and A. White, Financial Analysts Journal 66, no.5 (September/October 2010):54-67)中,本方法被用於估計由房屋抵押貸款創造的分檔證券的風險。在很多情況下,此方法能更好地擬合曆史數據,但它的缺點在於其中使用的概率分佈相較正態分佈處理起來更復雜,有時需要使用數值方法來確定Ψ和函數g(DR)。