e1 John Hull 風險管理與金融機構 v5
11.5 Copula函數
考慮兩個相互關聯的變量V1和V2。V1的邊際分佈(marginal distribution,有時也被稱為無條件分佈)是指我們在對V2一無所知的情況下V1的概率分佈;類似地,V2的邊際分佈是指我們在對V1一無所知的情況下V2的概率分佈。假定,我們已經對V1和V2的邊際分佈有所估計,我們需要對相關結構做什麼樣的假設來決定變量之間的聯合分佈呢?
當V1和V2的邊際分佈均為正態分佈時,一種方便的做法是假設V1和V2服從二元正態分佈[1](見第11.3節關於相關性的討論)。對於其他邊際分佈,我們也可以做類似的假設。但是通常來講,對於兩個不同的邊際分佈,並沒有一個自然的方式定義相關結構,這就是我們需要引入Copula函數的原因。
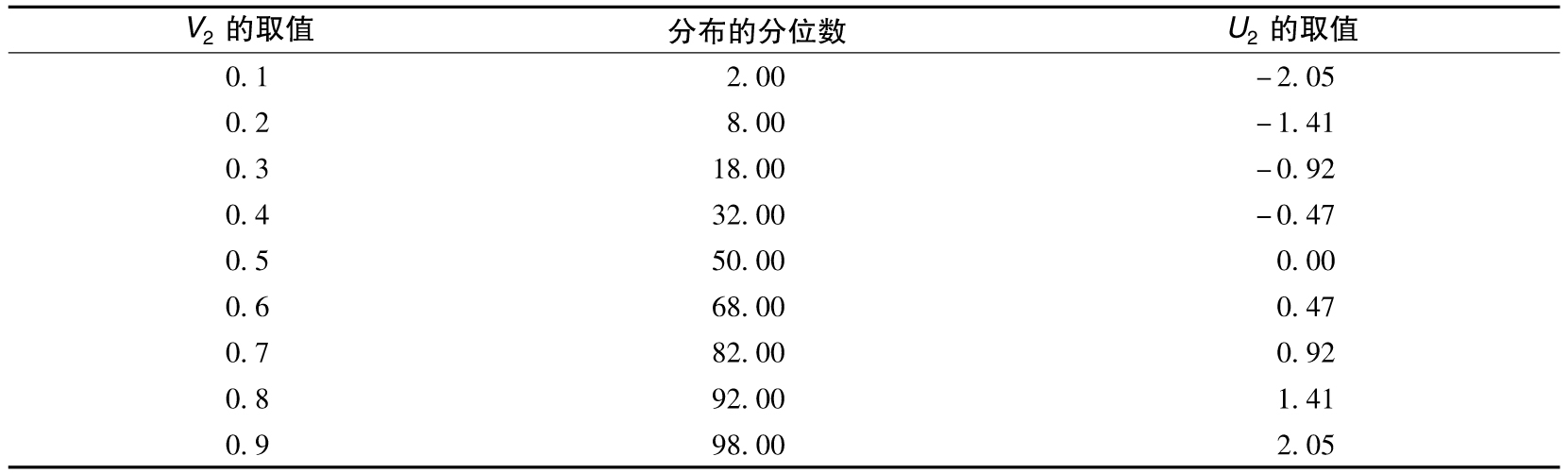
以下是一個有關Copula函數的應用的實例,假定V1和V2的邊際分佈為三角分佈,如圖11-2所示,兩個變量均介於0與1之間。V1分佈函數的峰值發生在0.2,V2分佈函數的峰值發生在0.5,兩個分佈函數的最大值均為2.0(因此兩個密度函數下的區域面積均為1.0)。為了應用高斯Copula(Gaussian Copula)函數,我們首先將變量V1和V2映射到U1和U2上,這裡的U1和U2均服從標準正態分佈。這種映射為分位數與分位數(percentile-to-percentile)之間的一一映射。V1分佈上1%的分位數被映射到U1分佈上1%的分位數;V1分佈上10%的分位數被映射到U1分佈上10%的分位數,等等。對於V2,我們也做類似的映射。表11-3顯示了V1的值如何被映射到U1上,表11-4顯示了V2的值如何被映射到U2上。在表11-3中,當V1=0.1時,對應於(求取三邊形面積)0.1的累積概率為0.5×0.1×1=0.05,即5%,V1=0.1的值被映射到標準正態分佈的5%的分位數,其值為-1.64。[2]

圖11-2 V1和V2服從某種三角分佈
表11-3 V1到U1的映射,V1服從圖11-2a中的三角分佈,U1服從標準正態分佈
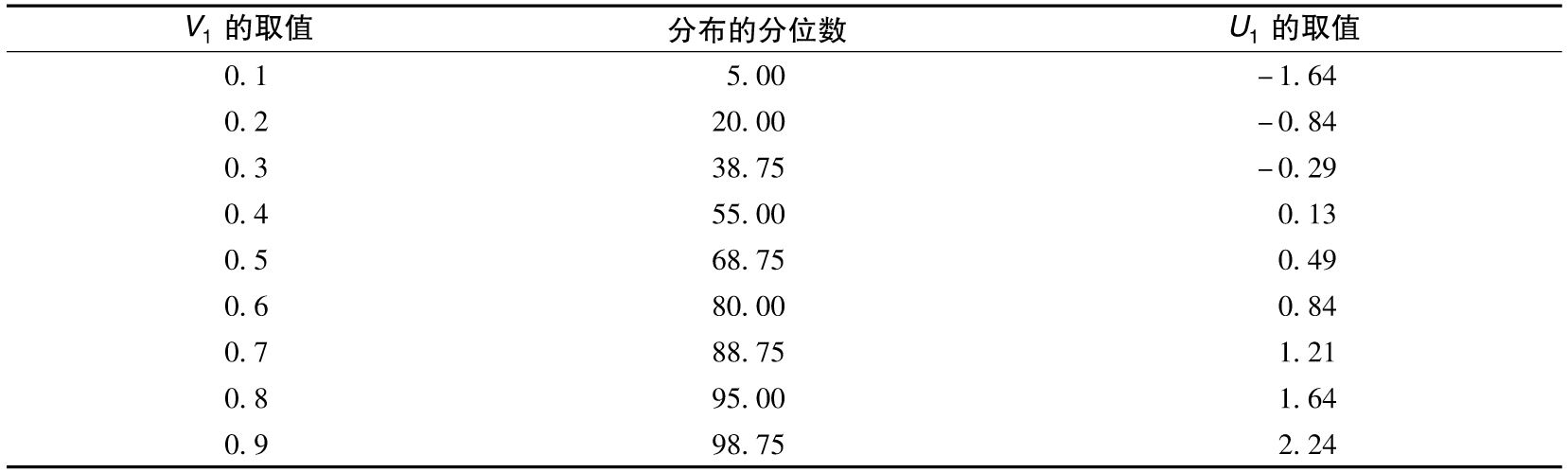
表11-4 V2到U2的映射,V2服從圖11-2b中的三角分佈,U2服從標準正態分佈
變量U1和U2服從正態分佈,我們假定U1和U2的聯合分佈為二元正態分佈,在這種前提下可以推算出V1和V2的聯合分佈以及相關結構。Copula函數的精髓就在於不直接定義V1和V2的相關性,而是採取一種間接的定義方式。我們將V1和V2映射到性狀較好(well-behaved)的分佈上,而對於這些性狀較好的分佈,我們可以較為容易地定義相關性。
假定U1與U2的相關係數為0.5。表11-5顯示出V1和V2的聯合累積概率分佈。為了說明計算過程,我們首先考慮如何計算V1<0.1和V2<0.1的概率。從表11-3及表11-4出發,我們知道這一概率與U1<-1.64和U2<-2.05的概率相同,通過二元正態分佈,我們可以得出在ρ=0.5的情形下,這一概率數值為0.006[3](在ρ=0的情形下,這一概率僅僅為0.02×0.05=0.001)。
表11-5 在高斯Copula函數模型下V1和V2的聯合概率分佈,相關係數=0.5,表中顯示出V1和V2分別小於某數值的聯合概率
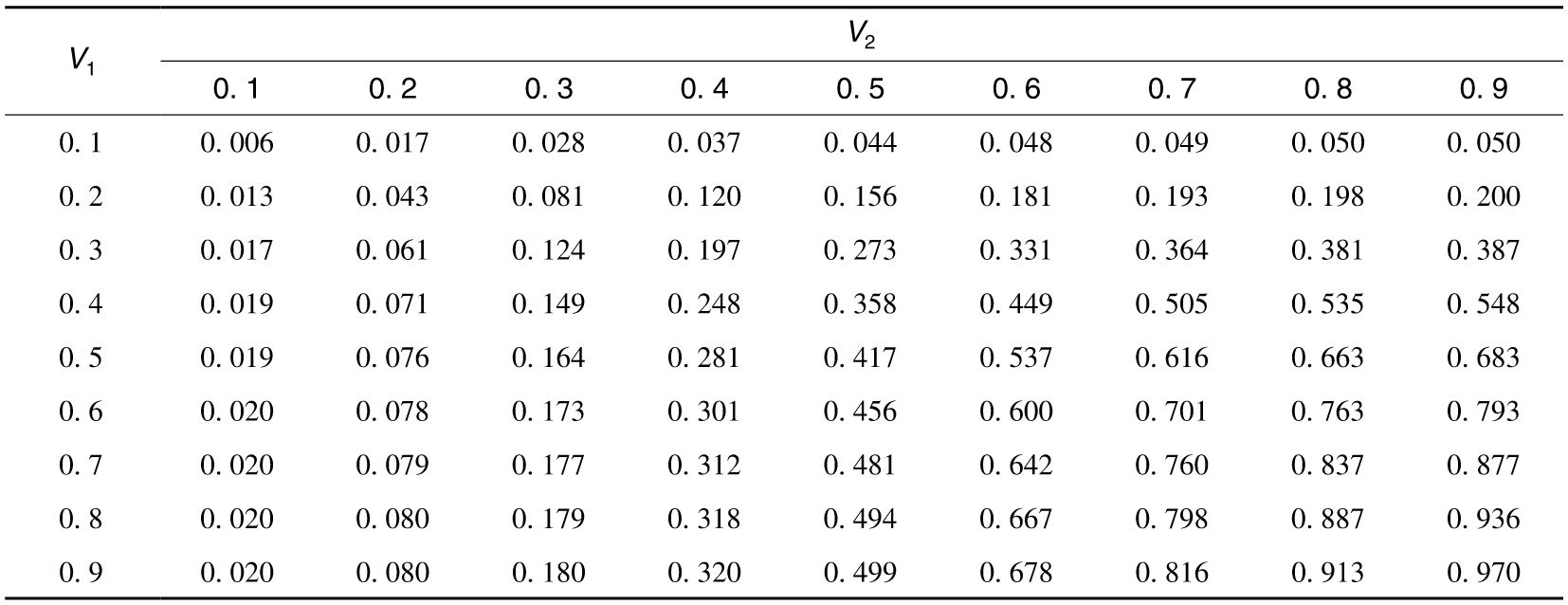
U1和U2的相關係數被稱為Copula相關係數。這一相關係數與通常意義下V1和V2的相關係數不同。U1和U2服從二元正態分佈,U2的條件期望值與U1有線性關係,U2的條件標準差為常數(在第11.4節中曾討論過),但是對於V1和V2,我們沒有類似的結論。
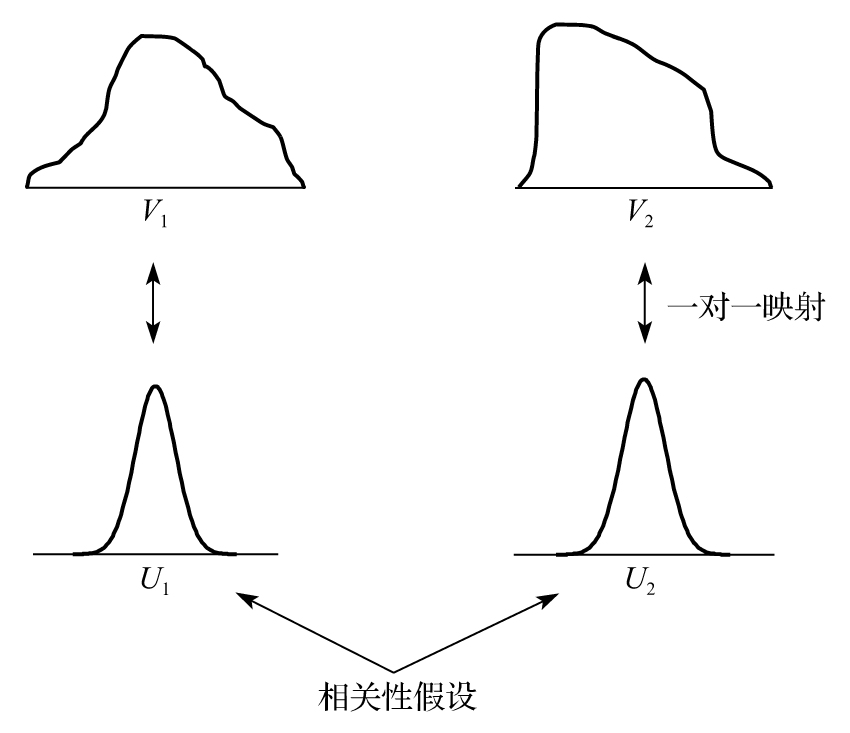
圖11-3 通過Copula函數來定義聯合分佈
11.5.1 Copula函數的代數表達形式
利用Copula模型來定義聯合分佈的方式可由圖11-3來說明。為了能夠以比較正規的形式來描述Copula函數,假定G1和G2分別為V1和V2的累積邊際(即無條件)概率分佈函數,我們將V1=v1映射到U1=u1,V2=v2映射到U2=u2,映射方式如下
G1(v1)=N(u1), G2(v2)=N(u2)
其中N代表累積正態分佈函數,這意味著
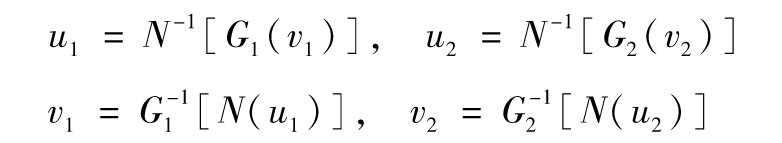
變量U1和U2被假設為服從二元正態分佈,Copula函數的主要特徵就是在定義其相關結構時,V1和V2的邊際分佈沒有任何改變(不管邊際分佈是何種形式)。
11.5.2 其他Copula函數
高斯Copula函數只是定義V1和V2相關性結構的某一種形式,還有許多其他的Copula函數可以用於描述相關性結構。其中一種Copula函數被稱為學生(student)t-Copula函數,這種Copula函數同高斯Copula函數類似,其不同之處只是U1和U2被假定為服從二元學生t-分佈。對於一個有f個自由度,相關係數為ρ的學生t-分佈進行模擬抽樣如下:
(1)在一個逆卡方分佈(inverse chi-square)中進行抽樣,抽樣值為χ(在Excel計算表中,我們可以採用CHIINV函數,第一個變量為RAND(),第二個變量為f);
(2)如第11.4節所述,在一個二元正態分佈中進行抽樣,這裡的相關係數為ρ;
(3)將正態分佈抽樣值乘以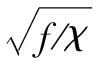 。
。
11.5.3 尾部相關性
圖11-4顯示了二元正態分佈的5000個抽樣。圖11-5顯示了二元學生t-分佈的5000個抽樣,這裡的相關係數均為0.5,學生t-分佈的自由度為4。定義尾部值(tail value)為一個分佈中最左邊或最右邊佔1%區域的尾部所對應的取值。在正態分佈抽樣中,大於2.33或小於-2.33的抽樣值為尾部值。類似地,在t-分佈抽樣中,大於3.75或小於-3.75的抽樣為尾部值,圖中的橫豎線顯示了產生尾部值的情形。圖形顯示在二元t-分佈中兩個變量同時出現尾部值的情形要多於在二元正態分佈中兩個變量同時出現尾部值的情形。換一種說法,二元t-分佈的尾部相關性(tail correlation)要大於二元正態分佈的尾部相關性。我們在前面提到,在極端的市場條件下,變量之間的相關性往往會增加,這說明圖11-1c對相關性的描述往往會比圖11-1a更好,基於這一結果,有些研究人員認為學生t-Copula對市場變量的相關性變化的描述比高斯Copula更好。
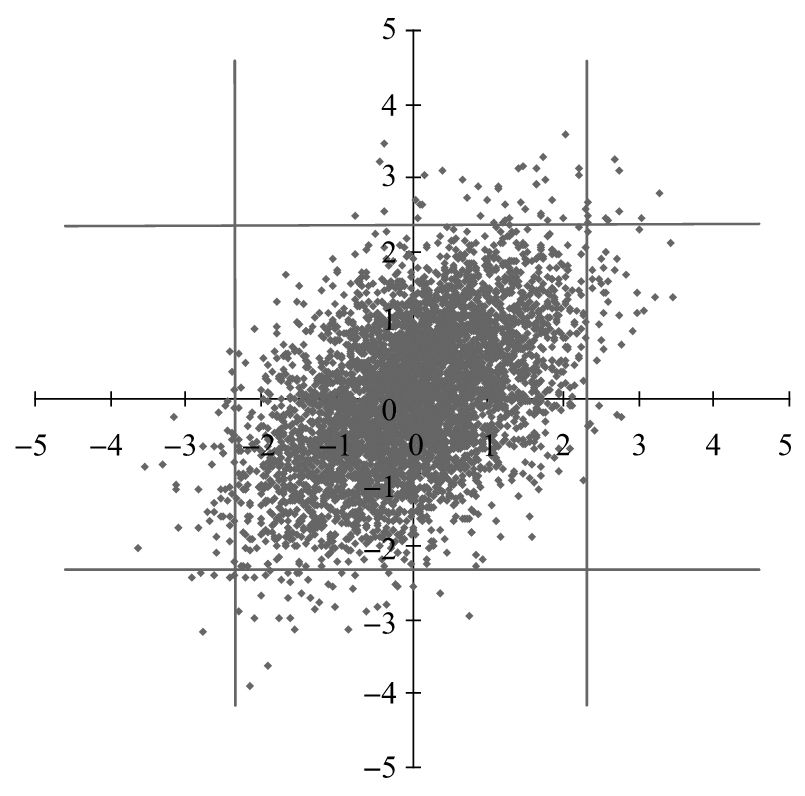
圖11-4 二元正態分佈的5 000個抽樣
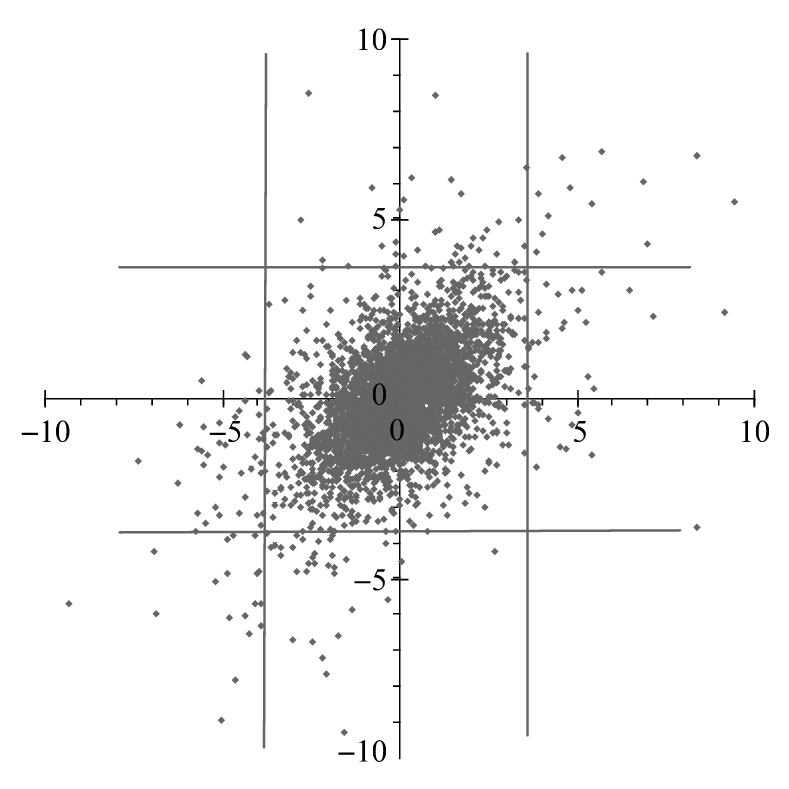
圖11-5 二元學生t-分佈的5 000個抽樣
11.5.4 多元Copula函數
Copula函數可以用於描述多於兩個變量之間的相關結構,其中最簡單的例子就是多元高斯Copula。假定我們已知N個變量V1,V2,…,VN的邊際分佈,對於任意變量i(1≤i≤N),我們將Vi映射到Ui,其中Ui服從標準正態分佈(這裡的映射是分位數之間的一一對應),我們最後假定Ui(1≤i≤N)服從多元正態分佈。
11.5.5 因子Copula模型
在多元Copula模型中,市場分析員常常假定變量Ui之間的相關性由某種因子來決定。在單一因子模型中,由式(11-6),我們得出

其中F和Zi分別服從標準正態分佈,Zi之間相互獨立,Zi與F之間也相互獨立。其他形式的因子Copula模型在選擇因子時也通常要保證F和Zi的期望值為0及標準差為1的條件。我們將在第11.6節中進一步討論與信用風險相關的問題。選擇不同的分佈會影響變量Ui之間的相關性,進而影響Vi變量之間的相關性。
[1] 儘管二元正態分佈是個比較方便的假設,但這一習慣性假設並不是唯一選擇。關於兩個服從正態分佈的變量,我們可以通過許多不同的方式來使得兩個變量相互關聯,例如,我們可以令V2=V1,對應於-k≤V1≤k的情形;V2=-V1,對應於其他情形。練習題11.11是另一個例子。
[2] 在Excel中可採用公式NORMSINV(0.05)=-1.64來計算。
[3] 在作者的網頁(www-2.rotman.utoronto.ca/~hull/riskman)上,讀者可以下載計算二元正態累積分佈函數的Excel計算表。