BUSINESS BOOKS

11.4　多元正態分佈

多元正態分佈很容易被理解及應用，在下一節中我們將解釋，多元正態分佈可以被用來描述變量之間的相關性結構，這甚至在每個單一變量不服從正態分佈時也可以做到。

我們首先假定兩個變量V₁和V₂服從二元正態分佈，假定變量V₁的某個觀察值為v₁，V₂在V₁=v₁條件下的分佈為正態分佈，期望值為

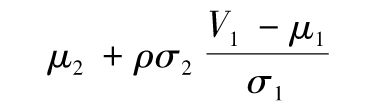
標準差為

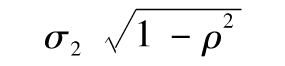
這裡的μ₁和μ₂分別為V₁和V₂的（無條件）期望值；σ₁和σ₂分別為V₁和V₂的（無條件）標準差，ρ為V₁和V₂的相關係數。注意V₂的條件期望值（條件為V₁）與V₁有線性關係，這對應於圖11-1a，V₂的條件標準差（條件為V₁）與V₁無關。

用於計算累積雙變量正態分佈的軟件位於作者的網站上：www-2.rotman.utoronto.ca/~hull/riskman。

11.4.1　基於正態分佈來產生隨機抽樣

在大多數計算機語言中都有產生介於0到1之間的隨機數的程序，許多語言也有產生服從正態分佈隨機數的能力。^[1]

當我們需要產生二元正態隨機變量的隨機抽樣ε₁、ε₂（兩個變量的均值均為0，方差均為1）時，我們可以採用如下流程：首先生成兩個服從標準正態分佈（即均值為0且標準差為1的分佈）並且相互獨立的隨機抽樣z₁和z₂，然後採用以下關係式來生成所需要的隨機抽樣

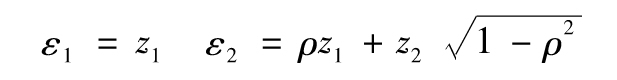
其中ρ為二元正態分佈的相關係數。

接下來我們考慮如何產生n元聯合正態分佈的隨機抽樣（其中所有變量的均值均為0，標準差均為1），這裡變量i與變量j的相關係數為ρ_ij。我們首先生成n個相互獨立並且服從正態分佈的隨機抽樣z_i（1≤i≤n）。服從n元聯合正態分佈的隨機抽樣可由下式產生

這裡參數α_ik的選取需要保證ε_j之間具有特定的方差和相關性。對於1≤j<i，我們有關係式

以及，對於所有的j<i

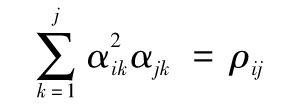
第一個變量的抽樣ε₁=z₁，所有的α變量可以通過對以上方程求解而得，其中ε₂由z₁、z₂求得，ε₃由z₁、z₂、z₃求得，等等。這裡描述的過程被稱為Cholesky分解（Cholesky decomposition）（見練習題11.9）。

如果我們在Cholesky分解中遇到對負數開根號，那麼最初的方差-協方差矩陣一定不滿足內部一致性條件，如同在第11.3.1節解釋的那樣，這就等於是說矩陣不滿足半正定條件。

11.4.2　因子模型

有時服從正態分佈的幾個不同變量的相關係數是由某個因子來決定的。假設U₁，U₂，…，U_N均服從標準正態分佈（期望值為0、標準差為1的正態分佈被稱為標準正態分佈），在單一因子模型中，每個U_i（1≤i≤N）均同一個共同的因子F及另外一個相互獨立的因子有關，準確地講

其中F及Z_i均服從標準正態分佈，a_i為介於-1與1之間的一個常數，Z_i（i=1，…，N）之間相互獨立，每一個Z_i同F也相互獨立。選擇Z_i的係數使得U_i的均值為0，方差為1。在單一因子模型中，U_i同U_j的相關性起源於共同因子F，變量U_i同U_j的相關係數為a_ia_j。

單因子模型（one-factor model）的優點是這一模型對於相關結構做了某種假設，使得協方差矩陣總是半正定。在沒有因子模型的前提下，我們必須對N個變量之間的相關性進行估計，這就造成我們需要估計N（N-1）/2個參數，而在因子模型的前提下，我們只需要估計a₁，a₂，…，a_N等N個參數。資本資產定價模型是投資行業單因子模型的一個例子，其中股票的回報包括單一市場變量和單一特殊變量，而這個特殊變量與其他股票回報相獨立，被稱為非系統變量（見第1.3節）。

單一因子模型可以被擴展到2個、3個甚至M個因子，在M個因子模型中

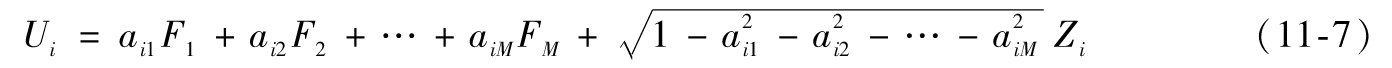
因子F₁，F₂，…，F_M服從標準正態分佈，並且相互獨立，因子Z_i之間相互獨立，並且每一個Z_i與所有的F因子也相互獨立，這時U_i與U_j的相關係數為

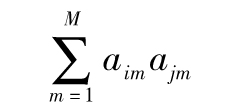
[1] 在Excel中，我們可以採用指令=NORMSINV(RAND())來達到這一目的。