e1 John Hull 風險管理與金融機構 v5
11.2 測量相關係數
在第10章中我們解釋瞭如何應用EWMA和GARCH模型來監測變量的方差，我們也可以採用類似的方法來監測兩個變量之間的協方差，一個變量每天變化的方差是指這一變量每天收益的方差。類似地，兩個變量每天變化的協方差是指變量每天收益的協方差。
假定變量X和Y在第i天結束時的價值為Xi和Yi，變量X和Y在第i天的收益率為
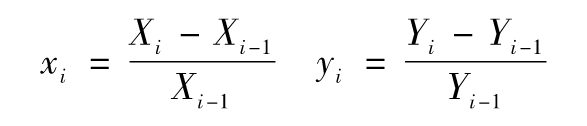
由式（11-2），我們得出變量X和Y在第n天的協方差為
covn=E（xnyn）-E（xn）E（yn）
在第10.5節中我們曾指出風險管理人員在計算每天方差率時常常假定變量的每天預期收益為0，風險管理人員在計算每天協方差時通常需要做出同樣的假設，這意味著變量X和Y在第n天的協方差可以被簡化為
covn=E（xnyn）
對於xi和yi的最近m個觀察值採用同樣的權重，我們得出
採用同樣的權重來估計變量X和Y的每天變化的方差，我們得出關係式
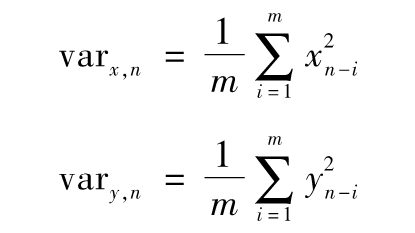
第n天的相關係數的估計值為
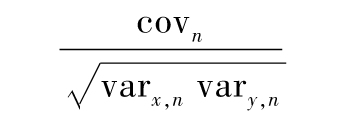
11.2.1 EWMA模型
大多數風險管理人員都同意早期歷史數據的權重應該小於近期歷史數據的權重。在第10章中我們曾討論過應用EWMA模型來預測方差，其中我們看到權重隨著回望期的期限的增大而按指數形式下降，對於協方差，我們可以採用類似的權重形式，一種更新協方差的EWMA模型與式（10-8）相似
covn=λcovn-1+（1-λ）xn-1yn-1
與EWMA模型中的分析相似，我們可以證明對應於數據xn-1yn-1的權重隨著i的增加（也就是隨著回望期的增大）而逐漸降低，λ的值越小，對於近期數據的權重也越大。
【例11-1】 假設λ=0.95，變量X和Y在n-1天的相關係數估計為0.6，同時我們假設變量X和Y在n-1天的波動率估計分別為1％和2％。由協方差及相關係數的關係式，在第n-1天的協方差估計值為
0.6×0.01×0.02=0.000 12
假定變量X和Y在n-1天的百分比變化分別為0.5%和2.5%。在第n天方差及協方差的估計分別為
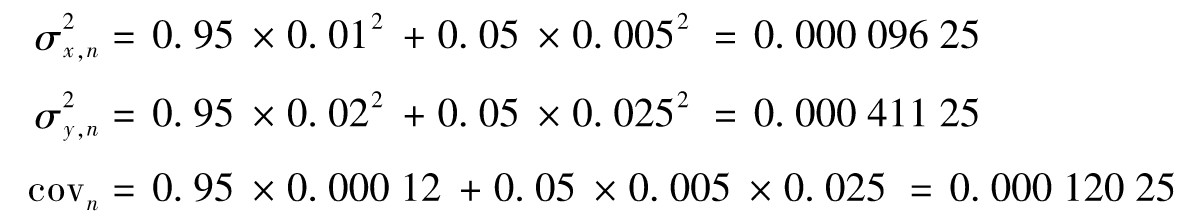
變量X的最新波動率估計值為
，變量Y的最新波動率估計為
，X和Y的最新相關係數為
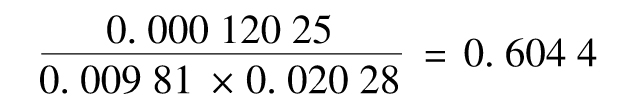
11.2.2 GARCH模型
GARCH模型也可以被用來更新協方差以及預測將來協方差的水平。例如，GARCH（1，1）更新X和Y協方差的表達式為
covn=ω+αxn-1yn-1+βcovn-1
這一公式同更新方差的式（10-10）相似，此公式對於長期平均協方差賦予某種權重，對於最新協方差估計賦予某種權重，對於最新觀測到的協方差數據（也就是xn-1yn-1）也賦予某種權重，長期平均協方差為ω/（1-α-β）。我們可以推導出類似式（10-14）和式（10-15）的表達式來預測未來的協方差，並且計算對應一個未來期限內的平均協方差。