e1 John Hull 風險管理與金融機構 v5
11.1 相關係數的定義
變量V1及V2的相關係數ρ被定義為
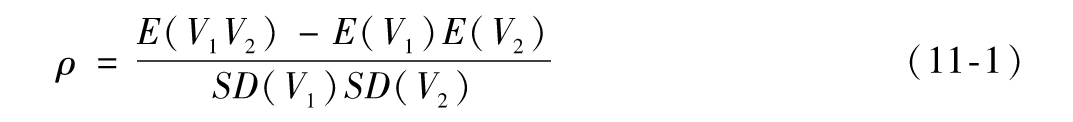
其中E(·)代表期望值,SD(·)代表標準差。如果兩個變量不相關,即E(V1V2)=E(V1)E(V2),因此ρ=0。如果V1=V2,以上表達式中的分子及分母均等於變量V1的方差,此時就像我們期望的那樣ρ=1。
變量V1及V2的協方差被定義為
cov(V1,V2)=E(V1V2)-E(V1)E(V2)
(11-2)
因此相關係數又可以寫為
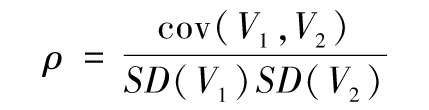
雖然直覺上我們更容易理解相關係數,但是在今後我們將說明協方差才是我們真正需要分析的變量,這類似於第10章的EWMA及GARCH模型,雖然波動率更容易被人理解,但方差才是真正的基礎變量。
相關係數以及關聯性
如果在兩個變量中,其中任意一個變量的信息(觀測值)不會影響另一個變量的分佈,那麼這兩個變量在統計上被定義為相互獨立。精確地講,如果對於所有的x,等式
f(V2|V1=x)=f(V2)
成立,其中f(·)代表變量的概率密度函數,|代表條件概率,變量V1和V2在統計上被定義為相互獨立。
如果兩個變量的相關係數為0,就意味著變量毫無關聯嗎?答案是否定的。這裡舉一個簡單例子來說明問題,假定變量V1的值有三種均等的可能:-1、0及+1。當V1=-1或V1=+1時,V2=1;當V1=0時,V2=0。在這裡我們可以清楚地看到V1和V2有某種關聯性,如果我們觀測到V1的值,我們也可得出V2的值,同時有關V2的信息也會改變我們有關V1的概率分佈。但由於E(V1V2)=0以及E(V1)=0,我們很容易驗證V1及V2的相關係數為0。
這一例子強調相關係數只是用於表達變量之間的某種相關性。這種相關性只是一種線性的關聯關係,而變量之間可以有許多不同形式的關聯關係。我們可以畫出E(V2)與V1的函數圖來顯示V1和V2的關聯特性。圖11-1顯示了幾種不同的關聯形式,圖11-1a顯示了V2的期望值同V1之間有某種線性關係,圖11-1b顯示了V2的期望值同V1之間有一種V形關聯關係(這同我們前面的例子相似,一種對稱的V形的高度關聯關係會造成相關係數為0),圖11-1c顯示了我們經常看到的金融變量之間的關聯性。在這裡V1和V2代表某些市場變量的變化率。當V1正常變化時,V1和V2之間有很弱的關聯性,但V1的極端變化會觸發V2的極端變化(這和市場受壓時,相關性會增加的情況是一致的)。
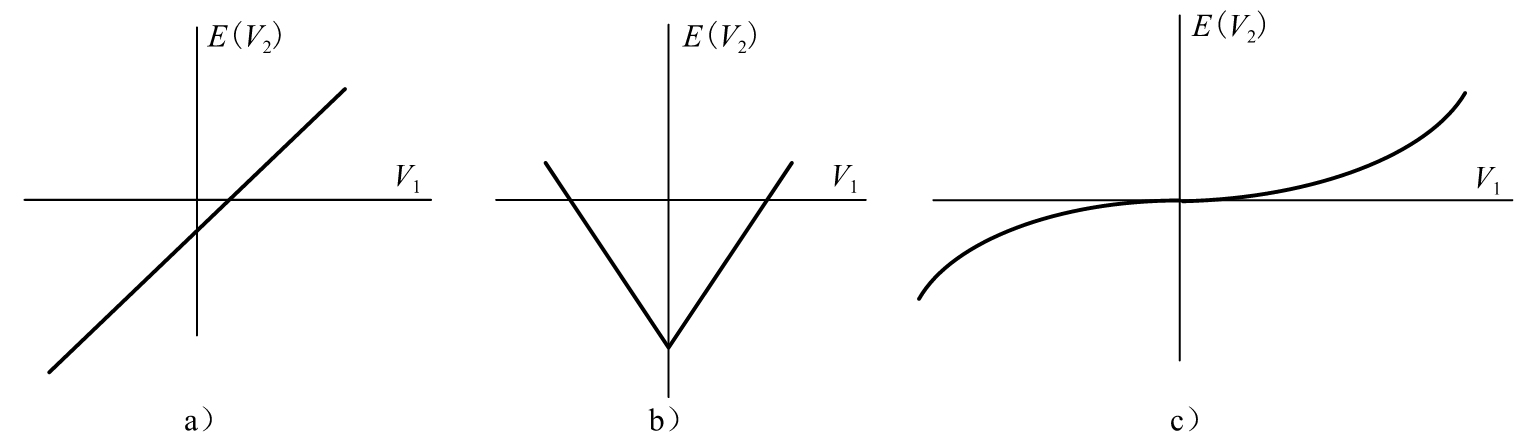
圖11-1 V2依賴於V1的幾種不同形式
我們可以從另一個角度來考察V1和V2的關聯性,即通過檢驗在V1條件下,V2的方差。我們在今後將看到,當V1和V2服從二元正態分佈時,該條件標準差為常數,但在其他情形下,V2的標準差與V1有關。