e1 John Hull 風險管理與金融機構 v5
作業題
10.18 假定股票在過去連續15天的價格(以美元計)為30.2,32.0,31.1,30.1,30.2,30.3,30.6,30.9,30.5,31.1,31.3,30.8,30.3,29.9,29.8。請用式(10-2)和式(10-4)估計股票價格波動率。
10.19 假定某資產價格在昨天收盤時為300美元,日波動率為1.3%,今天該資產的收盤價為298美元。請採用以下模型來更新波動率:
(a)採用EWMA模型,其中λ=0.94;
(b)採用GARCH(1,1)模型,其中參數選擇為ω=0.000 002、α=0.04以及β=0.94。
10.20 在本書作者的網頁(www-2.rotman. utoronto.ca/~hull/data)上,讀者可以下載一個Excel計算表,其中含有超過900天的不同匯率數據以及股指價格數據。選定某匯率及某種股指,估計EWMA中的λ以使得
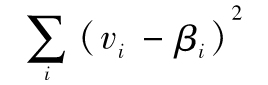
達到最小,其中vi為在i-1天天末對於方差所做的預測,βi是由第i天至第i+25天的數據所計算出的方差,在計算中請採用Excel中的Solver功能,在開始EWMA計算時,令第一天方差的預測值等於第一天收益的平方。
10.21 GARCH(1,1)模型中的參數α=0.03、β=0.95以及ω=0.000 002:
(a)長期平均波動率為多少?
(b)如果當前波動率為每天1.5%,你對20天、40天及60天后的波動率預估為多少?
(c)應採用什麼樣的波動率來計算20天、40天及60天期限的期權價格?
(d)假定有某一事件使得日波動率由1.5%增至2%,請估測這一事件對20天、40天及60天后波動率的影響。
(e)估測這一事件對用於20天、40天及60天期限的期權定價中的波動率的影響。
10.22 使用2005年7月27日~2010年7月27日的歐元兌美元匯率的歷史數據,估算EWMA和GARCH(1,1)模型的參數。數據可以從作者的網頁上下載:www-2.rotman.utoronto.ca/~hull/data。
10.23 投資組合在1個月後損失超出1 000萬美元的概率大約為5%:
(a)假定投資組合價值變化服從正態分佈,均值為0,1個月展望期置信度99%的VaR[1]為多少?
(b)在α=3的冪律假設前提下,1個月展望期置信度99%的VaR為多少?
[1] VaR的概念將在本書第12章中介紹。——譯者注