BUSINESS BOOKS

小結

在風險管理中，日波動率被定義為每天市場變量的百分比變化的標準差。每天的變化的方差為每天波動率的平方。波動率在交易日要遠高於在非交易日，因此在波動率計算過程中非交易日可以被忽略。每天的市場變化服從正態分佈這一假設很吸引人，但事實並非如此。大多數市場變量變化比正態分佈有更肥的尾部，因此冪律是對我們在日常生活中所遇到的許多分佈的尾部的一個更好的描述。冪律常常被用於描述許多市場百分比變化的尾部分佈。

本章描述瞭如何跟蹤及更新波動率的方法。我們定義u_i為第i-1天天末到第i天天末市場變量的百分比變化，市場變量的方差（即波動率的平方）為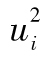的加權平均。這裡討論的模型的一個主要特性是對應於不同的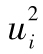，模型賦予不同的權重。數據越新，所對應的權重也越大。在EWMA及GARCH（1，1）模型中權重隨著回望期長度以指數速度下降。GARCH（1，1）與EWMA模型的不同之處在於GARCH（1，1）給長期平均方差也賦予了某種權重。EWMA及GARCH（1，1）模型的構造都保證了我們能夠較為容易地預測將來方差的水平。

最大似然法通常被用於估計GARCH（1，1）以及其他基於歷史數據來計算波動率的模型中的參數，這些方法採用數值迭代過程來確定參數，使得歷史數據得以出現的可能性達到最大。當參數確定之後，我們可以從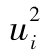中的自相關性是否被有效地剔除這一指標來驗證模型的好壞。

我們可以採用GARCH（1，1）模型由歷史數據估算期權波動率，這種分析常常被用於計算波動率的擾動對不同期限期權的隱含波動率帶來的影響。