BUSINESS BOOKS

10.10　採用GARCH（1，1）模型來預測波動率

採用GARCH（1，1）模型，在n-1天結束時所估算的第n天的方差為

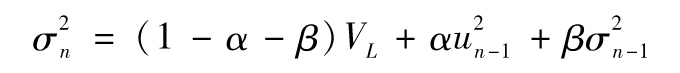
因此

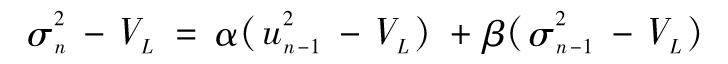
在將來第n+t天，我們有

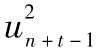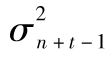的期望值為，因此

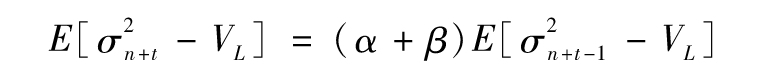
其中E表示期望值。連續應用該式，我們得出

或者

上式採用了在n-1天結束時的所有數據來預測第n+t天的波動率。在EWMA模型中，α+β=1。式（10-14）說明，將來方差的期望值與當前方差相等。當α+β<1時，式中最後一項隨時間增加而逐漸減小。圖10-6顯示出當前方差與V_L不同時，預期方差的將來路徑。如上所述，方差具備均值迴歸的性質，均值迴歸水平為V_L，迴歸速度為1-α-β。我們對將來方差的預測，會隨著展望時間的延長逐漸趨向於V_L，這一分析強調了為保證GARCH（1，1）模型的穩定，我們必須有α+β<1這一條件。當α+β>1時，對應於長期平均方差的權重為負，這時方差不具備均值迴歸特性，事實上，此時的模型具備均值逃離（mean fleeing）特性。

在前面考慮的標準普爾500指數數據中，α+β=0.993 5，V_L=0.000 207 5。假定我們對於當前方差的估計為每天0.000 3（這對應於日波動率為1.732%），10天之後的方差期望值為

0.000 207 5+0.993 5¹⁰×（0.000 3-0.000 207 5）=0.0002942

預期波動率為每天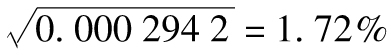，這一數值仍然高於長期日波動率（1.44%），但是500天后的預期方差為

0.000 207 5+0.993 5⁵⁰⁰×（0.000 3-0.000 207 5）=0.0002110

預期波動率為每天1.45%，這同長期波動率已經非常接近。

10.10.1　波動率期限結構

假定今天為第n天，定義

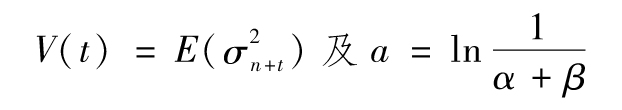
式（10-14）變為

V（t）=V_L+e^-at［V（0）-V_L］

這裡的V（t）是對今後第t天的即時方差（instantaneous variance）的估計，介於今天與時間T之間的日方差平均值為

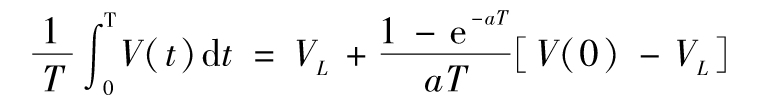
隨著期限T的增大，以上數值會更接近V_L。定義σ（T）為GARCH（1，1）模型對於一個期限為T天的期權定價時所採用的每年波動率，假定每年有252天，σ（T）²是每天方差的252倍，因此

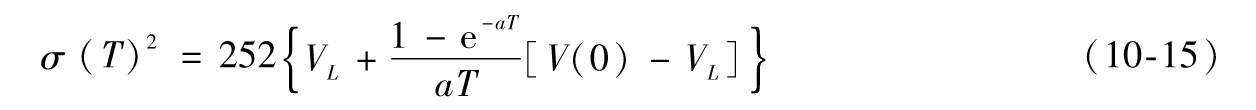
期權的波動率和期權期限之間的關係被稱作波動率期限結構（volatility term structure）。波動率期限結構通常用隱含波動率來求得，但是式（10-15）提供了另外一種途徑，即用GARCH（1，1）來估算。儘管由此所估計的期限結構同隱含波動率的期限結構會有所不同，但這種方法常常被用來預測真正的波動率期限結構如何對波動率的變化做出反應。

在當前波動率高於長期波動率時，GARCH（1，1）模型預測出的波動率期限結構為下降型（downward-sloping），而在當前波動率低於長期波動率時，GARCH（1，1）預測出的波動率期限結構為上升型（upward-sloping）。對標準普爾500指數的實例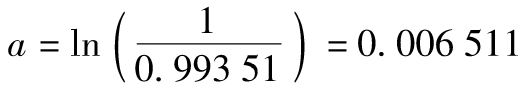，，V_L=0.000 207 5。假定當前的日方差估測為V（0）=0.000 3，由式（10-15）得出

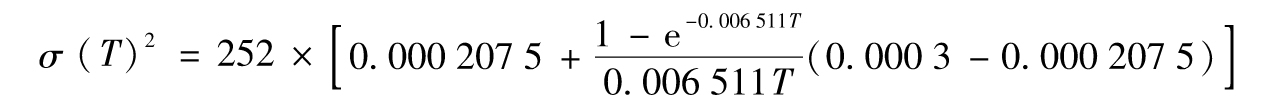
其中時間T以天計。表10-6顯示出對應於不同時間T的每年波動率。

10.10.2　波動率變化的作用

式（10-15）可以寫為

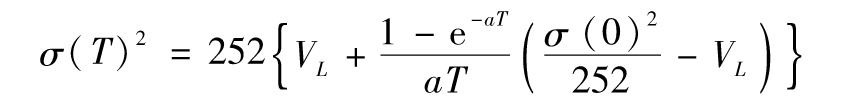
當σ（0）的變化量為Δσ（0）時，相應σ（T）的變化量約為

表10-7顯示了在標準普爾500指數例子中的波動率的變動對於不同期限的期權價格的影響。類似以前的假定，V（0）=0.000 3，因而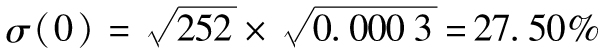。表中考慮的情形為即時波動率上升100個基點，由27.50%變為28.50%，這意味著Δσ（0）=0.01，即1%。

許多金融機構採用這樣的分析來確定其交易戶頭對於波動率變化的敏感性。在計算vega時，我們不是將所有期限的隱含波動率都增加1%，而是將波動率的變化量與期權期限的長短聯繫起來。在表10-7中，10天期權的波動率增加量為0.97%，30天期權的波動率增加量為0.92%，50天期權波動率增加量為0.87%，等等。