e1 John Hull 風險管理與金融機構 v5
10.9 最大似然估計法
現在是個很好的時機討論如何應用歷史數據來估計我們以上討論模型的參數,將要討論的方法被稱為最大似然法(maximum likelihood method)。在參數估算過程中,這一方法會涉及選擇合適的參數以使得產生所觀測到的數據的概率達到最大。
為了解釋這個方法,我們引用一個簡單的例子,隨機地抽取某一天10只股票的價格,我們發現其中一隻股票的價格在這一天下降了,而其他9只股票的價格或有所增加或至少沒有下跌,這裡我們要問,當天一隻股票價格下降的概率最好估計為多少?答案是0.1,讓我們看一下這一結果是否就是最大似然估計所給出的結果。
將任意股票價格下降的概率計為p,對應只有一隻股票價格下降,而其他股票價格不下降的概率為p(1-p)9(p對應於一只股票的概率,而其他9只股票中任意一隻股票不下降的概率為1-p),應用最大似然估計法,最好的估計值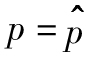 [1]是會使得p(1-p)9取得最大值。將以上表達式對p求導,並令導數為0,我們得出
[1]是會使得p(1-p)9取得最大值。將以上表達式對p求導,並令導數為0,我們得出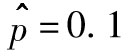 時會使得表達式取得最大值,這說明最大似然估計值正如期望的那樣為0.1。
時會使得表達式取得最大值,這說明最大似然估計值正如期望的那樣為0.1。
10.9.1 估計常數方差
在下一個有關最大似然估計法的例子中,我們考慮如何由服從正態分佈,並且期望值為0的變量X的m個觀察值來估計這一變量的方差。我們假定觀察值為u1,u2,…,um,其對應的期望值為0,將方差記為v。觀察值出現在X=ui的概率等於X的概率密度函數在ui的取值,即
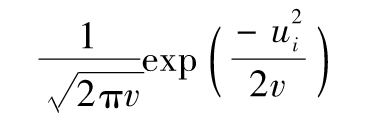
m個觀察值正好為u1,u2,…,um的概率為

應用最大似然法,v的最好估計使得以上表達式達到最大值。
以上表達式的最大化與其對應的對數最大化等價,對式(10-11)取對數並且忽略常數項,我們得出將被最大化的目標函數為

或
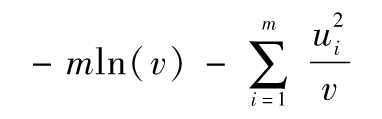
將以上表達式對v求導,並令導數為0,我們可以看到v的最大似然估計量為
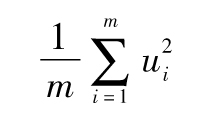
最大似然估計正是式(10-4)的估計式,而獲得無偏差估計值只需要將m替換為m-1。
10.9.2 估計GARCH(1,1)或EWMA模型中的參數
我們現在考慮如何用最大似然法來估計EWMA、GARCH(1,1)或其他波動率的方法中的參數。定義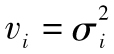 為第i天的方差的估計。假設在方差給定的條件下,ui的條件概率分佈為正態分佈。與上一節類似,我們得出最佳匹配參數應使得以下表達式最大化
為第i天的方差的估計。假設在方差給定的條件下,ui的條件概率分佈為正態分佈。與上一節類似,我們得出最佳匹配參數應使得以下表達式最大化
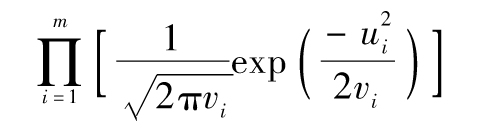
對這一表達式取對數,得出以上表達式最大化與以下表達式最大化等價

除了v被代替為vi,這一表達式與式(10-12)相同,我們可以採用迭代法來求取使得以上表達式達到最大化的解。在模型中迭代地尋找能最大化表達式(10-13)的參數很有必要。
表10-4中所示的計算表顯示出GARCH(1,1)模型中的參數估算過程,這一表格採用了2005年7月18日~2010年8月13日標準普爾500指數的數據。[2]
表中報告的數字是對GARCH(1,1)模型中3個參數ω、α及β的估計,表中第1列對應於日期,第2列對應天數,第3列顯示了在第i天結束時的標準普爾500指數價格Si,第4列顯示了由第i-1天結束時至第i天結束時價格的百分比變化,即ui=(Si-Si-1)/Si-1,第5列是對在第i-1天天末所做的第i天的方差的估計,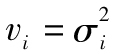 。對於第3天,我們將方差設為
。對於第3天,我們將方差設為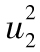 。在接下去的每一天,我們採用式(10-10)來估計方差,第6列顯示了可能性測度
。在接下去的每一天,我們採用式(10-10)來估計方差,第6列顯示了可能性測度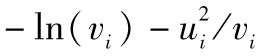 。第5列及第6列中的值是基於參數ω、α及β的當前值計算得出的。我們的目標是如何選取ω、α及β以使得第6列的和達到最大值,這一過程涉及迭代搜索。[3]
。第5列及第6列中的值是基於參數ω、α及β的當前值計算得出的。我們的目標是如何選取ω、α及β以使得第6列的和達到最大值,這一過程涉及迭代搜索。[3]
表10-4 使用2005年7月18日~2010年8月13日標準普爾500指數數據估計GARCH(1,1)模型中的參數
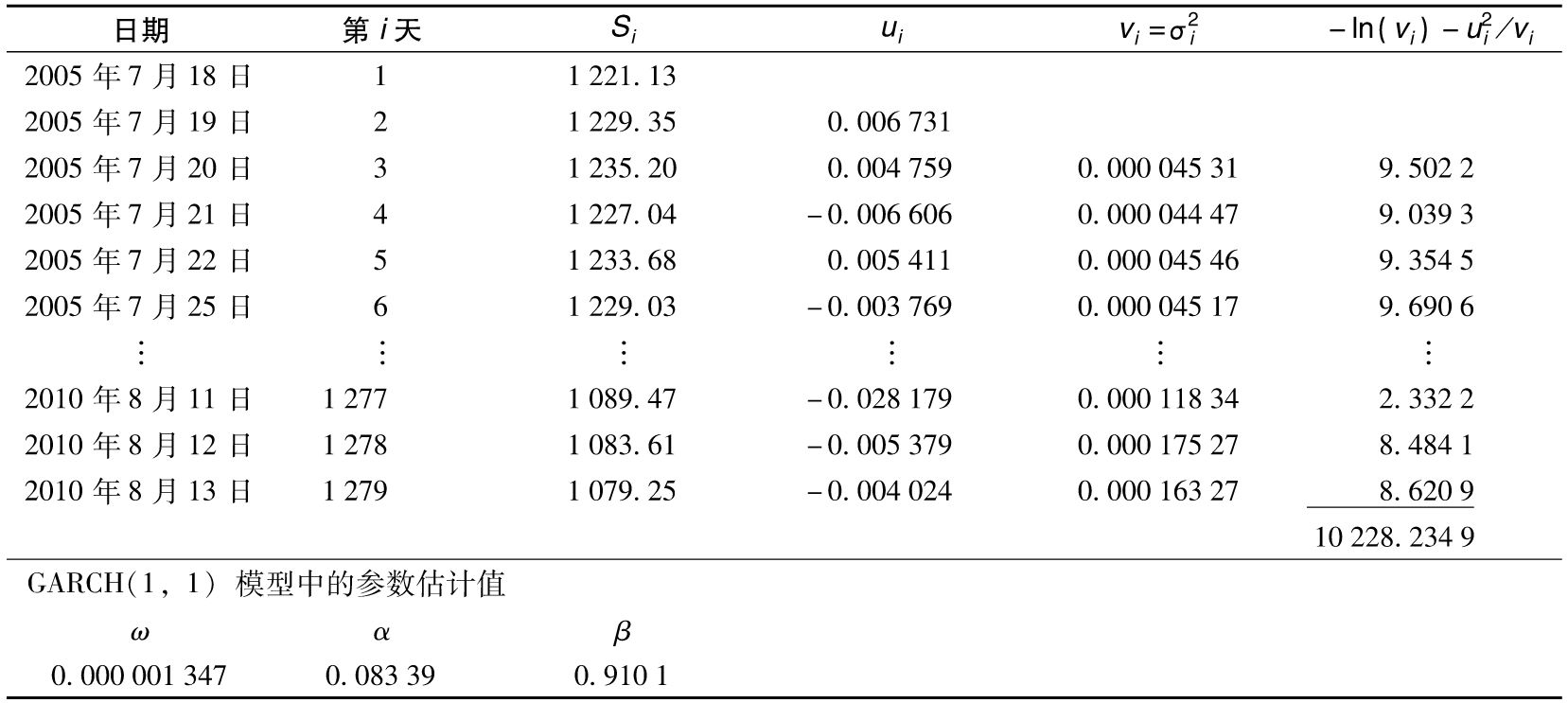
在我們的例子中,參數對應的最佳解為
ω=0.000 001 346 5, α=0.083 394, β=0.910 116
式(10-13)的最大值為10 228.234 9(在表10-4中所顯示的數字對應於參數ω、α及β的最終迭代解)。
在我們的例子中,長期方差VL為
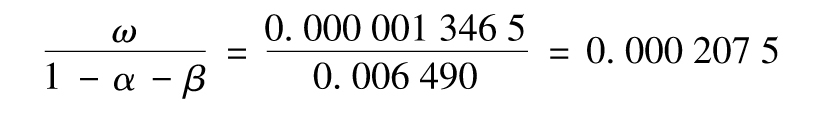
長期波動率為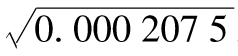 ,也就是每天1.440 4%。
,也就是每天1.440 4%。
圖10-4和圖10-5顯示了該數據涵蓋的5年期內的標準普爾500指數以及由GARCH(1,1)所計算的波動性。在大多數時間,每天的波動率小於2%,但在金融危機期間,某些天的波動率超過了5%(同期VIX指數也顯示了較高的波動率,參見圖10-1)。
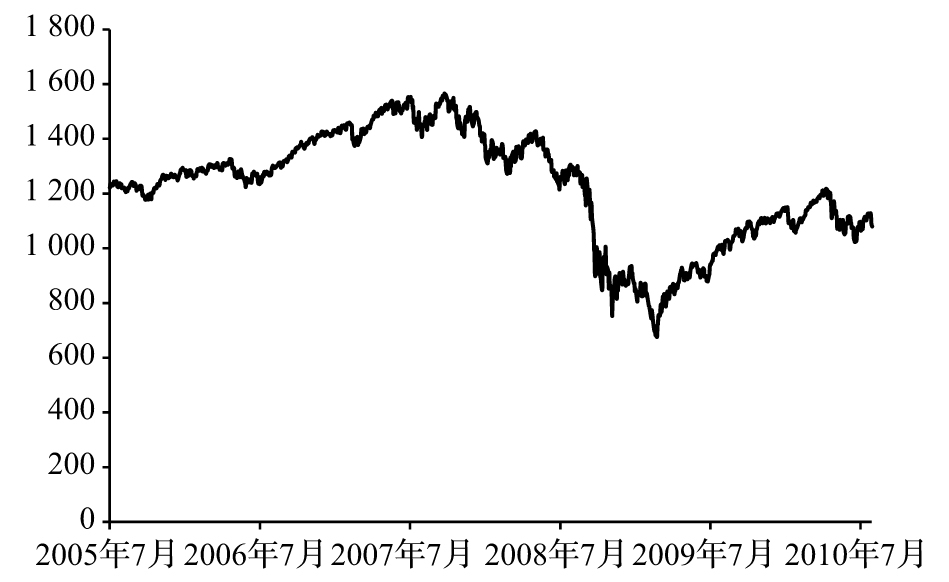
圖10-4 標準普爾500指數,2005年7月18日~2010年8月13日
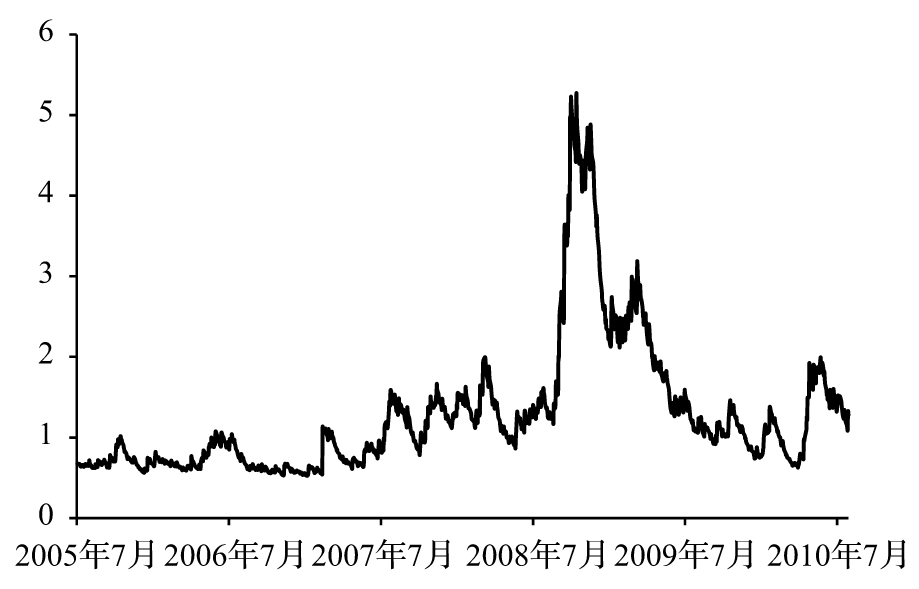
圖10-5 標準普爾500指數的GARCH(1,1)日波動率,2005年7月18日~2010年8月13日
估計GARCH(1,1)參數的另外一種更穩健的方法是所謂的方差目標法(variance targeting)。[4]這種方法將長期平均方差VL設定為由數據計算出的抽樣方差(或其他合理的估計)。因為ω的值等於VL(1-α-β),所以模型只需要估測兩個參數。表10-4的數據所對應的抽樣方差為0.000 241 2,每天的波動率為1.553 1%。令VL等於抽樣方差,我們可以找出使得目標函數式(10-13)達到最大化的α及β,分別為0.084 45和0.910 1,相應的目標函數取值為10 228.194 1,這一數字只是稍稍低於前面計算的極值數據10 228.234 9。
EWMA模型的參數估計過程就相對簡單一些,令ω=0、α=1-λ及β=λ,我們只需要估計一個參數λ,應用表10-4中的數據,使得目標函數式(10-13)取得最大值的λ為0.937 4,對應的目標函數取值為10 192.510 4。
GARCH(1,1)及EWMA模型方法均可以通過Excel軟件中的Solver程序實現,應用Solver,我們可以尋求使得似然函數達到最大的數值解。當計算表格中所尋求的數值解大體在同一水平時,Solver程序的表現令人滿意。例如,在GARCH(1,1)模型中,我們可以將計算表中的單元格A1、A2、A3與數據ω×105、10α及β相對應。然後我們可以使得單元格B1=A1/100 000、B2=A2/10以及B3=A3,我們用B1、B2、B3進行計算,但是讓Solver求解A1、A2、A3的數值以使得似然函數達到最大。偶爾,Solver可能會給出一個局部最優解,因此,有必要多試幾個不同的初始值。
10.9.3 模型表現如何
GARCH模型假設波動率的變化與時間有關。在某一階段波動率較高,而在其他階段波動率較低。換句話說,當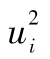 較高時,
較高時,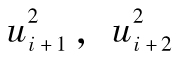 ,…也會較高;當
,…也會較高;當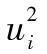 較低時,
較低時,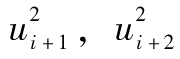 ,…也會較低,我們可以通過計算
,…也會較低,我們可以通過計算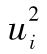 的自相關係數來檢驗這些結論的正確性。
的自相關係數來檢驗這些結論的正確性。
假定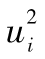 確實有自相關性,如果GARCH模型有效,那麼自相關性就會被剔除。我們通過計算變量
確實有自相關性,如果GARCH模型有效,那麼自相關性就會被剔除。我們通過計算變量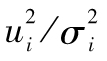 的自相關係數來驗證這一結論,如果計算出的結果顯示自相關性非常小,那麼我們就可以得出結論:有關σi的模型確實解釋了
的自相關係數來驗證這一結論,如果計算出的結果顯示自相關性非常小,那麼我們就可以得出結論:有關σi的模型確實解釋了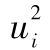 中的自相關性。
中的自相關性。
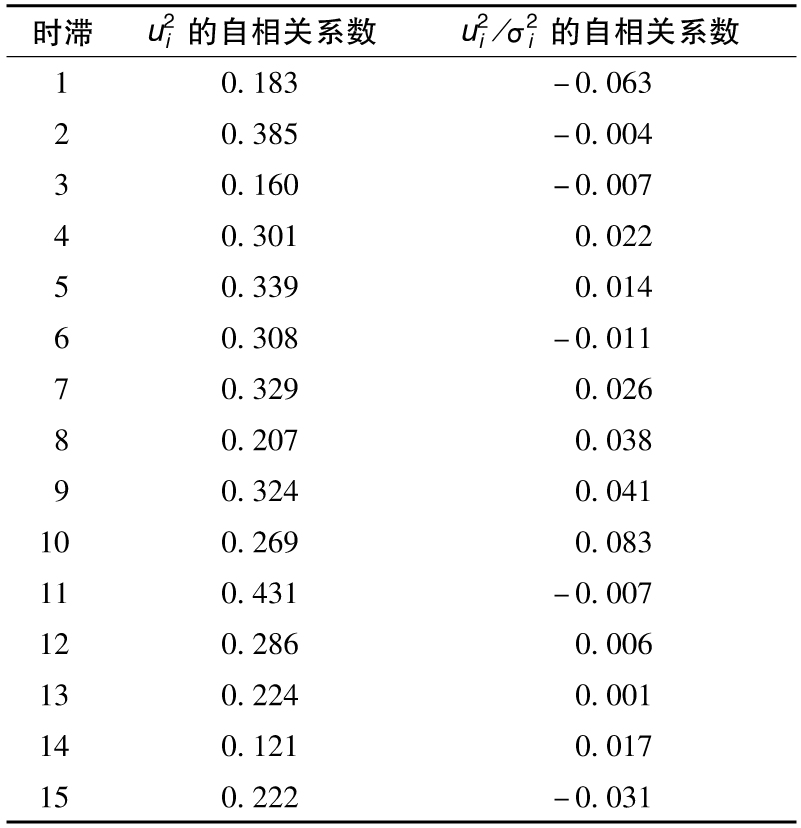
表10-5顯示的結果是基於以上的標準普爾500指數數據。第1列顯示了計算自相關係數所用的時滯(time lag),第2列對應於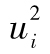 自相關係數,第3列展示了
自相關係數,第3列展示了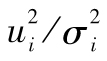 的自相關係數。[5]表中結果顯示出對應於1與15之間的所有時滯,
的自相關係數。[5]表中結果顯示出對應於1與15之間的所有時滯,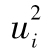 的自相關係數為正,而對於
的自相關係數為正,而對於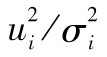 ,有些自相關係數為正,有些為負,這些相關係數的幅度比最初
,有些自相關係數為正,有些為負,這些相關係數的幅度比最初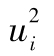 的相關係數要小。
的相關係數要小。
看來GARCH模型對於解釋數據確實做了很好的工作。如果想做一個更科學的檢驗,我們可以採用所謂的Ljung-Box統計方法。[6]當一個數列中有m個觀察值時,Ljung-Box統計量定義為
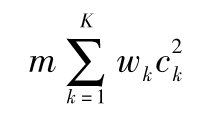
其中ck對應於時滯為k的自相關係數,K為所考慮的所有時滯,再有
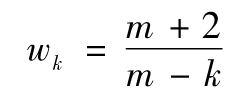
對應於K=15,當Ljung-Box統計量大於25時,我們可以有95%的把握拒絕自相關係數為0這一假設。
基於表10-5中數據,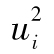 序列的Ljung-Box統計量為1566,這說明自相關性確實存在。關於數列
序列的Ljung-Box統計量為1566,這說明自相關性確實存在。關於數列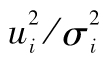 ,Ljung-Box統計量為21.7,這說明GARCH模型確實基本上剔除了數據中的自相關性。
,Ljung-Box統計量為21.7,這說明GARCH模型確實基本上剔除了數據中的自相關性。
表10-5 在採用GARCH模型之前以及之後的自相關係數
[1] 這裡的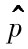 代表估計值,原書採用的符號為p。——譯者注
代表估計值,原書採用的符號為p。——譯者注
[2] 數據和計算過程可以在以下網站上找到:www-2.rotman.utoronto.ca/~hull/riskman。
[3] 就像在後面會討論的那樣,微軟軟件Excel中的廣義求解算法Solver可以用來對問題求解。
[4] See R. Engle and J. Mezrich, “GARCH for Groups,” Risk (August 1996):36-40.
[5] 數列xi對應於時滯k的自相關係數等於xi與xi+k的相關係數。
[6] See G. M. Ljung and G. E. P. Box, “On a Measure of Lack of Fit in Time Series Models,” Biometrica 65(1978):297-303.