e1 John Hull 風險管理與金融機構 v5: 10.7 GARCH（1，1）模型

e1 John Hull 風險管理與金融機構 v5

10.7　GARCH（1，1）模型

我們現在討論由Bollerslev在1986年提出的GARCH（1，1）模型。^[1]GARCH（1，1）模型與EWMA模型的不同類似於式（10-5）與式（10-6）的不同。在GARCH（1，1）中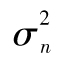，是由長期平均方差V_L、u_n-1及σ_n-1計算得出的，GARCH（1，1）表達式為

其中γ為對應於V_L的權重，α為對應於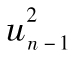的權重，β為對應於的權重，因為權重之和為1，我們有

γ+α+β=1

EWMA模型是GARCH（1，1）模型對應於γ=0、α=1-λ及β=λ的特例。

GARCH（1，1）模型中的“（1，1）”代表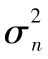是基於最近的u²的觀察值以及最新的方差的估計而得到的。在廣義的模型GARCH（p，q）中的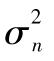是從最近p個u²的觀察值及q個最新的有關方差的估計而計算得到的。^[2]到目前為止，GARCH（1，1）是最流行的一種GARCH模型。

令ω=γV_L，我們可以將GARCH（1，1）模型寫成

這種模型的表達形式是為了估計參數。當ω、α及β被估算出後，我們可由γ=1-α-β來計算γ，長期方差V_L=ω/γ。為了保證GARCH（1，1）模型的穩定，我們要求α+β<1，否則對應於長期方差的權重會為負值。

【例10-8】　假設某一個由每天觀測數據估算出的GARCH（1，1）模型為

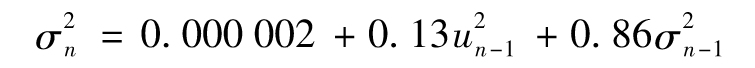
這對應於α=0.13、β=0.86以及ω=0.000 002。γ=1-α-β=0.01，ω=γV_L，得出V_L=0.000 2。換句話講，由模型隱含出的長期平均日方差平均為0.000 2，對應的波動率為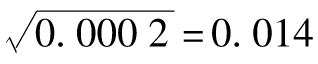，即每天1.4%。

假設對應於n-1天的日波動率估算值為1.6%，因此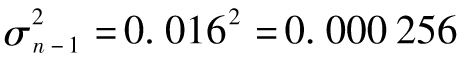，又假設n-1天市場價格降低1%，即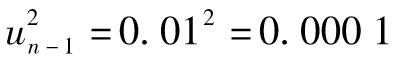，因此

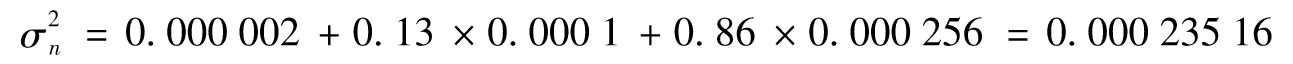
對於波動率的最新估計為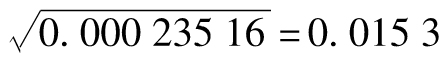，即每天1.53%。

權重

對式（10-10）中的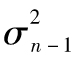進行替換，我們可得

即

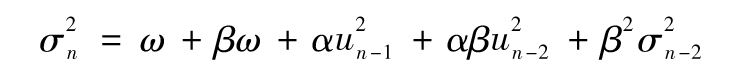
替換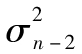，我們得到

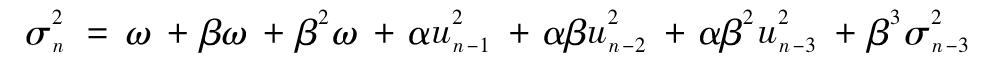
以這種形式繼續下去，我們可以看到對應於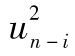的權重為αβ^i-1，權重以β指數速度下降，參數β可被解釋為衰減速度（decay rate），這與EWMA中的λ係數近似。在決定最新方差時，此係數決定了不同u_i的重要性。例如，如果β=0.9，說明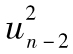的重要性只是的重要性的90%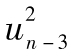，的重要性只是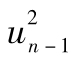的重要性的81%，依此類推。GARCH（1，1）與EWMA模型類似，其不同之處是在對過去的u²賦予指數衰減權重的同時，對於長期平均波動率也賦予了某種權重。

[1] See T. Bollerslev, “Generalized Autoregressive Conditional Heteroscedasticity,” Journal of Econometrics 31(1986):307-327.

[2] 有人已經提出反映公司非對稱信息的GARCH模型，在這些模型設計中，σ_n與u_n-1的符號有關。在某種意義上，這些模型比GARCH（1，1）更適合股票，這是因為股票的波動率常常與價格有反向關係，因此一個符號為負的u_n-1比一個符號為正的u_n-1對於σ_n的影響更大。關於處理非對稱信息的模型，讀者可參考D. Nelson, “Conditional Heteroscedasticity and Asset Returns: A New Approach,” Econometrica 59(1990):347-370 and R. F. Engle and V. Ng, “Measuring and Testing the Impact ofNews on Volatility,” Journal of Finance 48(1993):1749-1778。