e1 John Hull 風險管理與金融機構 v5: 10.6 指數加權移動平均模型

e1 John Hull 風險管理與金融機構 v5

10.6　指數加權移動平均模型

指數加權移動平均模型（EWMA）是式（10-5）的一個特殊形式，其權重α_i隨著回望時間的加長而按指數速度遞減。這一模型的特殊形式為α_i+1=λα_i，其中λ是介於0與1之間的某一常數。在以上特殊假設下，更新波動率的公式變得非常簡潔

第n天波動率σ_n（在第n-1天天末估算）由第n-1天波動率σ_n-1（在第n-2天天末估算）及最近一天價格變化率u_n-1的數據來決定。

為了說明式（10-8）的權重以指數速度下降，我們將式（10-8）所算出的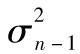代回式（10-8）之中

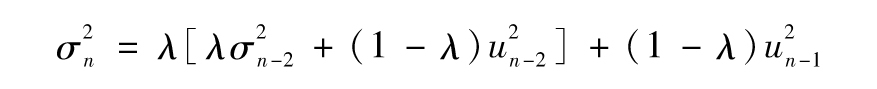
即

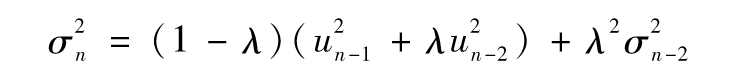
代入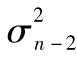項，我們進一步得出

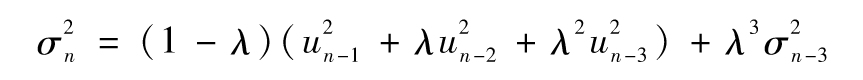
依此類推，我們得出

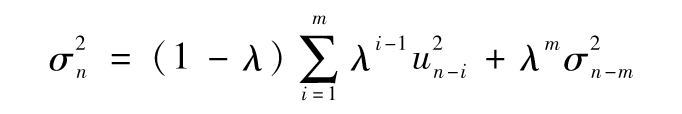
當m很大時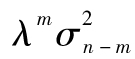，小到可以忽略，所以當α_i=（1-λ）λ^i-1時，式（10-8）與式（10-5）等價。對應於u的權重以λ速度遞減，每一項的權重是前一項權重與λ的乘積。

【例10-7】　假如λ為0.90，對應於第n-1天由市場變量所估測的波動率為每天1%。在第n-1天，市場變量增加了2%，這意味著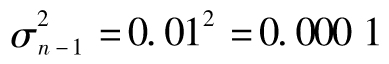以及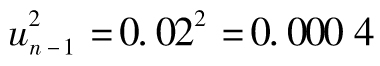，由式（10-8），我們得出

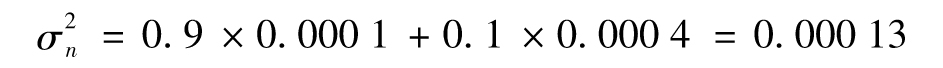
因此，第n天波動率σ_n的估計為，即每天1.14%。注意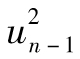的期望值為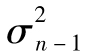，也就是0.000 1，這一例子中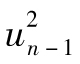，所對應的實際值比期望值要大，因此我們對於波動率的估計會增大。當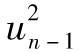的實際數值小於期望值時，我們對於波動率的估計值會減小。

EWMA方法的一個非常好的特性是該方法需要的數據相對較少。對於任一時刻，我們只需要記憶對當前方差的估計以及市場變量的最新觀察值。當我們得到市場變量的最新觀察值後，我們可以計算每天價格變化的比例，進而採用式（10-8）更新我們對方差的估計，這時更早的方差估計以及更早的市場變量數據可以被捨棄。

EWMA方法的出發點是對波動率進行跟蹤監測。假定市場在n-1天有一個較大的變化，那麼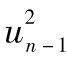也較大，由式（10-8）可以看出，這時對當前波動率的估計會增加。數值λ決定了當前估算出的日波動率估計對於最新市場變量日百分比變化的靈敏度。在計算σ_n時，對項，一個較低的λ會對應一個較大的權重。在這種情形下，對接下去幾天的波動率的估計本身就會有很大波動，而當λ較大時（接近於1），估算出的波動率對於新的日百分比變化率信息的反應會較為遲鈍。

由摩根大通建立並在1994年發佈的RiskMetrics數據庫中，採用λ=0.94來更新每天波動率估計。摩根大通發現對許多市場變量，這一選定的λ值生成的方差預測與實際方差非常接近。^[1]2006年以後，RiskMetrics更換了模型，轉而採用一個長記憶模型（long memory model）。相比EWMA模型，在新模型中隨i的增大，賦予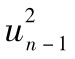項的權重衰減得要慢。

[1] See JPMorgan, RiskMetrics Monitor, Fourth Quarter, 1995.在這一章中我們採用另一種方法（最大似然估計）來估計參數，某一天實際的方差是對連續25天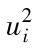的數據實施等權重平均計算得出的（見作業題10.20）。