e1 John Hull 風險管理與金融機構 v5
10.5 監測日波動率
定義σn為第n-1天結束時所估計的市場變量在第n天的波動率,相應的方差為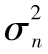 。假定市場變量在i天天末的價格為Si。定義ui為第i天連續複利收益率(第i-1天天末至第i天天末的收益),於是有
。假定市場變量在i天天末的價格為Si。定義ui為第i天連續複利收益率(第i-1天天末至第i天天末的收益),於是有
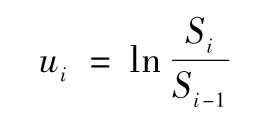
一種估計σn的方法是令其等於ui的標準差,利用ui最近m天的觀察數據和標準差的一般公式,我們得出

其中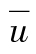 為ui的平均值
為ui的平均值
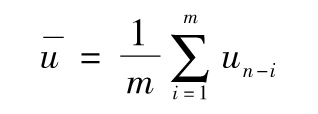
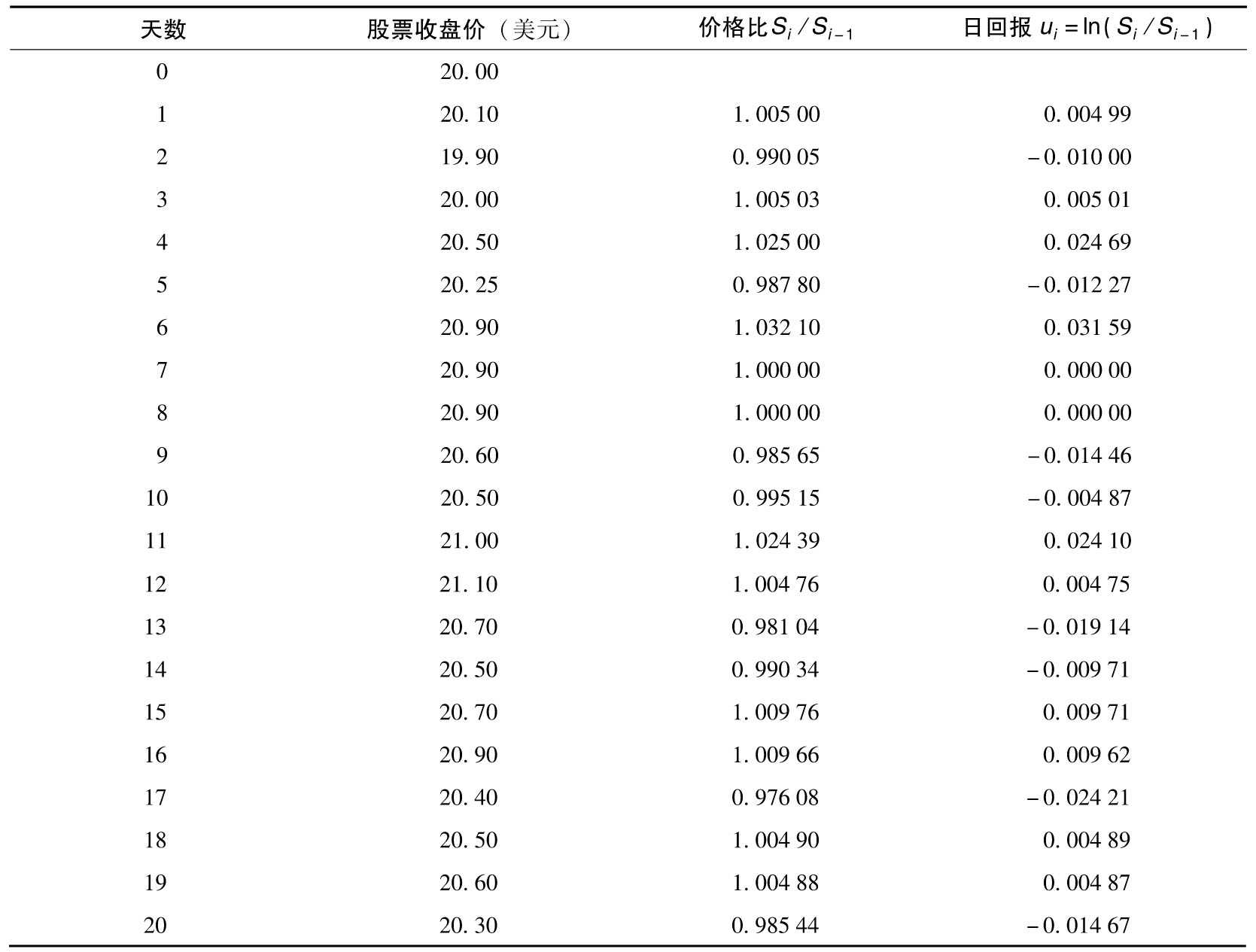
【例10-5】 表10-3顯示了股票價格的一個可能的序列。假設我們希望根據前20天對ui的觀察數據估計第21天的波動率,即n=21,m=20。在本例中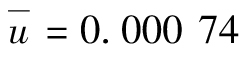 ,根據式(10-2)計算得出的日回報的標準差的估計值為1.49%。
,根據式(10-2)計算得出的日回報的標準差的估計值為1.49%。
表10-3 用來計算波動率的數據
式(10-2)的以下幾種變形常常被用於風險管理過程之中。
(1)如第10.1節中介紹的,ui被定義為市場變量在第i-1天天末與第i天天末的價格百分比變化

這種計算方式與前面計算ui的方式差別不大。
(2)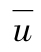 被假設為0:這種假設的前提是因為每一天市場變化期望值遠遠小於市場變化的標準差。[1]
被假設為0:這種假設的前提是因為每一天市場變化期望值遠遠小於市場變化的標準差。[1]
(3)m-1被m代替:這種做法將我們的波動率從無偏差估計轉換為最大似然估計(見第10.9節)。
以上三個變形會使得方差公式簡化為

其中ui由式(10-3)給出。
【例10-6】 再次考慮例10-5,當n=21,m=20時
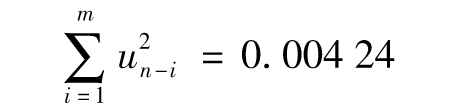
於是由式(10-4)
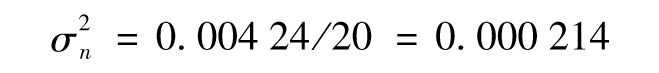
σn=0.014 618或1.46%。與例10-5相比變化很小。
加權方法
式(10-4)為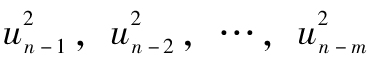 所有項賦予了相等的權重。我們的目標是估計第n天的波動率σn水平,因此賦予較新的數據更高的權重就具有合理性。一種這樣做的模型為
所有項賦予了相等的權重。我們的目標是估計第n天的波動率σn水平,因此賦予較新的數據更高的權重就具有合理性。一種這樣做的模型為

變量αi為i天前的觀察值所對應的權重,所有的α均為正。如果我們在對α賦值時保證在i>j時αi<αj,數據越久,所獲得的權重就會越低。所有權重之和必須為1,即
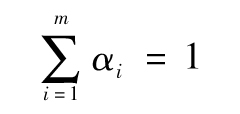
對於式(10-5)的理念,我們還可以做進一步擴展。假設存在某一長期平均方差,我們在考慮分配權重時,也應該將此均值考慮在內。這種擴展對應於以下模型

其中VL為長期方差,γ為VL所對應的權重,權重之和仍為1,我們有
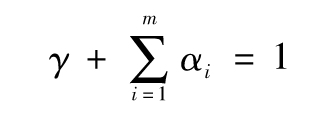
此模型被稱為ARCH(m)模型。這一模型最先由恩格爾(Engle)提出。[2]在這一模型中,方差的估計值與長期平均方差以及m個觀察值有關,觀察數據越陳舊,所對應的權重越小。令ω=γVL,我們可以將式(10-6)寫為

在接下來的兩節中,我們將討論兩種測算波動率的重要方法,這兩種方法均採用了式(10-5)及式(10-6)中的理念。
[1] 即使在我們所觀察的m天中,變量值增大或減小的速度非常快,這一假設也基本上是成立的。
[2] See R. F. Engle, “Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of U. K. Inflation,” Econometrica 50(1982):987-1008.羅伯特·恩格爾因對ARCH模型的貢獻而獲得2003年諾貝爾經濟學獎。