e1 John Hull 風險管理與金融機構 v5
10.4 冪律
冪律(power law)提供了正態分佈假設外的另一種方法。冪律指出,實踐中的許多變量的值,例如v,當x很大時,以下的關係式近似成立
Prob(v>x)=Kx-α
(10-1)
其中K及α為常數。上式已經被證明在許多情形下近似成立,這裡的變量可能是指個人的收入、城市的大小或者網頁每日被點擊的次數等。
【例10-4】 假定基於經驗,我們知道某個特定的金融變量α=3,並且觀察到v>10的概率為0.05,由式(10-1)得出
0.05=K×10-3
因此K=50。我們可以估計v>20的概率為
50×20-3=0.006 25
v>30的概率為
50×30-3=0.001 9
等等。
由式(10-1),我們可以得出
ln[Prob(v>x)]=lnK-αlnx
我們因此可以畫出ln[Prob(v>x)]與lnx的關係曲線來快速檢驗等式的正確性。為了將這一過程應用於表10-1中的數據,我們將v定義為匯率在一天內變化的標準差數量。
lnx和ln[Prob(v>x)]的價值在表10-2中進行了計算,圖10-3顯示了表10-2的數據。當x≥2時,匯率變化大於x個標準差的概率的對數近似和lnx呈線性關係,這說明了冪律的正確性。當x=3,4,5,6時,利用迴歸得出最佳匹配曲線為
ln[Prob(v>x)]=-0.735-3.291ln(x)
表10-2 由表10-1所得出的數值
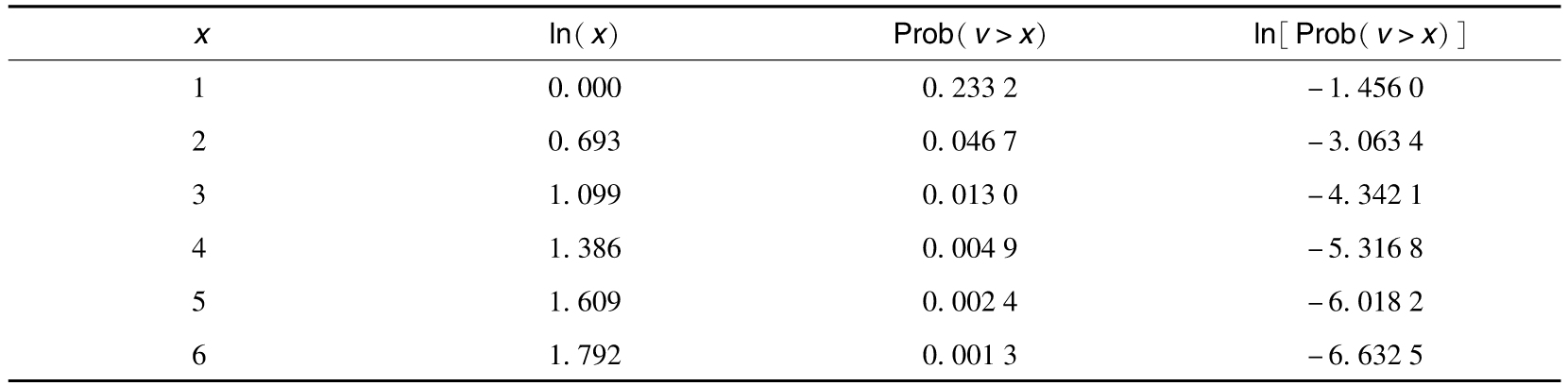
參數K和參數α的估計為:K=e-0.735=0.479,以及α=3.291。一個大於4.5倍標準差的增量的概率為
0.479×4.5-3.291=0.003 40
變化大於7倍標準差的概率為
0.479×7-3.291=0.000 794
在第13章討論極值理論時,我們將會較為正規地討論冪律以及給出更好的參數估計方式。在第23章中,我們將討論如何將冪律用於對操作風險進行檢測。
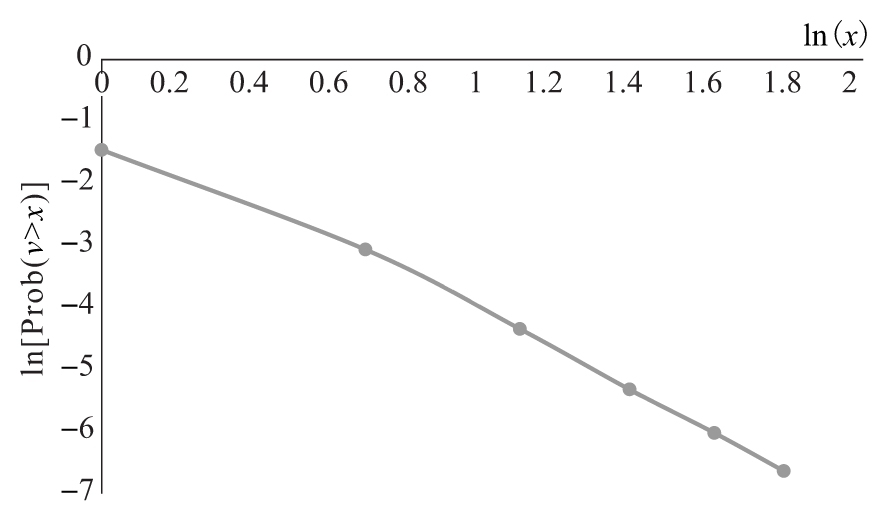
圖10-3 匯率變化超過若干標準差的概率的log-log圖
注:其中v是以標準差為度量的匯率變化量。