e1 John Hull 風險管理與金融機構 v5
10.1 波動率的定義
某個變量的波動率σ定義為這一變量在單位時間內連續複利回報率的標準差（見附錄A關於複利的討論）。當波動率被用於期權定價時，時間單位通常定義為1年，因此波動率就是1年的連續複利回報率的標準差。但當波動率被用於風險控制時，時間單位通常是1天，此時的波動率對應於連續複利的日回報率的標準差。
定義Si為一個變量在日期i結束時的值，則該變量連續複利的日回報為
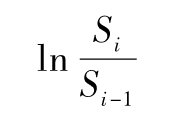
這與下式基本相等
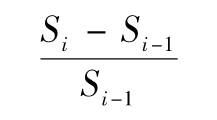
因此，日波動率的另外一種定義是變量的日相對變化的標準差。這個定義也是風險管理中常用的定義。
【例10-1】 假定一個資產的價格是60美元，日波動率為2%。這意味著一天中資產價格出現一個標準差的變化等於60×0.02，即1.20美元。如果我們假設資產價格變化服從正態分佈，則我們有95%的把握確信，在一天結束時，資產的價格將在60-1.96×1.2=57.65美元和60+1.96×1.2=62.35美元之間（這就是雙尾檢驗，即各有2.5％的概率落在分佈的上尾和下尾）。
如果我們假設，每日的回報是相互獨立的且具有同樣的方差，則T天的回報的方差為T乘以每日回報方差的積。這意味著，T天回報的標準差是日回報標準差的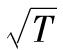
倍。這和“不確定性隨時間長度的平方根增長”這一法則是一致的。
【例10-2】 假設例10-1中資產的價格是60美元，日波動率為2%，則5天連續複利的回報率的標準差是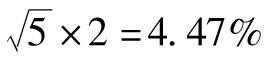
。因為5天是一個較短的時間，所以我們可以認為這和5天來價格相對變化的標準差相等。一個標準差的移動對應的價格變化為60×0.044 7=2.68美元。如果我們假設，資產價格的變化服從正態分佈，則我們有95%的把握確信，在第5天結束時，資產的價格位於60-1.96×2.62=54.74美元和60+1.96×2.68=65.26美元之間。
10.1.1 方差
風險管理人員常常關心方差而不是波動率。方差被定義為波動率的平方。年方差對應於變量在1年內連續複利變化的方差。在時間T內變化的標準差與時間的平方根成正比，而方差與時間成正比。嚴格來講，我們應該說方差對應於每天的變化，而波動率對應於每天的平方根的變化。
10.1.2 交易天數與日曆天數
在計算波動率時，會產生以下的問題：我們應該採用日曆天數還是交易天數？如業界事例10-1所示，研究人員已經證明在交易所營業日的波動率比在交易所非營業日的波動率要大很多，因此當由歷史數據估計波動率時，分析員常常忽略週末和節假日，在計算時通常的假定是每年有252個交易日。
業界事例10-1
什麼因素觸發了波動率
有一種關於波動率的自然假設，那就是波動率是由剛剛到達市場的新信息引起的。這些消息促使投資者改變對股票價格的觀點。股票價格變化也促成了波動率的變化，但是這種有關波動率變化根源的觀點沒有得到研究結果的支持。
應用連續幾年的每日資產價格數據，研究人員可以計算：
（1）在中間不包含非交易日時，一個交易日結束時與下一個交易日結束時資產價格回報率的方差；
（2）在週五結束時與下週一結束時資產價格回報率的方差。
第2項為3天收益率的方差。第1項對應於1天的方差。我們也許很自然地認為第2項方差為第1項方差的3倍。法瑪（Fama，1965）、弗倫奇（French，1980）以及弗倫奇和羅爾（French and Roll，1986）證明事實並非如此。三項研究結果分別證明第2項方差只分別比第1項方差高22%、19%以及10.7%。
這時，你也許會說這些結果是由於在交易開盤時有更多信息，但是羅爾（1984）的研究結果並不支持這一觀點，羅爾檢測了橙子的期貨價格。對於橙子的期貨價格而言，最重要的決定因素是氣候，而有關氣候的信息對於任何時間都有同樣的到達頻率，當羅爾做了一個類似我們剛剛描述的有關股票的分析時，他發現第2項（週五至週一）方差只是第1項的1.54倍。
唯一合理的結論就是波動率在某種程度上是由交易本身造成的（當然對這一結論，交易員接受起來沒有任何困難）。
設σyr為某一資產的年波動率，σday為相應的每天波動率。假設連續交易日的回報是獨立的，並有相同的標準差，這意味
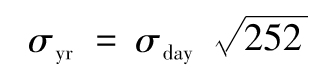
或
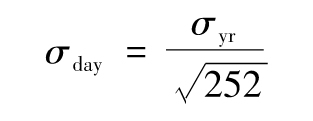
以上關係式說明，日波動率大約為年波動率的6%。