e1 John Hull 風險管理與金融機構 v5
9.7 主成分分析法
對於任意一個零息收益曲線,前面所述方法可能會要求分析員計算10~15個不同的delta。這看起來似乎有點小題大做,因為曲線上的變量相互之間是高度相關的。例如,曲線上5年期的收益率變化了若干基點,在大多數情況下,10年期的收益率變化也大致如此。當一個交易員在5年期有一個很大的正風險敞口,而對應於10年期有一個類似的負風險敞口時,此時該交易員不應該太擔心利率的變化。
一種可用來分析高度相關的市場變量的風險的方法是主成分分析法(principal component analysis),這種方法以市場變量的歷史變化數據為依據,並試圖從中找出解釋這些變化的主要成分或因素。
通過一個實例,我們可以更好地解釋這一方法。我們考慮的市場變量是期限為1年、2年、3年、4年、5年、7年、10年和30年的8個不同的互換利率,表9-6及表9-7顯示了基於2000~2011年2780個交易日的觀察數據產生的結果。表9-6中第1列顯示了利率期限,表中其他列顯示出描述利率變化的8個因子(主要成分)。第1個因子對應於利率曲線變化的平行移動,這一因子是表中的PC1。一個單位的PC1對應的1年期利率增加量為0.216基點,2年期利率的增加量為0.331個基點,依此類推;第2個因子位於PC2列,這一因子對應於收益率曲線的扭動(twist)或曲線坡度的變化,1~4年期利率變化為同一方向,5~30年期利率變化為另一方向;第3個因子PC3對應於利率曲線弓伸(bowing)現象,對應於這一因子,短期(1~2年)及長期利率(10~30年)朝同一方向移動,而中期利率會朝另一相反方向移動。因子所對應的利率變動被稱為因子載荷(factor loading)。在我們的例子中,對於1年期利率,第1個因子的因子載荷為0.216。[1]
表9-6 互換利率的因子載荷

表9-7 因子得分的標準差

我們的分析涉及8個利率變量以及8個因子,通過對一線性8元方程求解,可以將任意一天的利率變化表達為變化因子的線性組合,任意一天的利率變化對應某一因子的係數也被稱為這一天利率變化的因子得分(factor score)。
因子的重要性是通過因子得分的標準差來反映的,我們將例子中因子得分的標準差列在表9-7中,並按重要程度進行排列。在分析中,利率變動的計量單位為基點。因子的單位是標準差。因此第一個因子對應的1年期利率變動為0.216×17.55=3.78個基點,2年期利率變動為0.331×17.55=5.81個基點,依此類推。
用來計算表9-6和表9-7中結果的軟件可以在作者的網頁上找到。計算過程在附錄I中做了說明。主成分分析法是一個標準的統計工具。要進行主成分分析,第一步需從觀測中計算出一個方差-協方差矩陣(見第14章關於方差-協方差矩陣的討論)。在我們的例子中,該方差-協方差矩陣有8行8列,其中第1行第1列對應的是1年期利率日變動量的方差,第1行第2列對應的是1年期利率和2年期利率日變動量的協方差,依此類推。因子載荷是由該矩陣算出的特徵向量,而因子得分是由該矩陣算出的特徵值(對特徵值和特徵向量的解釋見附錄H)。
因子具有的一個性質是因子得分沒有相關性。在我們的例子中,第1個因子得分(平行移動數量)與第2個因子得分(扭動數量)在2 780個觀察日內相互獨立。因子得分的方差滿足以下性質:其和等於整個數據的方差。由表9-7得出,數據的整體方差(也就是1年期利率的觀察值的方差,2年期利率的觀察值方差等)為
17.552+4.772+2.082+…+0.532=338.8
由此可以看到第1個因子解釋了17.552/338.8=90.9%的原始數據的變化;前兩個因子解釋了(17.552+4.772)/338.8=97.7%的數據變化;第3個因子又進一步解釋了1.3%的數據變化。這說明,大部分利率變化中的風險可以由前兩個或前三個因子來解釋,這意味著我們可以將利率產品組合的風險同這些主要因子聯繫起來,因此我們並不需要考慮所有8個不同的利率。我們在圖9-8中畫出了表9-6所示的三個最重要的因子。[2]
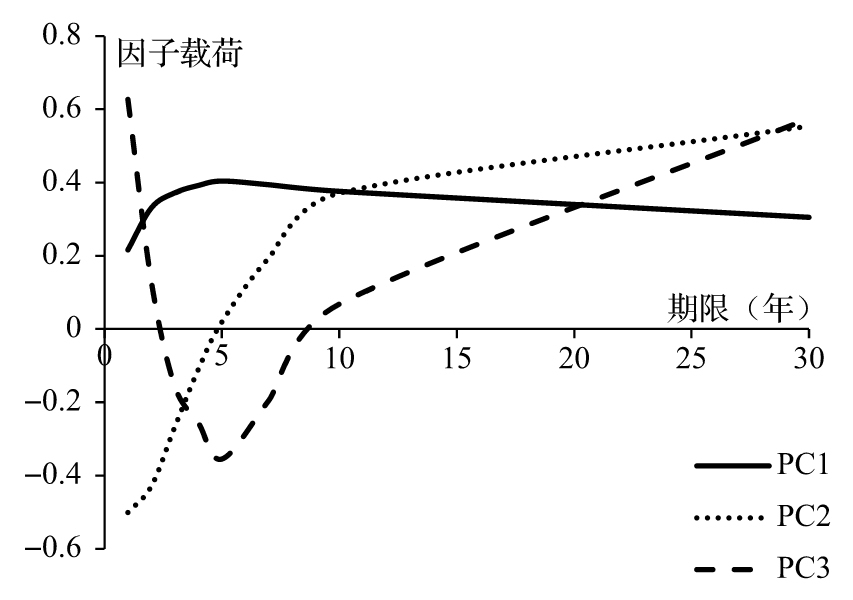
圖9-8 驅動利率變化的三個最重要因素
應用主成分分析法來計算delta
主成分分析法給計算delta提供了又一種有效的途徑。為了說明這一點,假定我們擁有一個交易組合,其對於利率變化的敞口如表9-8所示。3年期利率變化一個基點觸發組合價值增加量為1000萬美元;4年期利率變化一個基點觸發組合價值增加量為400萬美元等。如果我們採用前兩個最重要因子來模擬利率變化(如前所述,這兩個因子解釋了97%的利率變化),應用表9-6中的數據,我們算出第1個因子的delta敞口(對於每一個因子得分的一個基點變動所觸發的以百萬美元為單位的變動數量)為
10×0.372+4×0.392-8×0.404-7×0.394+2×0.376=+0.05
及第2個因子的delta敞口為
10×(-0.267)+4×(-0.110)-8×0.019-7×0.194+2×0.371=-3.88
表9-8 與一個基點利率變化相對應的交易組合價值變化 (百萬美元)

這裡的計算方法與第9.6節所描述的用局部久期來解釋非平行移動的方法相似。應用主成分分析法的優點是,這種方法會告訴你利率的哪種不同變化形式更為重要。在剛才的例子中,我們看到交易組合對於第2種利率變化的敞口是對於第一種變化敞口的80倍;但是,基於表9-7,第1種變化的標準差是第2種變化的標準差的3.7倍。某因子對於一個特定的交易組合的重要性可以通過delta敞口與因子得分的標準差的乘積來衡量。採用這個方法,對錶9-8中的交易組合,第2個因子的重要性是第1個因子的20倍。
[1] 因子載荷有一個性質:所有載荷因子的平方之和為1.0。另外,要注意,如果所有因子載荷的符號發生變化,因子不變。
[2] 將主成分分析法應用於任何一個國家的任意一收益曲線所得出的主要因子含義及解釋整體風險的數量與這裡陳述的結論基本相同。