e1 John Hull 風險管理與金融機構 v5
9.6 收益曲線的非平行移動
不幸的是,利率久期的關係式(9-6)只適用於利率曲線的平行移動,由久期和凸性所組成的關係式(9-7)雖適用於較大規模的利率變動,但變動形式仍應是平行移動。
9.6.1 局部久期
一些研究人員已經擴展了久期方法以使其適用於收益曲線的非平行移動。Reitano(1992)提出了一種局部久期度量方法。在這一方法中零息收益曲線只在局部一點變動,而收益曲線的其他點保持不變。[1]例如,假定零息收益率由表9-4及圖9-4所示,將收益曲線上第5年所對應的點按圖9-5所示的形式進行移動。假定零息曲線上有n個點,交易組合對於收益曲線上第i點的局部久期Di的定義為
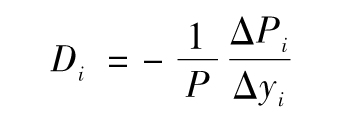
其中P為交易組合的價值,Δyi對應於收益曲線上第i個點的變動幅度,ΔPi是所對應交易組合的價值變化量。所有局部久期的和等於通常意義下的整個久期。[2]由於零息曲線第i個節點的變化Δyi所觸發的組合價值的相對變化為-DiΔyi。
表9-4 某零息收益率曲線(利率為連續複利)

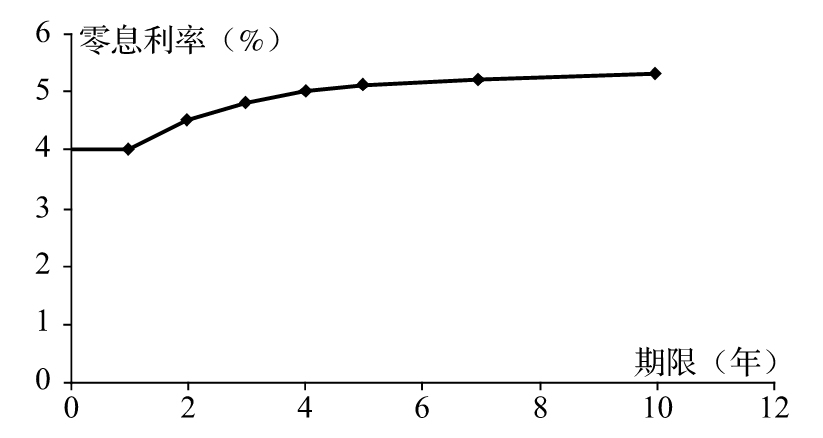
圖9-4 與表9-4對應的零息利率曲線
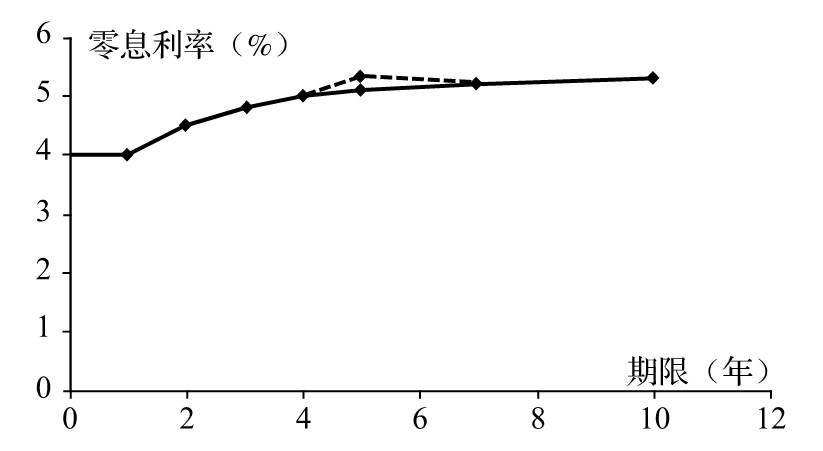
圖9-5 當某一點移動時零息收益率曲線的變化
假定表9-5顯示的是某交易組合的局部久期。整個交易組合的久期(各局部久期之和)僅僅為0.2,這說明交易組合對於收益曲線的平行移動並不是很敏感。但是從表中我們可以看到,對應於短期期限的久期為正,對應於長期期限的久期為負,這說明當短期利率上升(下降)時組合會有損失(收益),當長期利率上升(下降)時組合會有收益(損失)。
表9-5 某一投資組合的局部久期

我們現在可以進一步說明非平行移動對交易組合的影響,進一步計算投資組合價值對任何非平行移動變動的敏感性,定義一種旋轉方法,對應於1年、2年、3年、4年、5年、7年及10年的利率變動量為-3e、-2e、-e、0、e、3e及6e,這裡e為一個很小的值。圖9-6是此旋轉的圖形顯示。採用表9-5中的局部久期數據,我們得出由於收益曲線旋轉導致的交易組合價值的相對變化為
-[0.2×(-3e)+0.6×(-2e)+0.9×(-e)+1.6×0+2.0×e-2.1×3e-3.0×6e]=25.0e
對於曲線的一個小的平行移動e,交易組合價值的相對變化為-0.2e。這一結果顯示具有表9-5所示的局部久期的交易組合對於曲線旋轉的敏感性遠大於對平行移動的敏感性。
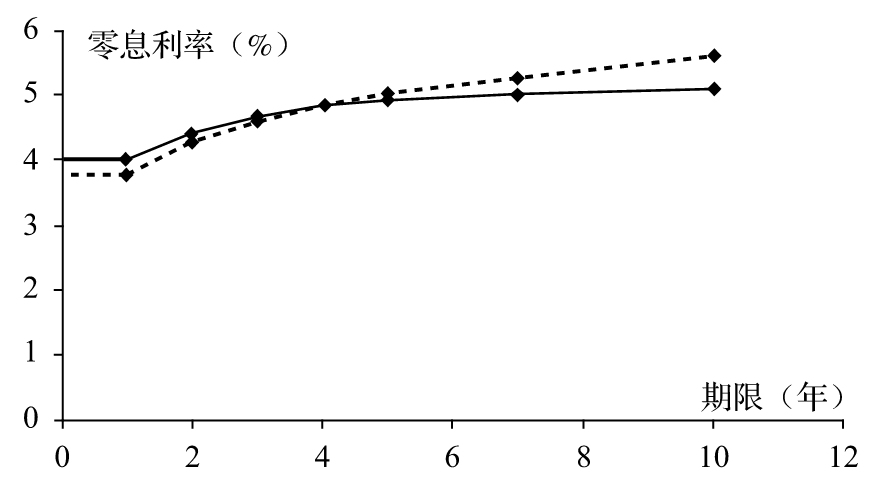
圖9-6 利率曲線的旋轉
在第9.5節中,我們解釋了通過將投資組合的價值乘以投資組合的久期,可以測度絕對額久期。類似地,局部久期是投資組合的變化率相對於期限結構一個頂點的微小變化的delta。
9.6.2 分段delta
局部久期的一種變形方法是,首先將收益曲線分成幾段或幾個區間(bucket),然後計算每一部分的變動對於交易組合的影響,在改變任意部分的利率時,要保證其他部分的利率不變。這種方法常常被應用於資產負債管理過程(見第9.1節),該管理方法也被稱為缺口管理(GAP management)。圖9-7將圖9-4所示的曲線中介於2年至3年的部分進行移動,類似於局部久期方法,所有部分的delta之和也等於DV01。
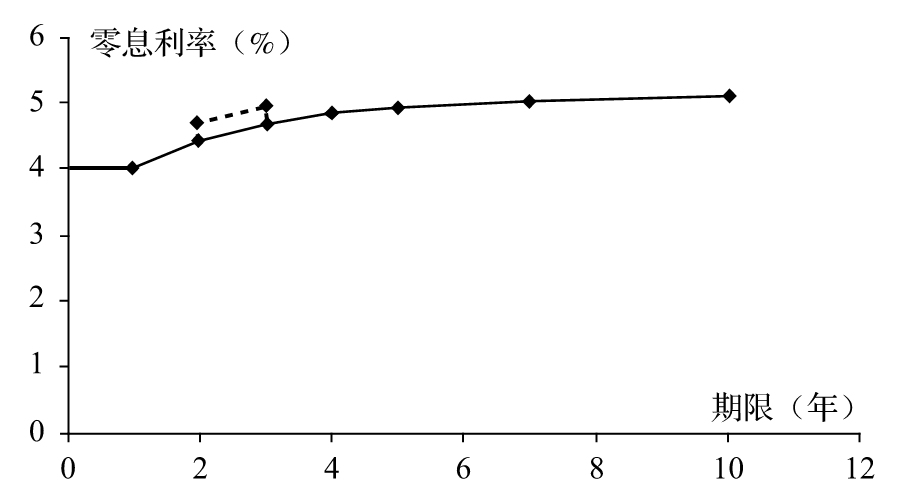
圖9-7 某區間的利率曲線變化
9.6.3 計算delta用於對衝
截至目前,我們考慮的敞口度量並不是為了方便對衝而設計的。考慮如表9-5所示的局部久期,假定我們打算用零息債券來對衝我們的交易組合,我們可以計算出1年期零息債券的頭寸來對衝2年期的利率變化。同樣我們也可以計算出2年期零息債券的頭寸來對衝2年期的利率變化,並依此類推。但是如果在對衝中採用其他工具,則對衝難度會大大增加。
在實踐中,交易員往往採用那些用於生成零息收益率曲線的產品來對衝他們的風險敞口。例如,在對衝時,一個政府債券交易員喜歡採用在市場上最活躍的,並被用來構造零息收益率曲線的政府債券。又如,當交易產品和LIBOR/互換曲線有關時,交易員更可能採用LIBOR存款、歐洲美元期貨以及互換交易等來對衝。
為了便於對衝分析,交易員常常測算那些用於構造零息收益率曲線的產品價格的微小變動對於交易組合的影響。當價格有微小變化時,零息收益率曲線會被重新產生,組合也會被重新定價。考慮某個負責交易利率上限期權(caps)以及利率互換期權(swap options)的交易員,假定對應於某一歐洲美元期貨報價的每一個基點變動,交易員的交易組合價格變化為500美元,而對應於一個基點價格變動,期貨價格變化為25美元,因此交易員可以採用20個期貨來對衝其風險;假定對應於5年期互換利率的一個基點變化,交易組合價格變化為4 000美元,而對應於這一5年期互換利率變化,一個5年期面值100萬美元的互換價格變化為400美元,因此交易員可採用一個面值1 000萬美元的互換來對衝其交易組合。
[1] See R. Reitano, “Nonparallel Yield Curve Shifts and Immunization,” Journal of Portfolio Management (Spring 1992):36-43.
[2] 當零息曲線的第i個點被移動而其他點不動時,這時的零息曲線是由被移動點和不被移動點的插值來生成的,如圖9-5所示。