e1 John Hull 風險管理與金融機構 v5
9.5 推廣
到目前為止,我們採用了久期和凸性來檢測單一債券對利率的敏感度。久期和凸性可以被推廣到債券組合,或其他與利率相關的產品組合。我們將零息收益曲線的平行移動定義為將零息收益曲線上的所有點平行移動一個相同的數量(見圖9-3)。
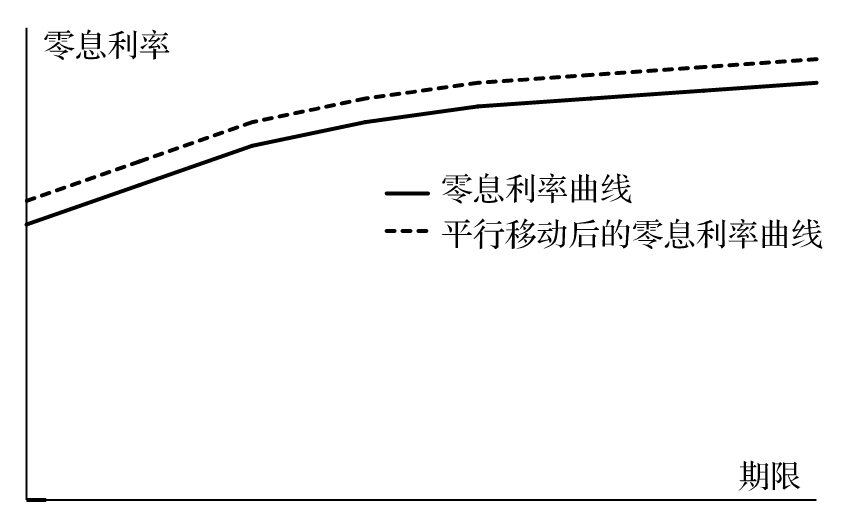
圖9-3 零息利率的平行移動
假定P代表組合的價值,將零息收益曲線進行一平行移動,我們觀察到相應價格的變化為ΔP,久期被定義為
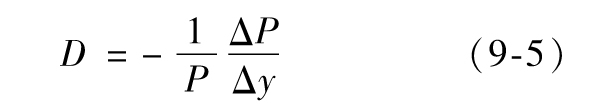
其中Δy為平行移動的變化量,[1]式(9-5)等價為

假定組合由多種跟利率相關的資產組成,第i個資產價值為Xi,其對應的久期為Di(i=1,2,…,n)。定義ΔXi為收益率變化Δy時的Xi的相應變化量,定義 ,根據式(9-5),整個組合的久期為
,根據式(9-5),整個組合的久期為
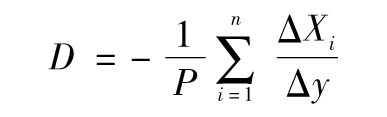
關於第i項資產的久期,由以下公式給出

因此
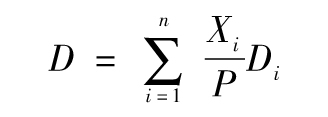
這一公式說明投資組合的久期D是其構成資產久期的加權平均,權重等於構成資產與整體組合價值的比率。
交易組合的絕對額久期D$可被定義為交易組合的久期乘以組合的價值,即
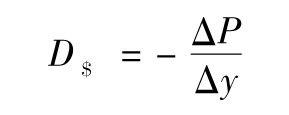
絕對額久期是交易組合對於利率的delta,與利率有關的產品所組成的交易組合的絕對額久期等於交易組合的構成資產的絕對額久期的總和。
凸性的概念同樣也可以像久期那樣推廣。假定一個與利率相關的組合其價格為P,我們定義組合的凸性C為1/P乘以組合的價值對零息收益曲線平行移動二階偏導的乘積,將B替換為P,式(9-4)仍然正確

這個公式說明了組合的凸性與構成組合的資產的凸性關係。這一關係與久期的關係式相似,也就是說,組合的凸性等於構成資產的凸性的加權平均,其權重為構成資產價格佔整體組合價格的比率。當一個交易組合的久期為一個特定值時,如果現金流在一個較長的時間內有較為均勻的分佈,則交易組合的凸性會趨向最大,而當現金流侷限在一個時間點時,債券組合的凸性趨向最小。
價值為P的交易組合的絕對額凸性可被定義為P乘以組合的凸性。絕對額凸性給出了交易組合對利率的gamma。與利率有關的產品所組成的交易組合的絕對額凸性等於組合的構成資產的絕對額凸性的總和。
交易組合免疫
通過保證久期為0,我們可以使得一個與利率有關的交易組合(由空頭和多頭組成)價值不受收益曲線小規模平行移動的影響。保證久期及凸性均為0或者接近於0,我們可以使得交易組合價值不受收益曲線較大規模的平行移動的影響。
[1] 零息收益曲線平行移動Δy數量所引起的債券收益率的變動大約為Δy。