e1 John Hull 風險管理與金融機構 v5
9.4 凸性
對於收益曲線一個較小的平行移動,久期可以度量組合價值的相應變化。圖9-2表明具有相同久期的兩個債券,它們的相對價格變化和收益率變化之間的關係可以不同。這兩個債券在起始點的導數(切線)相同。這意味著,當收益率有較小的變化時,兩個債券價值變化同收益率變化的百分比相同,這與式(9-1)一致。當利率變化較大時,兩個債券的表現就不一樣了。債券X的曲率比債券Y要大。一個被稱為凸性(convexity)的變量是用來度量曲線的凸凹變化的程度,它可被用來改善近似式的準確性。
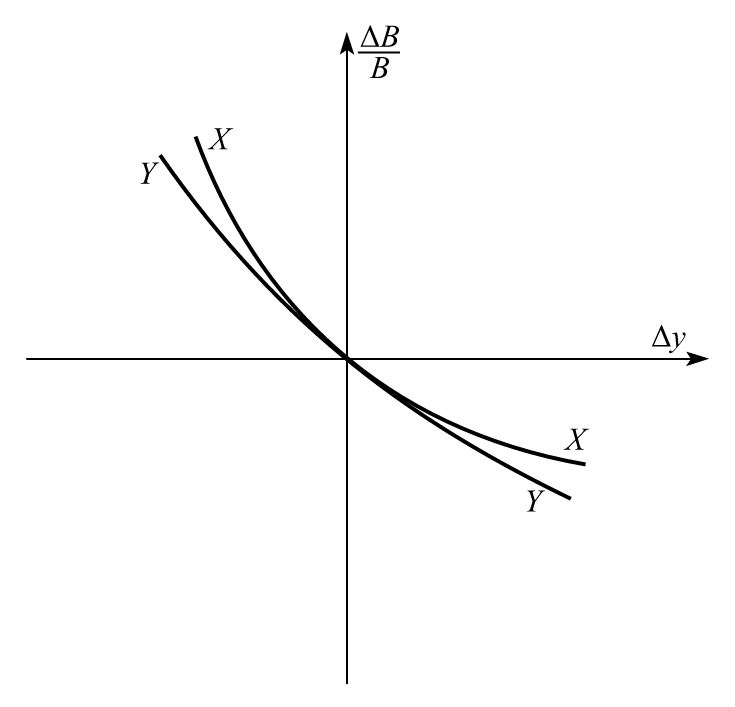
圖9-2 兩個久期相同、凸性不同的債券
債券凸性的定義為
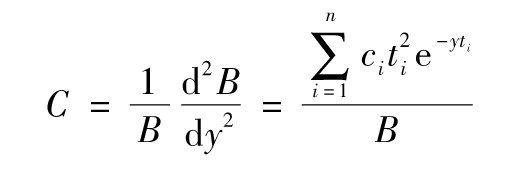
其中y對應於債券的收益率,以連續複利表示。債券凸性是將來收到現金流的時間平方的平均值,由附錄G的結論,我們可以得出關於債券價格的兩階近似式
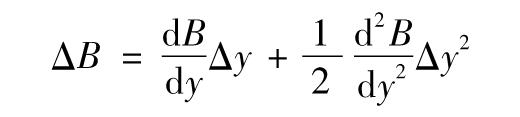
由此
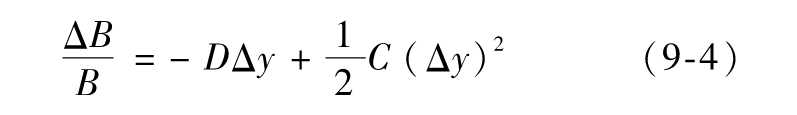
【例9-3】 由表9-3描述的債券B的價格為94.213,久期為2.653,凸性為
0.05×0.52+0.047×1.02+0.044×1.52+0.042×2.02+0.039×2.52+0.779×3.02=7.570
由式(9-4)得出
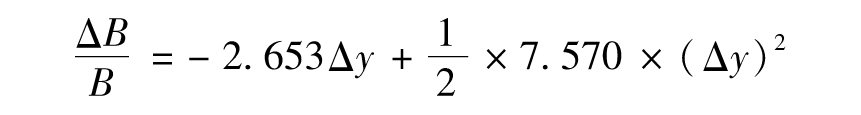
假設債券收益率由12%變為14%,即變化量為2%,久期公式預計債券價值變化將是-94.213×2.653×0.02=-4.999,凸性關係式預計變化為
-94.213×2.653×0.02+0.5×94.213×7.750×0.022=-4.856
而證券價格的實際變化為-4.859。這個例子說明:當債券收益率變化較大時,凸性公式比久期公式更為精確。
絕對額凸性
絕對額凸性(dollar convexity)C$的定義與絕對額久期類似,它等於凸性與債券價格的乘積,這意味著
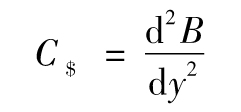
絕對額凸性類似於我們在第8章中討論的gamma測度。