e1 John Hull 風險管理與金融機構 v5
8.7 泰勒級數展開
在附錄G中,我們解釋了泰勒級數(Taylor series)展開過程,泰勒級數展示了在某一短時間內各個希臘值在交易組合變化中所起的不同作用。假設某交易組合價值只與某單一標的資產(變量)有關,並且利率及標的資產的價格波動率為常數。作為標的資產(變量)價格S以及時間t函數,交易組合價格P的泰勒展開式為
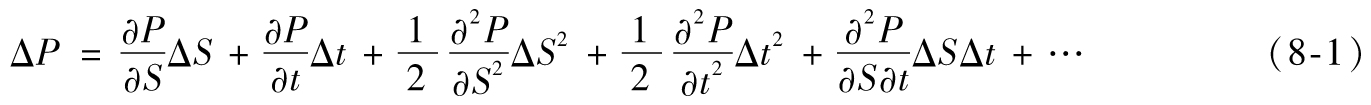
其中ΔP及ΔS分別對應於在某一短時間Δt內P以及S的變化。delta對衝可將上式右端第1項消除,第2項對應於時間損耗,是一個非隨機項,第3項可以在保證gamma中性時被消除,隨機微分方程理論顯示出ΔS的誤差級別與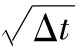 相同,這意味著右端第3項的誤差級別為Δt,右端的其他項的誤差級別高於Δt。
相同,這意味著右端第3項的誤差級別為Δt,右端的其他項的誤差級別高於Δt。
對於一個delta中性的交易組合,式(8-1)的右端第1項為0,因此

在以上表達式中,我們忽略誤差級別高於Δt的項。圖8-9顯示了交易組合價值的變化同標的資產價格的變化的曲線。當gamma為正時,如果標的資產價格的變化幅度較大,那麼交易組合會有正收益;當標的資產價格的變化幅度較小或不變時,交易組合收益會為負。當gamma為負時,以上結論相反,即標的資產價格的一個較大變動會給交易組合帶來嚴重的損失。
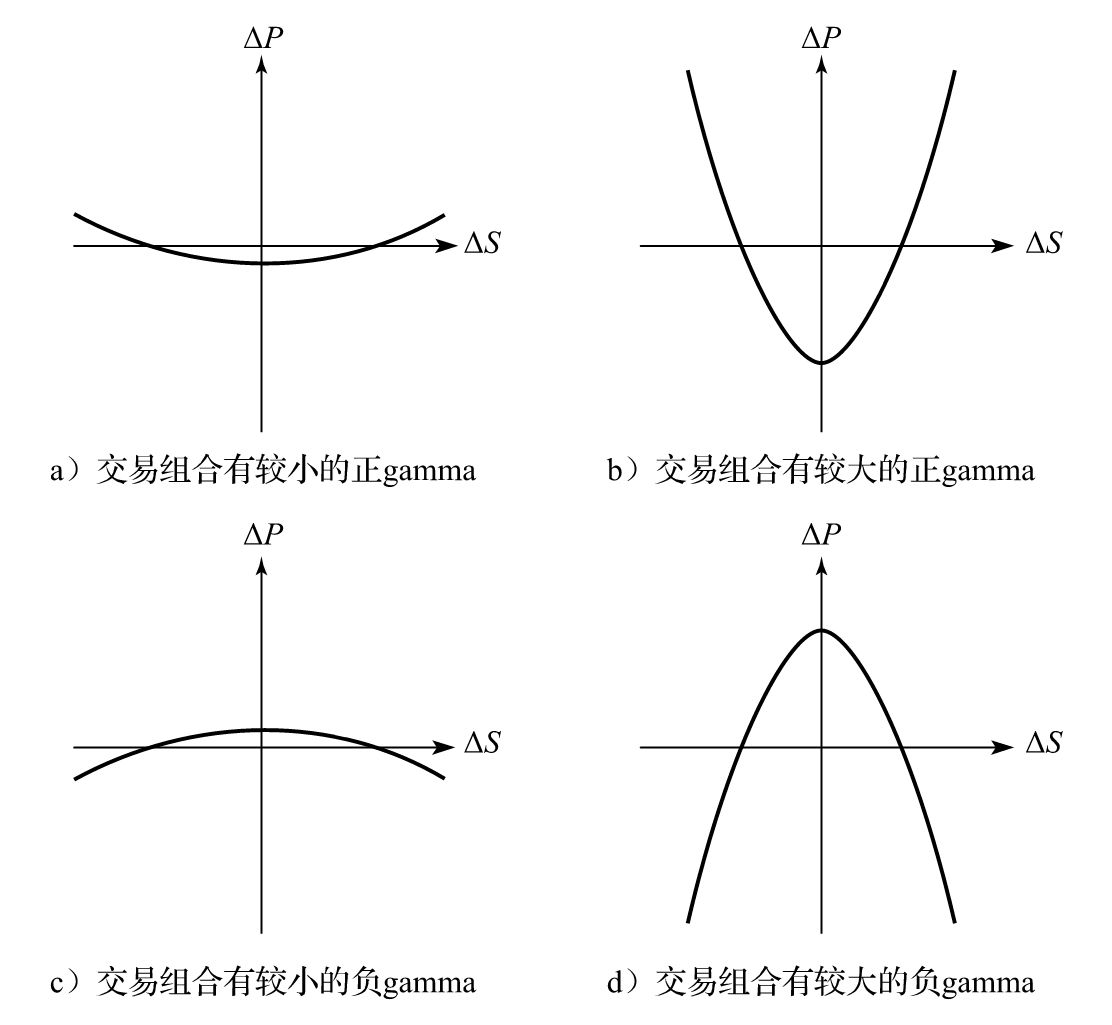
圖8-9 delta中性的交易組合的ΔP與ΔS之間的幾種關係
當標的資產價格波動率也為變量時,作為σ、S以及t的函數,交易組合價格的泰勒方程展開式為
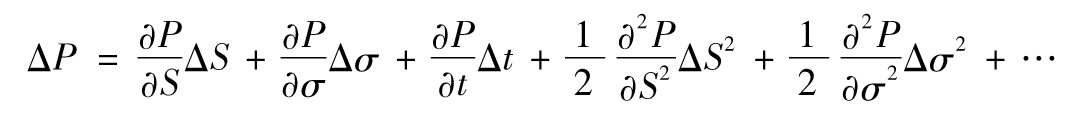
其中Δσ為波動率在Δt內的變化量。此時,delta中性可以消除右端第1項。vega中性可消除第2項,第3項為非隨機項,第4項可被gamma中性消除。
交易員經常也會對泰勒展開式的高次項進行定義,例如,∂2P/∂S∂σ被稱為vanna,∂2P/∂σ2被稱為vomma,∂2P/∂S∂t被稱為charm。
【例8-2】 假定一個delta中性的交易組合的gamma為-10 000,並且在某個短的時間段,資產價格變化為+2(Δt可以假設為0)。式(8-2)顯示,交易組合非預期減值大約為0.5×10 000×22=20 000美元,注意如果價格變化為-2,則非預期減值數量相等。