e1 John Hull 風險管理與金融機構 v5
8.3 vega
衍生產品交易的另一個風險來自標的資產價格波動率的變化。一個市場變量的波動率是用來衡量此變量將來價值的不確定性(這一概念會在第10章中被詳細討論)。在期權定價模型中,波動率經常被假設成常數,而在實踐中,波動率會隨時間而變化。現貨產品、遠期、期貨及互換產品的價值與標的資產的市場價格的波動率無關,但期權及大多數更復雜的衍生產品的價格與標的波動率有關,這些產品的價值會因為標的資產的價格、資產價格的波動率及時間的變化而變化。
一個交易組合的vega(V)是指交易組合價值變化與標的資產價格波動率變化的比率,其定義為[1]
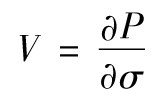
如果一個交易組合的vega絕對值很大,此交易組合的價值會對波動率變化非常敏感,當一個交易組合的vega絕對值較小時,資產波動率的變化對交易組合的價值影響也會很小。
在某個交易組合中加入某個在市場上交易的期權會改變交易組合的vega,假定某交易組合的vega為V,可交易期權的vega為VT,在交易組合中放入頭寸為-V/VT的可交易期權可使最初的交易組合vega呈中性。但不幸的是,一個gamma中性的交易組合一般不會是vega中性,投資者想使得一個交易組合同時達到gamma及vega中性,就必須引入與標的資產有關的兩種不同衍生產品。
【例8-1】 假如某一交易組合為delta中性,gamma為-5000,vega為-8000。設某個可交易期權的gamma為0.5,vega為2.0,delta為0.6。購買數量為4000的該交易期權會使得交易組合呈vega中性,這樣做同時會使得delta增至2400,因此為了保證delta中性必須賣出2400單位的標的資產,交易組合的gamma也會從-5000變成-3000。

為了保證交易組合gamma及vega中性,我們引入第二個可交易期權。此期權的gamma為0.8,vega為1.2,delta為0.5。我們用w1及w2來代表兩個可交易期權的頭寸,我們要求
-5000+0.5w1+0.8w2=0
-8000+2.0w1+1.2w2=0
以上兩個方程式的解為w1=400,w2=6000。因此加入400份上述第一種及6 000份上述第二種交易所交易期權會使得交易組合gamma及vega都呈中性。加入這兩種期權後,交易組合的delta變為400×0.6+6 000×0.5=3 240,因此必須賣出3 240份標的資產,以保持交易組合的delta中性。
期權的多頭寸方的vega為正。圖8-6顯示了vega隨標的資產價格變化的關係曲線圖。vega圖形同gamma圖形較為相似。gamma中性在兩次對衝平衡交易之間,標的資產價格發生較大幅度變化的情況下,為交易組合的價值提供保護;vega中性在兩次對衝平衡交易之間,標的資產價格波動率發生變化的情況下,對交易組合的價值提供保護。
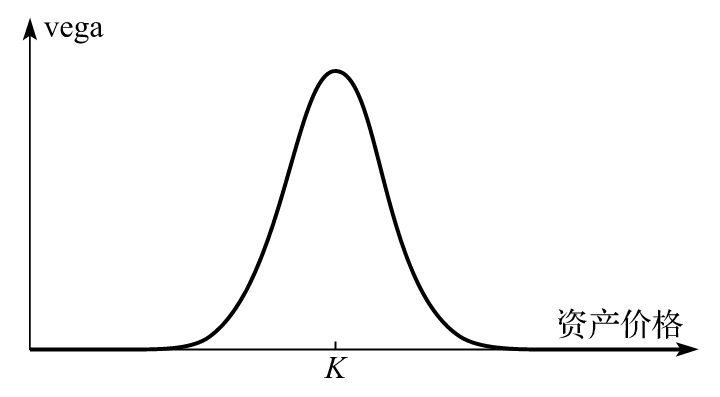
圖8-6 期權vega與標的資產價格的關係,K為期權執行價格
期限較短的期權的波動率比期限較長的期權波動率更具有多變性,因此在計算交易組合vega時,通常對期限較短的期權波動率的擾動量要比對期限較長的期權波動率的擾動量大,這一點將在第10.10節中討論。
[1] vega雖然是期權定價中“希臘值”的一個名稱,但是vega本身並不在希臘字母表中。