e1 John Hull 風險管理與金融機構 v5
8.1 delta
假如你是美國某家銀行的交易員,你負責銀行所有與黃金有關的交易。當前黃金價格為每盎司1 300美元。表8-1顯示了你所持有的交易組合(也被稱為交易賬本或賬戶,“book”),你應該如何管理你所面臨的風險呢?
表8-1 某一黃金交易組合
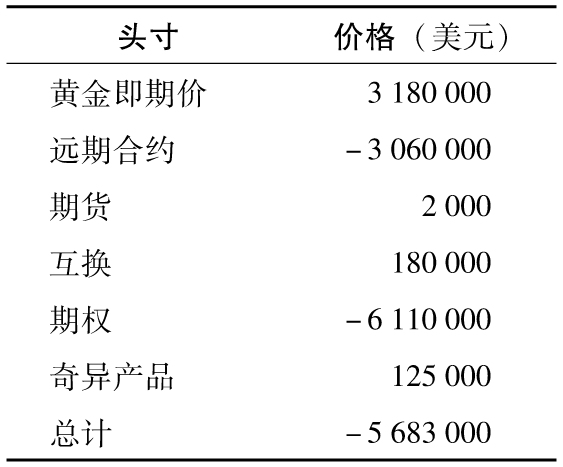
這裡你所持有的交易組合的當前價值為-5 683 000美元(這可能部分是因為你一直是期權的淨賣方,部分是因為市場走勢不利於你),一種檢測你的交易組合所面臨風險的辦法是假定黃金的價格由現在每盎司1 300美元變為每盎司1 300.10美元,然後再重新對你所持交易組合進行估價。假定當黃金價格變化後,交易組合的價格從-5 683 000變為-5 683 100美元。黃金價格增加0.1美元會觸發交易組合損失100美元,因而交易組合對黃金價格的敏感性為
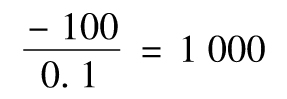
以上所討論的敏感性就是交易組合的delta。對應於每一美元黃金價格的上漲,交易組合損失1 000美元。類似地,我們可以計算出對應於每一美元黃金價格的下降,交易組合會有1 000美元的收益。
通常來講,交易組合價值對應於市場變量的delta由以下表達式來定義
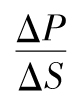
這裡的ΔS是指市場變量的微小變化,而ΔP對應於隨之而來的交易組合的價值變化。採用微積分的術語,delta(希臘字母中為Δ)是指交易組合價值對某一市場變量的偏導數,也就是說
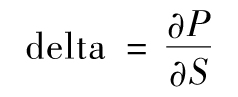
在我們的例子中,交易員可以買入1 000盎司黃金來消除delta風險。這是因為持有1 000盎司黃金的delta也是1000。當黃金價格每盎司增加1美元時,持有1 000盎司的黃金會產生1 000美元的收益,這被稱為delta對衝(delta hedging)。買入的黃金與最初交易組合迭加所產生的新的交易組合的delta為0,這樣的交易組合被稱為delta中性(delta neutral)。
8.1.1 線性產品
線性產品的價值變化與標的資產的價值變化有某種線性關係(見圖8-1)。如果標的資產的價值是一項資產(如黃金)的價格,該資產的現貨頭寸顯然是一個線性產品。頭寸的價值與資產的價格呈線性關係。遠期是一種線性產品,而期權不是。
圖8-1 某種線性產品
線性產品的風險很容易對衝。例如,一家美國銀行與某企業做了一個遠期交易,在遠期合約中這家銀行同意在1年後以130萬美元的價格賣給這家企業100萬歐元。假定歐元和美元1年期的利率(每年複利1次)分別為4%和3%。這意味著,1年後100萬歐元的現值為1 000 000/1.04=961 538歐元,1年後130萬美元的現值為1 300 000/1.03=1 262 136美元。假定在當前1歐元等於S美元,合約價值(以美元計量)為[1]
1 262 136-961 538×S
這表明合約的價值和匯率S呈線性關係。合約的delta為-961 538,這家美國銀行可以通過買入961 538歐元來對衝風險。因為這一線性關係,delta對衝對匯率的大小變動都能提供保護。
假設銀行進入相反的交易,也就是說銀行在1年後必須買入100萬歐元,遠期合約價值為
961 538×S-1 262 136
合約的delta為+961 538,銀行可以賣空961 538歐元來對衝風險,即銀行首先以4%的利率借入歐元,並隨即將歐元轉換為美元,在1年後合約到期時,收到的歐元可以用於償還歐元貸款。
通過賣空資產以對衝遠期合約並不一定總是很容易實現的,黃金就是一個有意思的實例,金融機構時常發現自己需要進入大數目的遠期合約,而在合約中需要買入黃金,這意味著金融機構必須借入大量黃金以達到對衝效果。如業界事例8-1所示,中央銀行往往是銀行借入黃金的來源,中央銀行借出黃金會收一定的費用,這一手續費利率被稱為黃金租賃利率(gold lease rate)。
業界事例8-1
金礦企業的對衝決策
金礦企業擔心黃金價格會變化而採用對衝決策,這看來非常自然。通常金礦企業要花幾年時間來開採一個礦井中的所有黃金。當一個金礦企業準備開發某一金礦時,企業自然也就會對黃金價格有很大的風險敞口。如果黃金價格暴跌,那麼一個最初看來會盈利的金礦實際上會虧損。
金礦企業在向股東解釋其採用的對衝策略時往往非常謹慎。有些金礦企業不採用對衝來規避風險,這些企業會吸引那些想在黃金價格上漲中盈利,同時能承受黃金價格下跌帶來的損失的投資者。而有些金礦企業採用對衝來規避風險,這些公司對自己在今後幾年內每月能夠開採出的黃金產量有一個大概的估計,然後根據這一估計來賣空期貨或遠期合約,以鎖定賣出黃金的價格。
假設你代表高盛集團,你同某金礦企業進入了一個遠期合約,合約約定你要以一個指定價格買入很大數量的黃金,你將如何對衝你自己的風險呢?對這一問題的答案是:你會在中央銀行借入黃金,然後將黃金在現貨市場上變賣(一些有大量黃金儲備的國家的中央銀行都願意在收取一定的黃金租賃費用的前提下借出黃金)。在遠期合約到期時,你按照合約從金礦企業那裡買入黃金以償還從中央銀行處借入的黃金。
線性產品一個很有吸引力的特性是:對衝保護對標的資產價格的大小波動同樣有效。另一個同樣非常有吸引力的特性是:一旦建立了對衝,則在交易的有效期內,都不要再調整倉位(這一特性有時被稱作“保後即忘”(hedge and forget))。為了說明這一點,再次回顧一下我們上面的例子,銀行通過遠期合約,同意在1年後以130萬美元售出100萬歐元。為了對衝風險,銀行購入了961538歐元。銀行能夠以4%的收益投資這筆歐元,1年後,投資的本息合計恰好是100萬歐元。這正好就是銀行用來完成遠期合約交割所需要的數額。因此,在1年內,銀行都沒有必要對對衝倉位進行調整。
8.1.2 非線性產品
期權以及大多數結構性產品都屬於非線性產品,這些產品的價格(變化)同標的資產的價格(變化)有某種非線性關係,而這種非線性關係使得這些產品的風險更難被對衝。首先,將一個非線性的投資組合delta中性化只能在標的資產價格變化比較小時才起保護作用。其次,我們不能採取保後即忘的策略,而必須不斷地調整對衝倉位。這被稱作動態對衝(dynamic hedging)。
例如,一個交易員賣出100 000份歐式期權,標的資產為某種無股息的股票,市場及期權變量如下:
(1)股票當前市價為49美元;
(2)期權執行價格為50美元;
(3)無風險利率為5%;
(4)股價波動率為20%;
(5)期權期限為20周。
我們假定交易員因賣出期權而得到300 000美元收入,並且假定此交易員除了這一期權交易,他不持有和這一股票有關的其他交易。
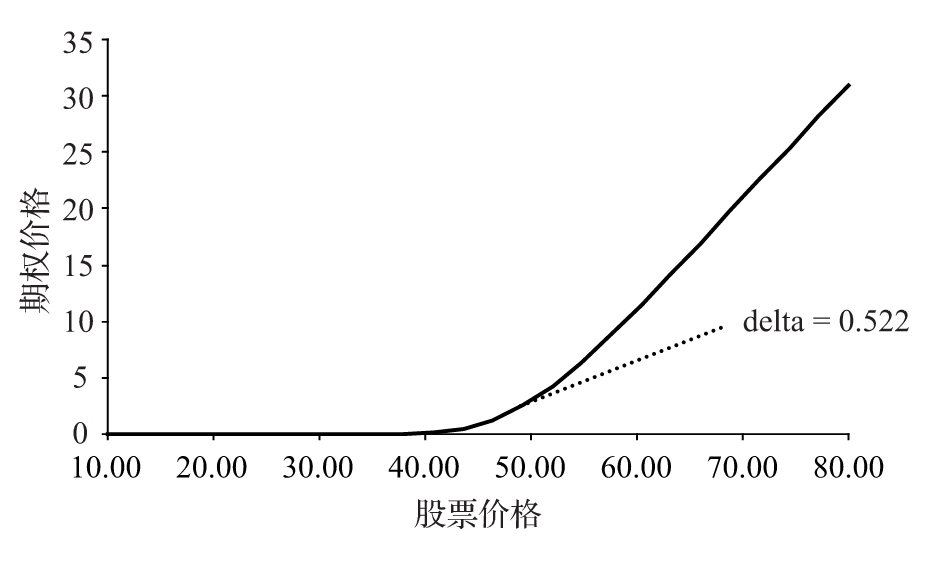
圖8-2 看漲期權價值與股票價格的變化關係
注:執行價格為50美元,無風險利率為5%,股價波動率為20%,期權期限為20周。
圖8-2顯示出期權價值與股票價格的函數關係。由於該函數是非線性的(即曲線),期權的delta取決於股票價格。當股票價格較低時,期權的價值幾乎為0,股票價格的微小變化導致的期權價值的美元增值也接近於0,這意味著期權的delta也接近於0。當股價較高時,比如70美元,看漲期權的買方會行權,因此期權的delta接近於1.0。這是因為股票價格中增加(減少)的ΔS使期權價值增加(減少)了ΔS。
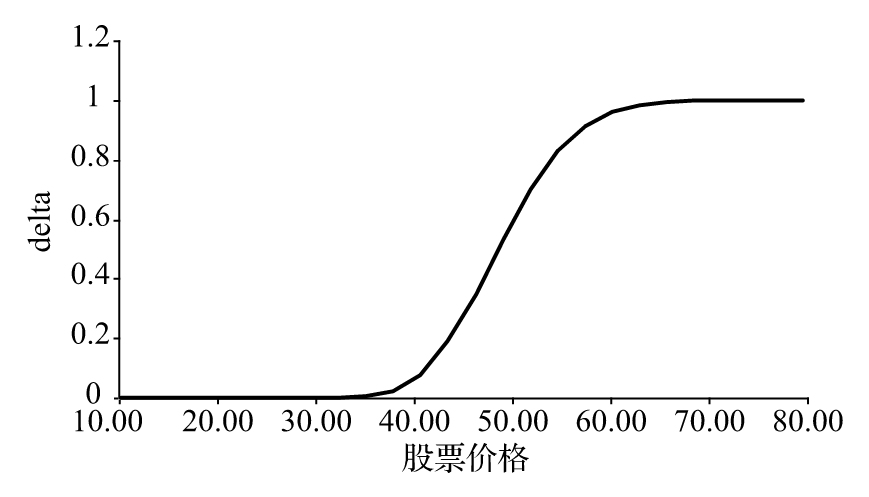
圖8-3 看漲期權的delta與股票價格的變化關係
注:執行價格為50美元,無風險利率為5%,股價波動率為20%,期權期限為20周。
在我們的例子中,股價為49美元,期權的delta是曲線在這一點上的斜率,在圖8-2中為0.522(有關歐式期權希臘值的計算見附錄E)。圖8-3顯示了一個期權的delta隨股票價格的變化關係。[2]在交易開始時,可買入1份標的股票的看漲期權的價值為2.4美元,而所對應的delta為0.522。因為該交易員賣出了對應100 000份的期權,所以交易員所持交易組合的價值為-240 000美元,交易組合所對應的delta為-52 200。交易員會因為期權的賣出價格超出了期權的理論價格60 000美元而感到興奮,但隨之而來的問題是如何對衝交易的風險以鎖定盈利。
賣出期權後,隨即買入52 200股股票可以使得交易組合達到delta中性。當股票價格有微小降低(增加)時,期權價值的收益(虧損)會被股票的損失(收益)中和。例如當股票價格由49美元漲到49.10美元時,期權價值會增加52 200×0.1=5 220美元,因此,期權的空頭會帶來5220美元的損失。這正好是股票價格上漲所帶來的收益。
對於線性產品,對衝交易在建立起來以後就無須調整。而對於非線性產品,為了保證delta中性,對衝交易要定期得到調整,這些調整過程被稱為再平衡(rebalancing)過程。
表8-2及表8-3顯示了在兩種不同情形下的再平衡模擬過程。假設對衝交易是每週進行一次。像我們在前面指出的那樣,最初的1份期權的delta為0.522,因而整個交易組合的delta為-52 200,這意味著在出售看漲期權的同時,交易員必須借入2 557 800美元並按49美元價格購買52 200股股票。借入資金的利率為5%,第1周的利息費用大約為2 500美元。
表8-2 delta對衝模擬,期權為實值期權,對衝成本為263 300美元
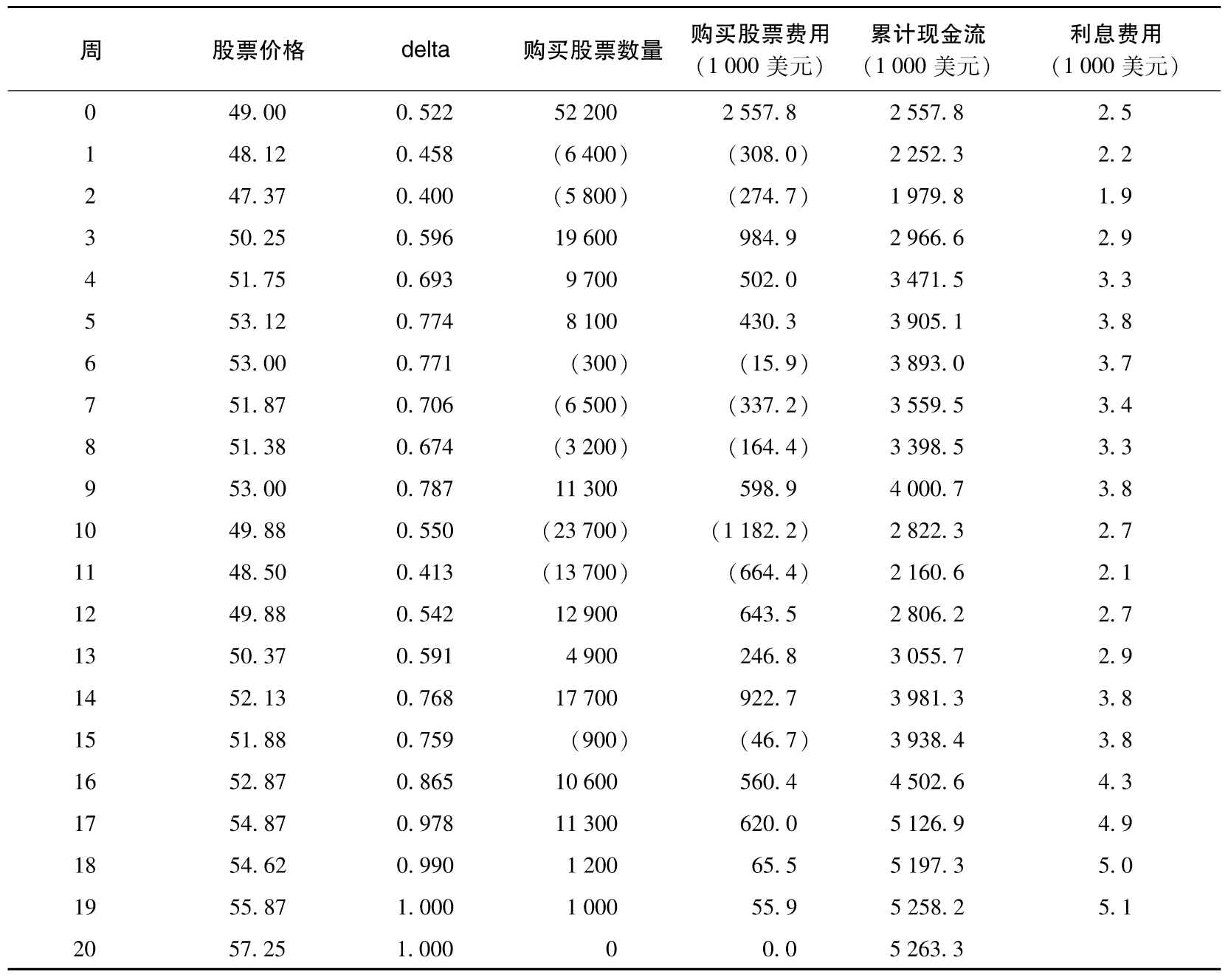
表8-3 delta對衝模擬,期權為虛值期權,對衝成本為256 600美元
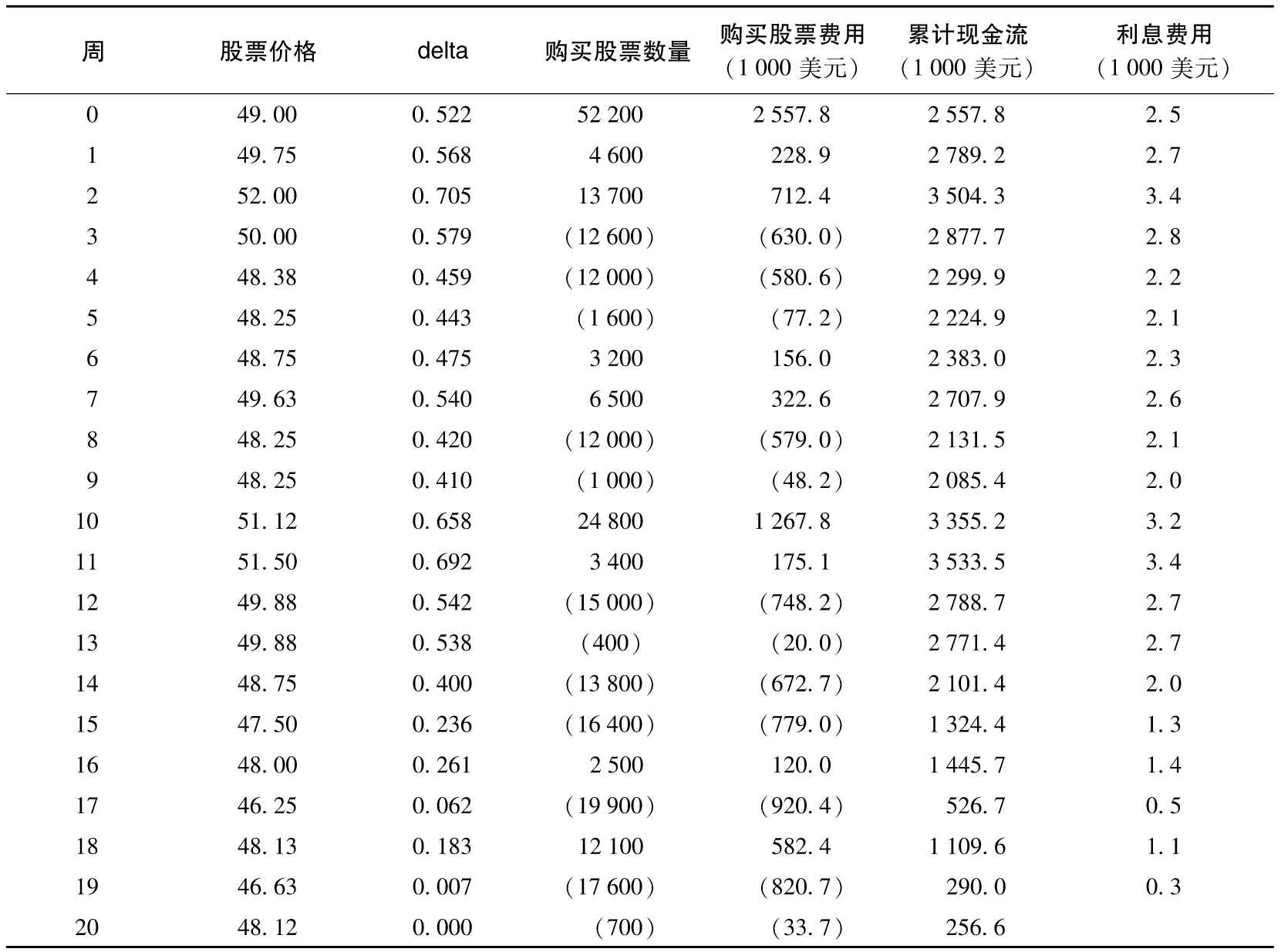
表8-2顯示,股票在1周以後價格降到了48.12美元,期權的delta也隨之降到了0.458。要保持delta中性,此時應該持有45 800股股票來對衝持有期權所帶來的風險,這意味著必須賣出6 400(=52 200-45 800)股股票,賣出股票帶來的現金收入為308 000美元,第1周的累計借款餘額減至
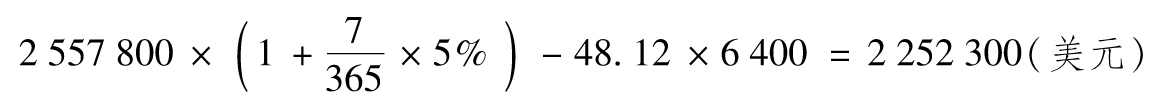
在第2周,股價繼續走低至47.37美元,期權的delta也隨之降低,保證delta中性需要再賣出5 800股股票。在第3周,股票價格上升到50美元以上,隨之delta會增加,這會造成在第3周結束時,需要買入19 600股股票。在期權接近到期時,很明顯期權將被行使,期權的delta接近於1.0。因此,在第20周結束時,對衝者會擁有100 000股股票,期權持有者會在此時行使期權,對衝者以執行價格賣出股票而收到5 000 000美元,賣出期權並對衝風險的總支出費用為263 300美元。
表8-3顯示出另一組模擬的股票價格,期權在到期時成為虛值期權,在第20周結束時,對衝者不持有任何股票,對衝總支出費用為256 600美元。
表8-2及表8-3顯示出,對衝成本的貼現接近於布萊克-斯科爾斯-默頓模型給出的理論價值240 000美元,並不完全一致。如果對衝機制是完美的,那麼在每一條股票價格的模擬路徑上,對衝成本的貼現值都應該與期權的理論價格完全相等。delta對衝成本與理論價值的差別是因為對衝交易頻率僅為一週一次,當對衝再平衡的頻率增大時,對衝成本與理論價值的差距會減小。當然,這裡的分析結果是建立在布萊克-斯科爾斯-默頓給出價格完全正確以及無交易費用等完美假設之下。
delta對衝的目的是儘量保證金融機構的交易組合價值恆定。開始時,賣出期權價值為240 000美元。如表8-2所示,第9周時的期權價值為414 500美元,因而金融機構因賣出期權損失174 500美元(=414 500-240 000)。累計現金費用在第9周時比交易開始(第0周)時要多1 442 900美元,所持有的股票的價格由最初的2 557 800美元變為4 171 100美元,增加了1 613 300美元。將所有因素彙總在一起,到第9周,金融機構的交易組合價值變化僅僅為4 100美元。
8.1.3 費用由何而來
由表8-2及表8-3所示的delta對衝機制以合成的形式構造出一個期權的多頭,而這一“合成”期權會被用來對衝交易員的期權空頭交易。正如表中所示,對衝機制會造成股價下跌後賣出股票,而在股價上升後買入,這正是所謂的“買高賣低”。240 000美元的費用來自購買股票的價格與賣出價格之間的平均差價。
8.1.4 交易費用
按以上描述方式維持一個由單一資產為標的的期權和資產本身組成的組合的delta中性而引發的交易費用會非常昂貴,以至於對交易員來說不具可操作性。但對一個由多種衍生產品組成的大的交易組合,如果這些衍生產品的標的是同一個資產,則維持delta中性的可操作性會更好,因為將整個組合的delta歸零,只需要進行一筆標的資產的交易即可。因此交易費用會更容易地被其他交易的利潤所吸收。這表明,衍生產品交易也具有規模效應,因此衍生產品市場被少數幾家大的交易商所控制也就不足為奇了。
[1] 關於遠期合約的定價,見附錄C。
[2] 圖8-2及圖8-3是由軟件RMFI產生的,這一軟件可在作者的網頁上下載,計算中採用了布萊克-斯科爾斯-默頓解析模型,讀者可選擇“Black-Scholes-European”。