e1 John Hull 風險管理與金融機構 v5
7.6 對真實世界中的過程進行估計
在情景分析中,我們面臨的一個主要問題是,我們對市場變量在風險中性世界中表現的瞭解,常常遠多過對它們在真實世界中表現的瞭解。考慮一隻股票的價格,我們知道在風險中性世界,股價的回報就是無風險利率。我們可以從歷史數據或以該股票作標的的期權價格中計算出波動率。對於消費資產(即非純粹用於投資的資產),期貨價格可用於提供有關其價格在風險中性世界中預期表現的信息。類似地,利率期限結構提供了風險中性世界中利率遵循的規律信息。
不幸的是,在真實世界中不存在這類隱含計算的方法。理論上,我們可以從歷史數據中推導。但在實際中,要得出比較準確的估計所需要的歷史數據量是很大的(遠遠超過得出合理波動率所需要的數據量)。
我們還可以使用資本資產定價模型(見第1章)。我們可以先估計這隻股票的回報與某個對整個市場有代表性的指數(如標準普爾500指數)的表現的相關係數ρ。如我們在第1.3節中解釋的,這隻股票的β可由下式計算出
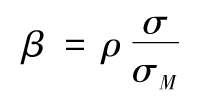
其中,σ是股票回報的波動率,σM是標準普爾500指數回報的波動率。根據資本資產定價模型,股票在真實世界中的回報率為
RF+βE
其中,RF是無風險利率,E是市場相對於無風險利率的預期超額回報(通常假設為5%或6%)。
我們可以對其他變量使用類似的方法。假設一個市場變量的波動率是σ(注意波動率在真實世界和風險中性世界中是相同的)。該變量在真實世界中的百分比變化量超出其在無風險世界中的變化量可計為λσ,其中λ被稱作該變量風險的市場價格。一般來說
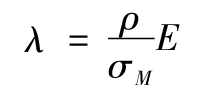
其中ρ為該變量百分比變化量與標準普爾500指數回報的相關係數。
現在考慮某一商品的價格。如果它的回報和標準普爾500指數的回報沒有相關性,我們可以假設它在真實世界中的預期回報和在風險中性世界是相等的。或者,設ρ=0.3,σM=0.2,E=0.06,我們可以推算出λ=0.09。如果商品價格的波動率是40%,則其回報率應為0.09×0.40=3.6%,即在真實世界中的預期回報高於風險中性世界中的回報。
就利率而言,市場風險價格為負(通常在-0.1至-0.2)。[1]這意味著,在風險中性的世界,利率的增長速度要快於真實世界(這使得利率不同於股票價格,而在真實世界中恰恰相反)。
[1] 參見J. Hull, A. Sokol, and A. White, “Short-Rate Joint-Measure Models,” Risk (October 2014): 59-63,以獲得估算利率風險市場價格的方法。美國聯邦儲備委員會有時會根據經驗判斷實際利率的變動幅度是每月比實際利率低一個基點。