e1 John Hull 風險管理與金融機構 v5
7.5 實踐中的計算
我們剛剛看到的例子非常簡單,因為組合中只有一個金融工具——一個2年期的股票遠期。我們知道該合約的價值隨著標的股票價格的上升而下降。當該股票的價格達到概率為1%的高點時,遠期合約的價值就會跌到概率為1%的低點。
在實踐中,一家金融機構的投資組合通常包括大量的金融工具,因此進行情景分析需要的計算可能會非常複雜。要了解自今天起始的特定時間段內真實世界中可能發生的情況,我們需要生成大量的場景,並在這些場景下對投資組合進行定價。然後,我們才能知道在某一概率下(例如1%)所對應的損失的情況。舉例而言,如果我們考慮了1 000個場景,1%概率對應的損失就是這些場景中出現的第10個的損失。
對股票價格、股指價格和匯率等市場變量,最常用的模型一般會假設預期增長率μ和波動率σ是兩個常數,或是時間的某個函數。由式(7-1)可知,如果St是市場變量在時間t的值,我們有
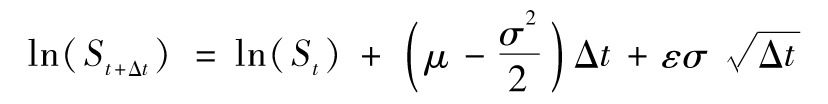
其中,ε是一個服從標準正態分佈的隨機變量(均值為0,波動率為1)。也就是說
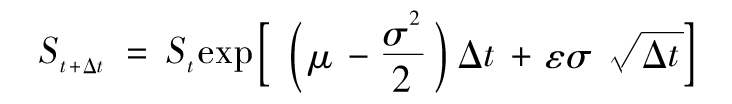
通過這個公式,我們就可以從一個標準正態分佈中取樣,以Δt為時間步長對一個市場變量進行模擬。
短期利率、波動率和商品價格等市場變量使用的模型會更加複雜。這類模型不僅考慮變量表現出的波動性,而且還假設從長期來看變量會迴歸到一個平均水平。這一現象被稱作均值迴歸(mean reversion)。在大多數情況下,我們並不假設各種市場變量的變動是相互獨立的。市場變量之間的相關性通常可以通過歷史數據估算出來。然後,這些相關性可以通過標準正態分佈隨機變量ε之間的相關性體現出來(我們在第11章中介紹特定相關係數下的多元標準正態分佈取樣的方法)。
從上面這個簡短的介紹中我們可以看出,情景分析可能非常耗費時間。在每次模擬中,除要通過取樣生成市場變量的值以外,還需要計算組合在所模擬的時間點上的價值。網格計算技術(grid computing,一種調度多個計算機資源協同工作,以完成同一個任務的分佈式計算技術)常常被用來進行這類計算。有時,為了能在合理的時間內得到結果,我們還不得不對蒙特卡羅模擬實驗的次數進行限制。