BUSINESS BOOKS

7.3　情景分析

現在我們討論情景分析。在情景分析中，我們希望瞭解將來可能發生的狀況。我們的目的不是定價，而未來的現金流也不會貼現到當前。在進行情景分析時，我們考慮的世界是真實世界，而不是風險中性世界。我們要強調的是，風險中性世界不過是我們為了對衍生產品進行定價而構造的一個人造的世界而已。對風險管理人員來說，他們一般不會太關心在一個人人都是風險中性的虛擬世界中，將來會發生什麼情況。

使用哥薩諾夫定理（Girsanov’s theorem），我們可以比較簡便地在真實世界和風險中性世界中切換。該定理證明，當我們從某一種風險偏好設定的世界變換到另一種風險偏好設定的世界時，市場變量，如股票價格、商品價格、匯率和利率的預期增長率會發生變化，但是它們的波動率不會變。

為說明情景分析是如何進行的，假設真實世界中的股票預期回報率為8%，目前股價為30美元，其波動率為25%。若你擁有10 000股股票，明年你的損失額會是多少？

由式（7-5）可知，在真實世界中1年內股票價格分佈的5%分位數為

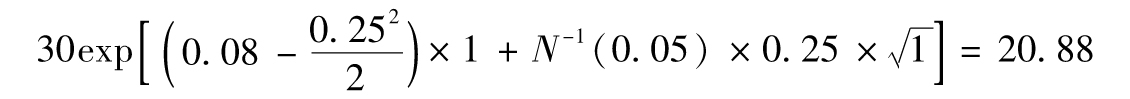
類似地，股票價格分佈的1%分位數是17.61美元。

因此，有95%的概率在接下來的1年裡損失不會超過10 000×（30-20.88）=91 200美元。同樣，可以99%地確定損失不會超過123 900美元。我們將在後面的章節中看到，這些就是所謂的風險價值評估。

這裡的關鍵是，由於我們在進行情景分析而不是評估，所以該結果是基於真實世界的預期回報率，而不是無風險回報率。