BUSINESS BOOKS

7.2　風險中性定價

衍生產品定價最重要的一個手段就是風險中性定價。一個風險中性世界（risk-neutral world）可以是一個想象中的世界，在這個世界中投資者不要求為所承擔的風險得到補償。也就是說，在該世界中，一項有風險的投資需要提供的預期回報與無風險的投資是一樣的，均為無風險利率。我們生活的真實世界顯然不是風險中性的。我們身邊的投資者均要求為自己承擔的風險獲得補償（第1章給出了一個便於理解風險-回報替代關係的框架）。但是，風險中性定價方法顯示我們可以通過假設世界是風險中性的來為任何衍生產品定價，而且我們不僅可以在風險中性世界中得出正確的定價結果，該結果還可以用在任何其他世界中。

乍看上去，風險中性定價的結果似乎完全不合理。投資者並不是生活在風險中性的世界中。當他們面對的風險上升時，他們通常會要求得到更高的回報，這一結論適應於衍生產品及其他投資。^[1]但當我們試圖理解風險中性定價時，需要注意關鍵一點，對某一衍生產品進行定價，我們計算的價格是與標的資產價格有關（例如，股票期權價值的計算與標的股票的價格有關），而標的資產的價格反映了市場參與者對風險-回報的權衡。如果市場參與者認為由於資產的風險他們應該獲得更多（更少）的回報，資產的價格就會下降（上升）。而風險中性定價認為將標的資產價格轉換成衍生產品價格的計算公式是獨立於投資者的風險偏好的。

在風險中性世界中，所有未來的現金流都以無風險利率進行貼現。這極大地簡化了定價。假設我們要給一隻股票的看漲期權定價，無風險利率是3%。風險中性定價的步驟如下：

（1）假設股票未來的預期回報率是3%（平均值）；

（2）計算看漲期權的預期收益；

（3）以3%的貼現率將預期收益貼現，得到期權的當前值。

一個很自然的問題是：“既然在真實世界中定價更為自然，為什麼我們還需要風險中性世界？”答案在於，雖然在理論上我們可以在真實世界中對一個看漲期權進行定價，但在實踐中這樣做很困難。我們需要履行以下的步驟：

（1a）估計股票在真實世界中的預期回報率（平均值）；

（2a）計算真實世界中看漲期權的預期收益；

（3a）以適當的貼現率將期權的預期收益貼現，作為期權的當前價值。

在步驟（1a）中，我們有可能得到一個合理的、在真實世界中的股票未來預期回報率。為此，我們需要估計股票的beta，並使用第1章中介紹的資本資產定價模型。但完成步驟（3a）將非常困難。用來對真實世界預期收益進行貼現的正確貼現率依賴於期權的（而不是股票的）beta，而這個值在期權的生命週期中很有可能是變化的。隨著股票價格的變化，期權中隱含的槓桿會發生變化，貼現率也會跟著變化。如果在看漲期權的整個生命週期中使用單一貼現率，那麼得出的期權價值會非常高；同樣地，如果在一個看跌期權的生命週期中使用單一貼現率，那麼得出的期權價值會非常低，通常是負值。我們是怎麼知道這些情況的？我們可以使用風險中性定價，算出期權的價值，然後從這個答案倒推，看看要得到同樣的答案，在真實世界中正確的貼現率應為多少。後面我們會以一個二元期權為例，說明這一點。

風險中性定價是一個看上去很神奇的結論。它意味著我們無須關心諸如衍生產品的風險大小和市場對標的資產及衍生產品的回報要求之類的問題。我們需要問自己的唯一的問題是：如果我們生活在一個投資者對任何投資所要求的回報均等於無風險利率的世界中，我們如何對衍生產品進行定價？如果沒有風險中性定價，衍生產品的定價將會更加複雜（而且更加不準確）。

需要強調的是，風險中性定價（或者說“投資者在決定投資的預期回報時，並不關心投資的風險”這一假設）只不過是用來給衍生產品定價的一種人工設備。從中得到的定價結果不僅在風險中性世界中是正確的，在其他所有世界中也是正確的。當我們從風險中性世界變化到真實世界中時，會同時發生兩件事情：衍生產品的預期收益會發生變化，同時用於對預期收益進行貼現的貼現率也會發生變化。這兩個變化總是恰好相互抵消。

7.2.1　在遠期合約中的應用

作為風險中性定價的一個簡單例子，讓我們考慮一個遠期合約的多頭的定價，合約的標的資產是一隻不付股息的股票。假設交割價為K，期限為T。在到期日，合約的價值為

S_T-K

其中S_T是股票在T時刻的價格。根據風險中性定價的論點，該遠期合約在當前時刻（即零時刻）的價值即為它在風險中性世界中T時刻的價值以無風險利率貼現後的值。設遠期合約的價值為f，我們有

f=e^-rTÊ（S_T-K）

其中Ê表示無風險世界中的期望值，r為無風險利率（假設為常量）。因為K為常量，我們有

f=e^-rTÊ（S_T）-Ke^-rT

（7-6）

在無風險世界中，股票價格的增長率是r。由此我們得到

Ê（S_T）=S₀e^rT

其中S₀為股票的當前價格。將上式代入式（7-6）中

f=S₀-Ke^-rT

（7-7）

類似地，遠期合約空頭的價值為

Ke^-rT-S₀

（7-8）

上述結果和附錄C中的結果是一致的。

7.2.2　在二元期權合約中的應用

在本節中，我們給出了一個風險中性定價的更進一步的例子。假設一隻不付股息的股票的價格是30美元，如果1年後股價高於40美元，某衍生產品就會支付100美元。這種衍生產品被稱為二元或指狀（digital）或者是現金或無價值（cash-or-nothing）期權。假設無風險利率為每年3%（連續複利），真實世界中股票的預期增長率是每年10%（同樣是連續複利），股票的年波動率為30%。

在風險中性世界中，股票的預期增長率是每年3%。股票價格在1年後高於40美元的風險中性概率可以通過計算得出：設式（7-3）中的參數μ=0.03，T=1，σ=0.3，S₀=30，V=40。我們有

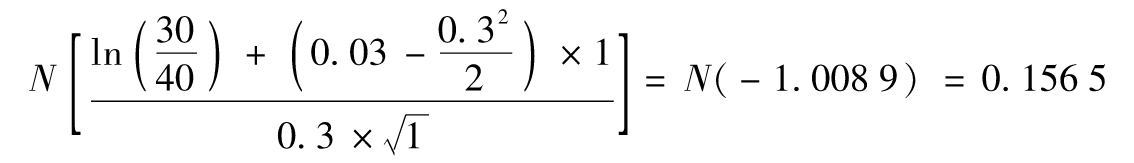
在風險中性世界中，該衍生產品的預期收益為100×0.1565=15.65美元。衍生產品的價值按3%無風險利率貼現1年後的價值為15.65e^-0.03×1=15.19美元。

真實世界中股票價格在1年後高於40美元的概率是這樣來計算的：設式（7-3）中μ等於假定的股票1年後的回報10%，得出的概率為0.2190（我們將在本章後面的內容中解釋，當從風險中性世界變換到真實世界時，不需要改變波動率；反之亦然）。因此在真實世界中，期權的預期收益是21.90美元。我們前面曾經提到過，使用真實世界的預期收益進行定價的問題在於我們不知道應該使用什麼樣的貼現率。股票的價格存在風險，該風險已經被市場定價（否則股票的預期收益就不會是高於無風險利率的7%）。衍生產品可以在該風險基礎上增加槓桿，因此對衍生產品的預期收益貼現時應該使用更高的貼現率。我們知道該衍生產品正確的當前價值應為15.19美元，據此我們可以推算出真實世界中21.90美元的預期收益應使用的貼現率為36.6%（這是因為21.90×e^-0.366×1=15.19）。

7.2.3　布萊克-斯科爾斯-默頓公式的應用

接下來我們考慮一隻不付股息的股票的歐式期權，執行價格為K，到期日為T，假設無風險利率為r，在T時刻的收益為

max（S_T-K, 0）

其中S_T為股票在T時刻的價格。因此，期權在T時刻的預期收益是

Ê［max（S_T-K, 0）］

其中Ê表示風險中性世界中的期望值。使用風險中性定價的結論，該期權的價值為

e^-rTÊ［max（S_T-K, 0）］

（7-9）

類似地，相應的看跌期權的價值為

e^-rTÊ［max（K-S_T, 0）］

在進行一些代數變換後，我們可以證明這些結論可以推導出附錄E中的布萊克-斯科爾斯-默頓公式，用於歐式股票期權的定價。^[2]

7.2.4　應用於離散化回報的情況

風險中性定價還可以用於回報是離散化的情況。假設在T時刻可能出現兩種互斥的結果。設π₁為某衍生產品的價值，如果第一種結果出現，那麼該衍生產品在T時刻的收益為1美元，否則收益為0。同樣地，設π₂為另一個衍生產品的價值，如果第二種結果出現，那麼該衍生產品在T時刻的收益為1美元，否則收益為0。如果同時買入這兩個衍生產品，那麼我們可以保證在T時刻獲得1美元的收益。在T時刻保證獲得的1美元收益的當前價值為e^-RT，其中R為到T時刻的無風險利率（連續貼現）。所以我們有

π₁+π₂=e^-RT

（7-10）

現在考慮另一個衍生產品，如果在T時刻第一種結果發生，則該產品支付V₁；如果第二種結果發生，則支付V₂。該衍生產品的價值為

π₁V₁+π₂V₂

進一步有

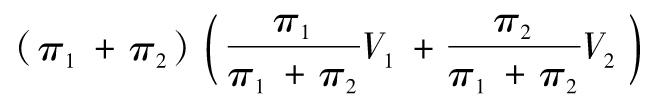
將式（7-10）的結果代入上式，該衍生產品的價值為

e^-RT（p₁V₁+p₂V₂）

其中

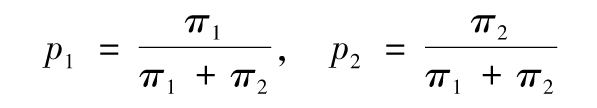
從這個結果出發，我們可以很自然地把p₁和p₂看作是兩種結果分別發生的風險中性概率。該衍生產品的價值也就是其在風險中性世界中預期收益以無風險利率的貼現。這個例子說明風險中性定價也適用於結果是離散的情形。

上述結果還可以擴展到結果有很多種可能的情況。假設在T時刻可能會發生n種互斥的可能的結果。設π_i是一個衍生產品的價值，該衍生產品在第i（1≤i≤n）種可能結果發生時，收益為1美元，否則為0。那麼，一個在第i（1≤i≤n）種可能結果發生時，收益為V_i美元的衍生產品的價值為

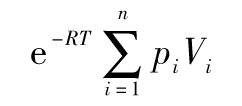
其中，p_i為第i（1≤i≤n）種可能結果發生的風險中性概率，且

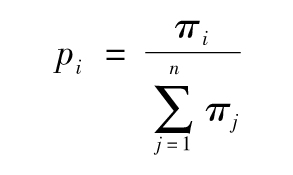
7.2.5　應用於違約概率

考慮一個金融工具，其回報取決於某家公司是否違約（這樣的工具可以定義成信用衍生產品）。根據我們在前面所做的分析，如果我們要對這樣一個衍生產品定價，那麼可以遵循以下步驟：

（1）估計違約的風險中性概率；

（2）計算衍生產品的預期收益；

（3）將預期收益按無風險利率貼現。

我們將在第19章中看到，風險中性違約概率可以由該公司發行的債券的收益率或信用違約互換利差推出。一般來說，風險中性違約概率會高於真實世界中的違約概率。

[1] 如在第1章中解釋的，對投資者來說系統性（即不能被分散的）風險是至關重要的。

[2] 按照約翰·赫爾所著的《期權、期貨及其他衍生產品》（Options, Futures, and Other Derivatives, 10th ed, Upper Saddle River, NJ: Pearson, 2018），可用三種方式推導出布萊克-斯科爾斯-默頓公式。第一種是先建立滿足所有衍生產品的微分方程，然後通過恰當的邊界條件求解；第二種是建立股票價格行為的二叉樹，然後對時間步長取極限，使其趨向於0；第三種是通過式（7-9）。這種方式的詳細步驟可在本書附錄和《期權、期貨及其他衍生產品》（原書第10版）的第15章中找到。