e1 John Hull 風險管理與金融機構 v5: 7.1 波動和資產價格

e1 John Hull 風險管理與金融機構 v5

在討論定價和情景分析之前，我們先來介紹幾點與資產價格的表現有關的常用知識。假設資產的當前價格為S₀，一個常見的假設是價格每年會以一個常量μ（以連續複利計）增長，價格的波動率也是一個常量，每年為σ。^[1]我們可以證明，在T年後，資產價格S_T的概率密度函數為^[2]

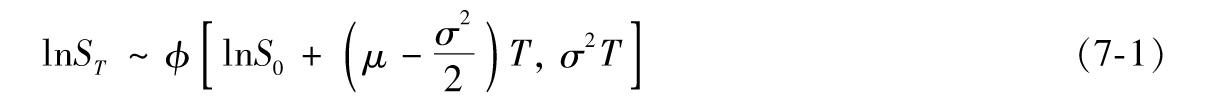
其中，ϕ（m，v）表示均值為m、方差為v的正態分佈，ln為自然對數函數。變量S_T服從對數正態分佈，因為它的自然對數是一個正態分佈。lnS_T的均值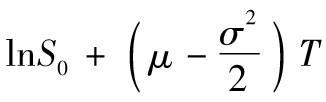是，標準差是。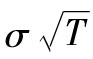

S_T小於某個值V的概率，等於lnS_T小於lnV的概率。根據正態分佈的性質，我們可以得到

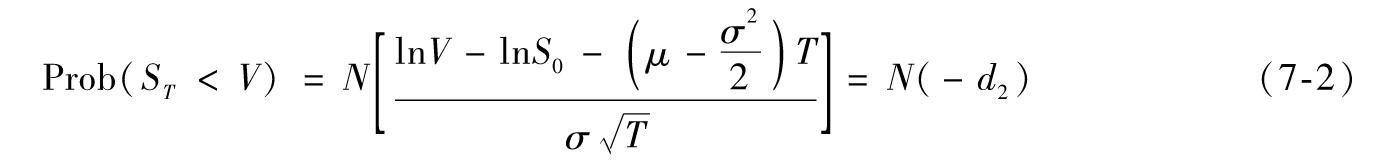
其中

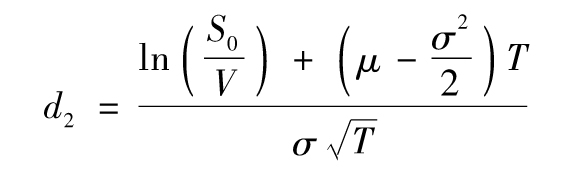
N為正態累積分佈函數，可由Excel軟件中的NORMSDIST函數計算得出。在T時刻，S_T大於V的概率為

Prob（S_T>V）=1-N（-d₂）=N（d₂）

（7-3）

最後，假設我們希望找到V，使得S_T的值大於V的概率是q，也就是說Prob（S_T>V）=q。由式（7-3），我們有N（d₂）=q，即

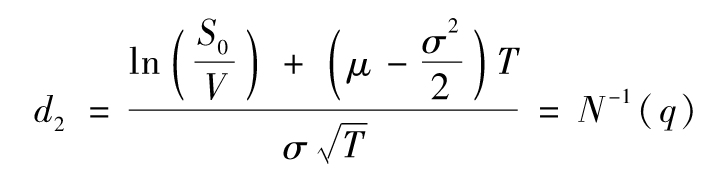
或者

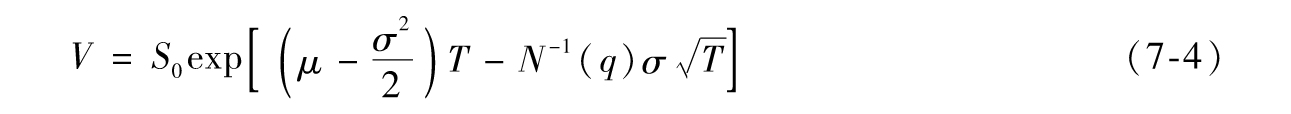
其中N^-1是正態累積分佈函數的反函數，可由Excel的NORMSINV函數算出。類似地，若S_T的值小於V的概率是q，即Prob（S_T<V）=q，由N（-d₂）=q或d₂=-N^-1（q），可知

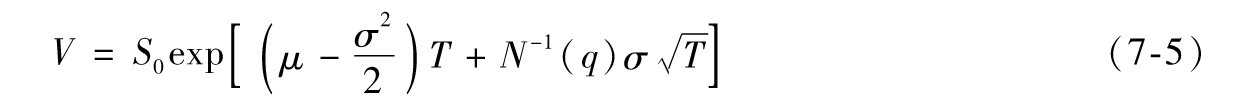
[1] 我們在附錄A中對於連續複利做了介紹。顧名思義，波動率是一個度量股票價格不確性的手段，在第10章中我們將對它進行更精確的定義。

[2] 推導過程可見J. Hull, Options, Futures, and Other Derivatives, 9th ed. (Upper SaddleRiver, NJ: Pearson, 2015)。