e1 John Hull 風險管理與金融機構 v5
3.3 死亡率表
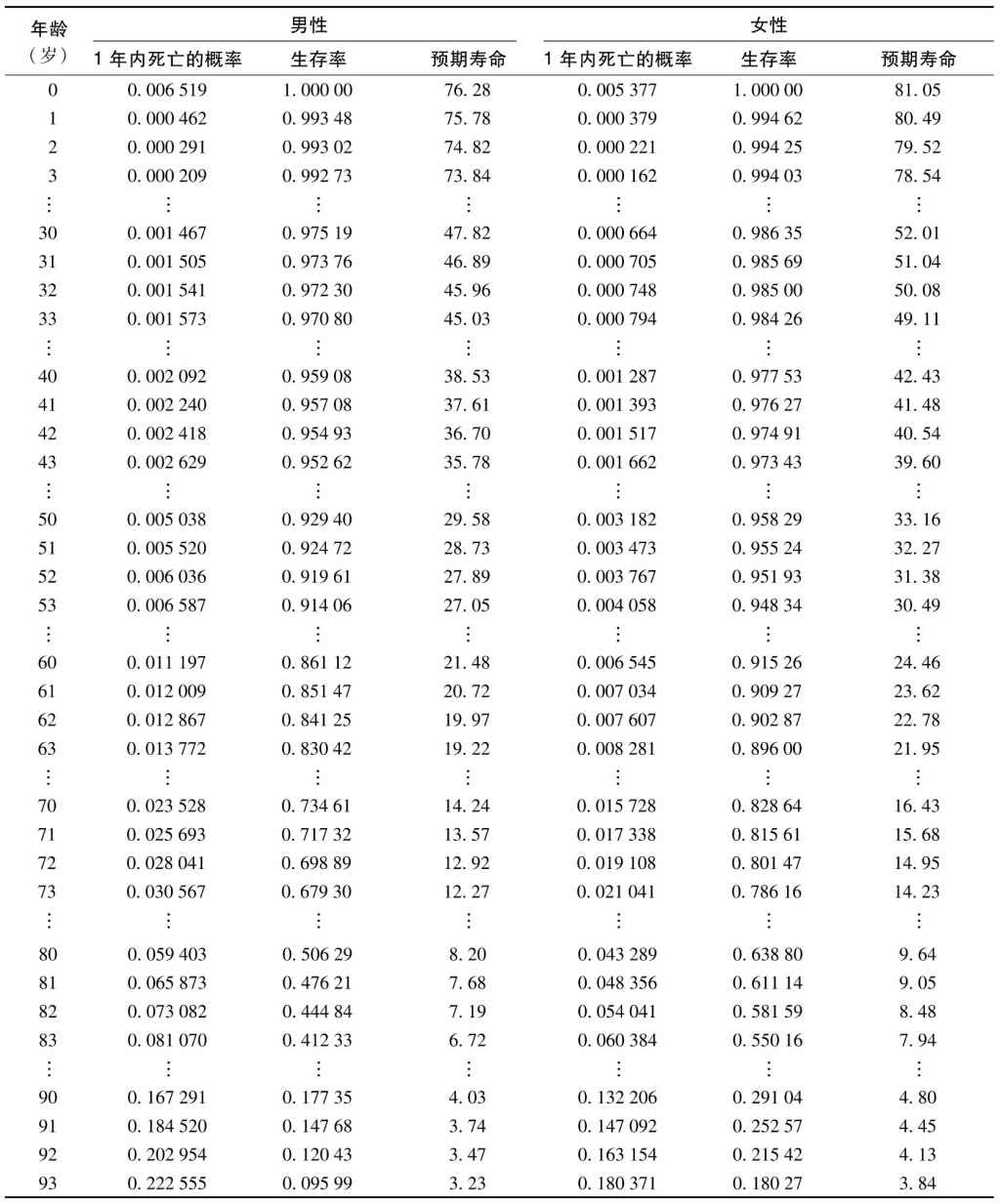
死亡率表是人壽保險合約定價的關鍵,表3-1是美國社會保障部(Department of Social Security)給出的2013年的人類死亡率表。為了理解這一表格,我們考慮對應於年齡為31歲的一行,表中第2列顯示一個31歲男性在1年內死亡的概率為0.001505(即0.1505%)。第3列顯示了一個男性能夠活到31歲的概率為0.97376(即97.376%)。第4列顯示一個31歲男性的剩餘預期壽命(remaining life expectancy)[1]為46.89年。這意味著平均來講,一個男性的預期壽命為77.89歲。表中的其他3列是關於女性的數據,一個31歲女性在一年內死亡的概率為0.000705(即0.0705%),一個女性能活到31歲的概率為0.98569(即98.569%),31歲女性的剩餘預期壽命為51.04年。
表3-1 死亡率表
資料來源:美國社會保障部,www.ssa.gov/OACT/STATS/table4c6.html.
表格數據顯示,在生命的前10年,一個人在下一年死亡的概率是年齡的遞減函數;在10年之後,死亡的概率是年齡的遞增函數。女性的死亡率數據比男性好看一些,如果一位男性能活到90歲,他在下一年的死亡概率為16.7%;數據還顯示當男性活到100歲時,他在下一年死亡的概率為35.4%;活到110歲時,下一年死亡的概率為57.6%。對於女性而言,相應的概率為13.2%、30.5%及54.6%。
表3-1中的所有數據都可以從“一年內死亡的概率”這一列中的數據計算出來。一個人活到n+1歲的概率是這個人活到n歲的概率與1減去一個n歲的人在下一年內死亡的概率的乘積。例如,男性活到61歲的概率可以計算為0.861 12×(1-0.011 197)。
接下來考慮某個年齡段的人的預期壽命。這可以根據第1年、第2年、第3年以及往後年份的死亡概率來確定。從表3-1中來看,一個現年90歲的男性在1年內死亡的概率是0.167 291。他在第2年(介於91歲和92歲之間)死亡的概率等於他在第1年仍然活著的概率乘以他在91歲後1年內死亡的概率。根據表格第2列的數字,可以表示為
(1-0.167 291)×0.184 520=0.153 651
類似地,一個現年90歲的男性在將來的第3個年間(即介於92歲和93歲)死亡的概率為
(1-0.167 291)×(1-0.184 520)×0.202 954=0.137 817
假設死亡平均發生在每年的年中,一個90歲男性的預期剩餘壽命為
0.5×0.167 291+1.5×0.153 651+2.5×0.137 817+…
【例3-1】 假定對應於所有期限的利率均為4%(每半年付息一次),保險的保費在年初時支付,為一個具有平均健康狀態的90歲男性投保一個保額為100 000美元的人壽保險的盈虧平衡保費(break-even premium)為多少?假定保險期限為1年,預期賠償值為0.167 291×100 000,即16 729美元。假定賠償支付時間在年正中(在平均意義上,這是一種準確的估計);保費等於預期賠償以6個月的利率進行貼現得到的當前值,我們已知貼現利率為4%,利率一年複利兩次,賠償值的貼現值等於16 729/1.02,即16 401美元。
接下來假定保險的期限為2年,在第1年的預期賠償貼現值如上所述,即為16 401美元。受保人在第2年死亡的概率為(1-0.167 291)×0.184 520=0.153 651,因此在第2年的預期賠償為0.153 651×100 000=15 365美元。假定賠償支付時間在第18個月,預期賠償的貼現值為15 365/1.023=14 479美元。因此整體預期賠償的貼現值為16 401+14 479=30 880美元。
接下來我們計算保費的支付。首先我們知道第1次保費一定會在第1年年初被支付;第2次保費在第2年發生的概率為男性在第1年內仍然生存的概率,即1-0.167 291=0.832 709。如果保費數量每年為X,所有保費支付的貼現值等於
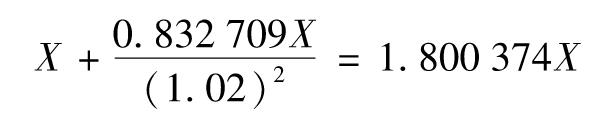
盈虧平衡保費X會保證預期保費支付的貼現值等於預期賠償的貼現值,即
1.800 374X=30 880
即X=17 152,因此盈虧平衡保費為17 152美元。
[1] 即在給定年齡下,一個人繼續生存的年限。——譯者注