e1 John Hull 風險管理與金融機構 v5
1.3 資本資產定價模型
當投資者投資於某些資產時,他們如何判定自己需要的預期回報呢?我們的以上分析說明,市場投資組合會起一個決定性的作用,投資者對於某資產回報所需要的預期回報在一定程度上要反映此資產對市場投資組合風險的奉獻量。
一個較常用的方式是以投資資產的回報及市場投資組合回報的歷史數據來得出某種最佳線性迴歸關係。這種線性迴歸關係式可表達為
R=α+βRM+ε
(1-3)
其中R代表投資資產的回報,RM代表市場投資組合的回報,α和β都是常數,ε是指回歸誤差,為隨機變量。
式(1-3)顯示了除了常數項α以外,資產回報有兩個組成部分。
(1)一部分對應於βRM,此項為市場投資組合回報的某種倍數。
(2)另一部分對應於ε,此項與市場投資組合的回報無關。
這裡對應的風險,第一部分被稱為系統性風險(systematic risk),而第二部分被稱為非系統性風險(nonsystematic risk)。
首先讓我們考慮非系統性風險。如果我們假定對應於不同投資資產的ε項相互獨立,在大型投資組合中,非系統性風險幾乎被分散殆盡,因此投資者不應該關心非系統性風險,也就是說投資者不應該因承擔非系統性風險而索取高於無風險利率之上的回報。
系統性風險是投資者應該關心的內容,當持有一個大型而風險分散均衡的投資組合時,由βRM表示的系統性風險並沒有消失,因此承擔這一系統性風險,投資者應索取補償。
由圖1-4可知,我們可以看到預期回報與系統性風險之間的關係,β=0對應於非系統性風險,其所對應投資回報為RF。當β=1時,投資資產的回報與M點對應,此時的預期回報為E(RM)。一般來講,我們有關係式
E(R)=RF+β[E(RM)-RF]
(1-4)
式(1-4)就是所謂的資本資產定價模型,這一公式說明某投資的預期回報超出無風險投資回報的數量等於市場投資組合的預期回報超出無風險投資回報的數量與β的乘積。圖1-5中顯示了這一關係式。參數β被稱為是投資的β係數。
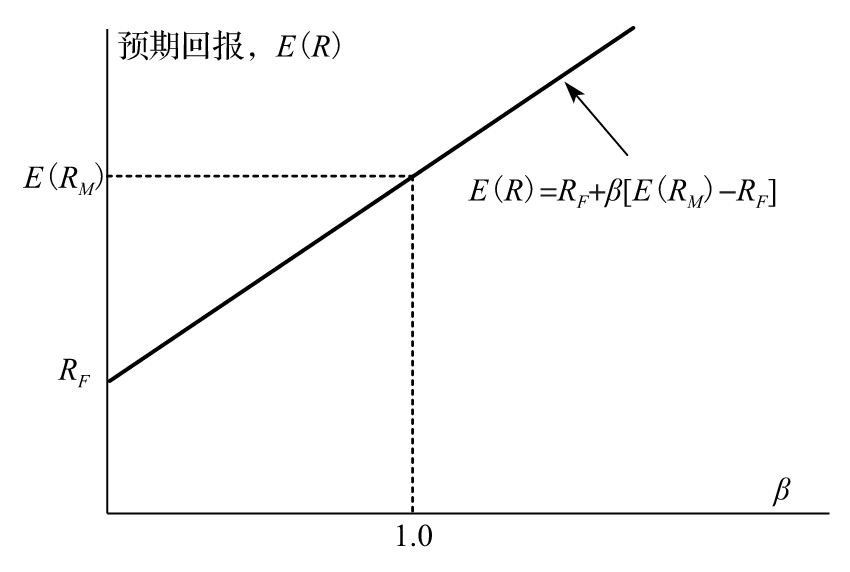
圖1-5 資本資產定價模型
【例1-1】 假定無風險投資利率為5%,市場投資的預期回報率為10%。如果一項投資的β為0,那麼該投資的預期回報為5%,這是因為投資中的風險可以被完全分散;如果一項投資的β為0.5,那麼該投資的預期回報為
0.05+0.5×(0.1-0.05)=0.075
即7.5%;如果一項投資的β為1.2,那麼該投資的預期回報為
0.05+1.2×(0.1-0.05)=0.11
即11%。
係數β被稱為投資組合的beta係數,等於ρσ/σM,其中ρ是投資資產與市場投資組合的相關係數,σ是指投資資產回報率的標準差,σM是市場投資組合回報率的標準差,beta係數體現了投資組合對於市場投資組合的敏感性,我們可以用式(1-3)來定義任何一種投資組合的beta係數,而資本資產定價模型式(1-4)中對應於這一投資組合的回報率R。在圖1-4中,由M點所代表的市場投資的beta係數為1.0,由F點所代表的無風險投資的beta係數為0,而由I和J所代表的投資資產的beta係數分別為βI及βJ。
1.3.1 假設
以上分析帶給了我們一個驚人的結論,那就是所有的投資者均想持有一個同樣的投資組合(即圖1-4中M點所表示的投資組合),這一結論顯然不成立。如果以上結論成立,那麼投資者相互之間不會再進行交易,市場也會停止運作。在實際中,不同的投資者對於股票及其他風險投資產品有著不同的看法,正因為如此,投資者之間才相互進行交易,從而促成了市場價格的產生。
在以上分析中,我們採用了多個隱含假設,這些假設造成了其得出的結論與現實市場有所出入。假設包括:
(1)我們假設投資者只關心他們投資組合的預期回報及回報率的標準差,換句話講,投資者只關心回報分佈中的前兩階矩(first two moments)。如果回報服從正態分佈,那麼投資者這麼做確實合理,但是,我們知道許多投資組合的回報並非服從正態分佈。事實上,許多投資組合的分佈具有偏態(skewness)以及超額峰度(excess kurtosis)特性。偏態與分佈的第三階矩有關,峰度與分佈的第四階矩有關。與正態分佈相比,具有正偏態的分佈會產生更多的高回報和更少的低迴報,具有負偏態的分佈會產生更多的低迴報和更少的高回報。超額峰度分佈產生高回報和低迴報的機會均多於正態分佈。許多投資者對出現極端負回報的可能性非常擔心,他們可能願意在具有負偏態或具有超額峰度的投資組合裡得到更高的預期回報。
(2)我們假設在式(1-3)中對應於不同投資的ε項為相互獨立,這等於是說投資回報的相關性完全取決於投資本身與市場組合的相關性,這一假設顯然不成立。福特和通用汽車同屬於汽車行業,兩家公司的股票會有一定的相關性,這一相關性並非來自它們與市場的相關性。以上討論說明對應於不同投資的ε項並非相互獨立。
(3)我們假設投資者只關心某一特定時段的投資回報,而且我們假設不同投資者所選定的時段均相同,這一假設顯然不成立。有些投資者(如養老基金)的投資期限很長,而有些投資者(如當日交易員(day trader))的投資期限很短。
(4)我們假設投資者可同時以相同的無風險利率借入或借出資金。在正常的市場條件下,對於信譽好的大型金融機構而言,以上假設近似成立;對於小投資者而言,這一假設不成立。
(5)我們在分析中不考慮稅收。我們知道,某些地區對資本收益(capital gain)的稅收處理不同於對股息和其他收入,而某些投資產品會有特殊的稅收優惠;還有,並非所有的投資者均會受同一稅率的制約。在實際中,投資者進行投資會將稅收考慮在內。對免稅的養老基金適用的投資可能並不適用於需要支付很高稅率的某紐約居民,這一說法反過來也成立。
(6)最後,我們假設所有投資者對任意給定的投資資產的預期回報、回報率的標準差的估算,以及對投資產品之間的相關係數的估算相同。換句話講,我們假設投資者具有一致性預期性(homogeneous expectations),這顯然不成立。事實上,正如以上討論所示,在一致性世界裡不會出現交易行為。
即使如此,資本資產定價模型已經被證明是管理人員進行投資組合管理的強有力的工具。關於股票的beta估計已經非常容易取得,同時由資本資產定價模型所計算出的投資期望值通常被管理人員用來當作檢驗投資好壞的標準,我們接下來將進一步解釋這一點。
1.3.2 alpha
當我們觀察市場回報為RM時,我們對一項beta值等於β的投資組合的預期為多少?資本資產定價模型將投資組合的預期回報與市場的預期回報聯繫在一起,同時模型也將投資組合的預期回報與市場的真實回報聯繫到一起
E(RP)=RF+β(RM-RF)
其中RF為無風險利率,RP為投資組合的回報。
【例1-2】 考慮一個beta為0.6的投資組合,無風險利率為4%。
當市場回報為20%時,投資組合的預期回報為
0.04+0.6×(0.2-0.04)=0.136
即13.6%;當市場回報為10%時,投資組合的預期回報為
0.04+0.6×(0.1-0.04)=0.076
即7.6%。當市場回報為-10%時,投資組合的預期回報為
0.04+0.6×(-0.1-0.04)=-0.044
即-4.4%。投資組合的預期回報與市場回報的關係如圖1-6所示。
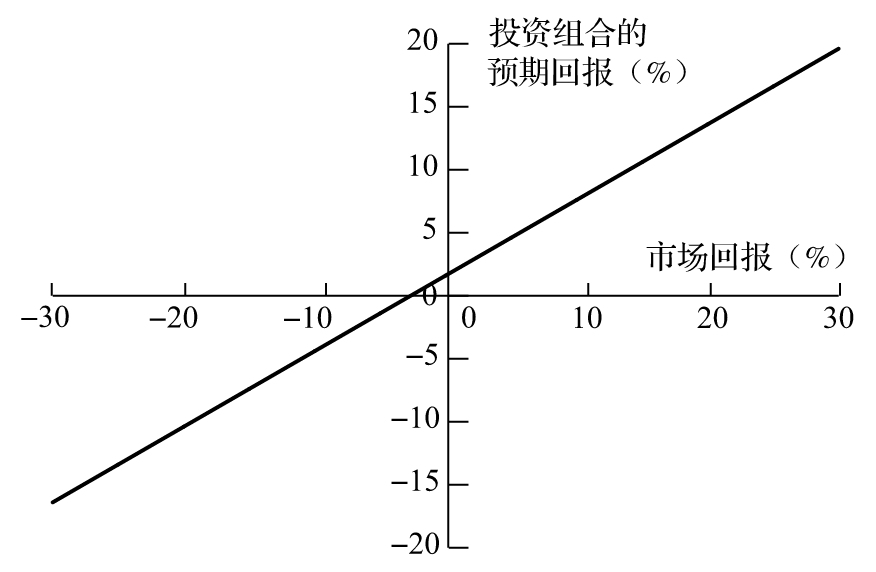
圖1-6 投資組合的預期回報與市場真實回報的關係(組合的beta為0.6,無風險利率為4%)
假定投資組合的真實回報大於預期回報,即
RP>RF+β(RM-RF)
我們可以說,對於一定數量的系統性風險而言,投資組合經理產生了更為突出的回報,而額外回報量為
α=RP-RF-β(RM-RF)
該額外回報通常被稱為是由投資組合經理產生的alpha。[1]
【例1-3】 某投資組合的beta為0.8,1年期無風險利率為5%,市場在1年內的回報為7%,投資組合經理的回報為9%,該經理產生的alpha為
α=0.09-0.05-0.8×(0.07-0.05)=0.024
即2.4%。
投資組合經理會不斷地努力來產生正的alpha,其中一種做法是尋找比市場表現更好的股票,另一種方法是市場擇時(market timing)。這一做法涉及對市場變化做出預測,當預計市場會上漲時,投資經理會將資金從保守的國債投資轉移到股票市場;當預計市場會下跌時,投資經理會將資金從股票市場轉移到保守的國債投資。在第4章中,我們解釋了對衝基金生成正的alpha的投資策略。
雖然資本資產定價模型採用了一些簡化的假設,但是由模型產生的alpha和beta參數被廣泛應用於描述投資的特性。beta描述了由於承擔系統性風險取得的回報,beta值越高,投資組合所承擔的系統性風險也越高,回報中有更多的成分取決於市場回報;alpha代表了投資組合管理得當(或者是因為運氣好)所帶來的額外回報。一個投資者取得正的alpha一定是建立在另一個投資者取得負的alpha的代價之上,所有投資者的alpha的加權平均為0。
[1] alpha也被稱作詹森阿爾法,因為它是由邁克爾·詹森(Michael Jensen)在衡量對衝基金表現時首先引入的,見第4.3節。