e1 John Hull 風險管理與金融機構 v5
1.2 有效邊界
在這裡我們引入第三種投資資產。這種資產可同前面的兩種資產進行任意組合,這樣做可以進一步產生不同的風險-回報組合,使我們 的投資回報率進一步往“西北”方向移動。在這之後我們又可以引入第四種資產,而這第四種資產又可以同前面3種資產進行不同的組合而產生新的投資機會,我們繼續 這一過程,當我們考慮了所有由圖1-1所顯示的風險投資資產以後,我們就可以構造出所謂的有效邊界(efficient frontier)。在圖1-3中,有效邊界是我們的回報曲線朝西北方向移動的極限。對應有效邊界的任意一點,我們不可能找到某種投資會比其更優化。這句話是 指我們不可能會找到某一資產投資回報比有效邊界的點所對應的投資回報更高,而同時所對應的標準差更低。圖1-3中有效邊界的東南方向代表所有不同的投資可能, 對應於有效邊界的“東南”(右下角)方向的任何一點A,我們都可以在有效邊界中找到一點並使其風險-回報替 換關係比所對應的點A的風險-回報替換關係更好。
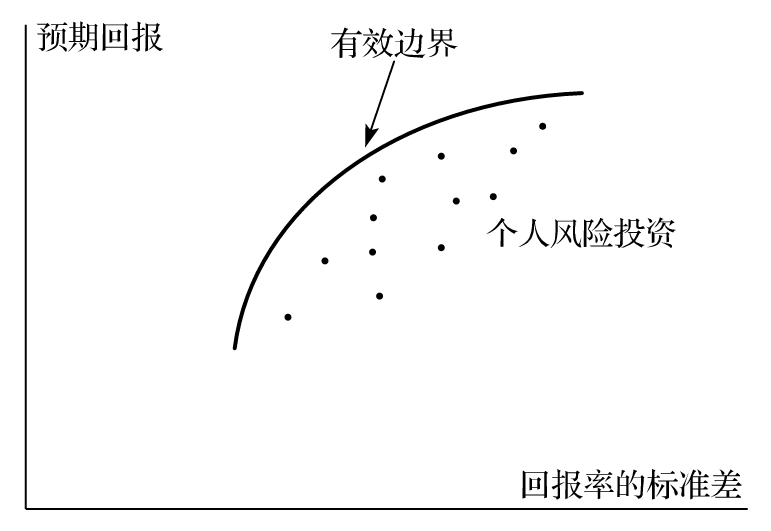
圖1-3 由具有不同風險的投資資產所產生的有效邊界
在圖1-3中我們只考慮了具有風險的投資。如果引入所有可能投資的話,那麼有效邊界又會變成什麼樣子呢?特別地,當我們引入無 風險投資時,會發生什麼情況呢?假定無風險投資所對應的回報率為RF, 在圖1-4中,我們用F點來代表無風險投資,從F點開始 我們引入同原有效邊界相切的一條直線,M代表切點。以下我們將要說明,直線FJ將 會是新的有效邊界。
如果將佔整體資金百分比βI(0<βI<1)的資金投入風險投資組合M, 然後將其他所有資金投放於無風險資產之中,這樣做會帶來什麼效果呢?如式(1-1)所示,我們進行這樣的組合之後,投資組合的預期回報E(RI)由下式給出
E(RI)= (1-βI)RF+βIE(RM)
由式(1-2)可知,我們得出投資組合回報率的標準差為βIσM[1],這裡σM代 表投資組合M的標準差。在圖1-4中,我們用I點來代表 以上表達式所闡明的風險-回報關係,從預期回報以及標準差兩方面來看,點I與F的 距離與點M與F的距離的比例為βI。
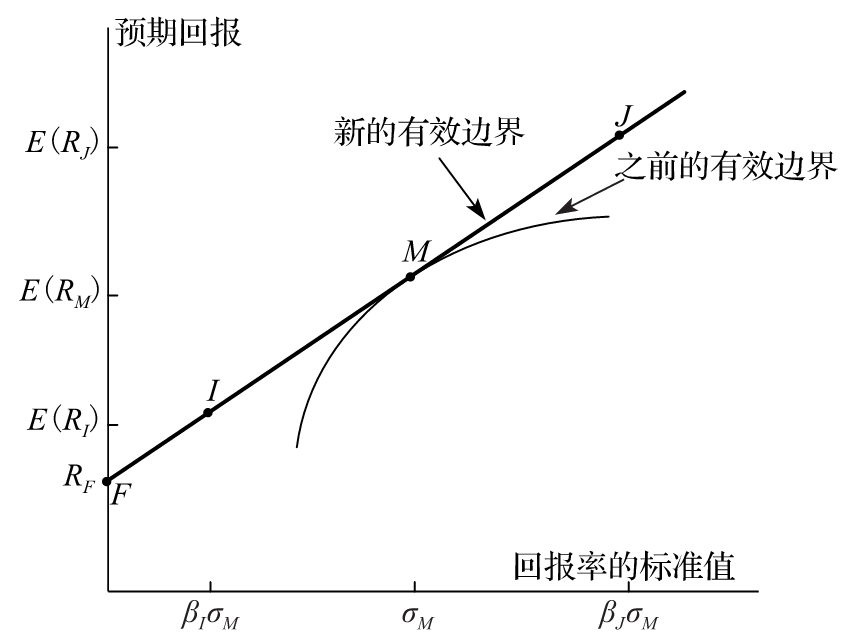
圖1-4 包含所有投資資產的有效邊界
注:I點所對應的投資由投入百分比為βI數量的資金在投資組合M中和1-βI數量的無風險資產所組成,J點 所對應的投資是以無風險利率借入的βJ-1數量 資金,然後將所有的資金(擁有的和借入的)全部投入投資組合M中所組成的。
直線FM上的所有點均可以由投放一定數量資金在M投 資組合以及一定數量資金在無風險資產F來取得,此直線上任意一點所對應的風險-回報關係要優於我們之前所討 論的有效邊界上的風險-回報關係,直線FM也因此成為新的有效邊界。
假定我們可以按利率RF借 入及借出資金,我們因此可以構造出從F點至M點以至於超 出M點的射線。假定我們的目的是構造出由圖中J點所表示 的組合投資,J點至F點距離是M點 至F點距離的βJ(βJ>1)倍。我們首先借入βJ-1數量的資產,然後將所有資產投入M點 投資組合之中。去掉應付利息之後,新的投資組合J所對應的預期回報為
E(RJ)=βJE(RM)-(βJ-1)RF=(1-βJ)RF+βJE(RM)
J點的標準差為βJσM。這樣我們清楚地展示了J點所對應的風 險-回報關係。
這裡的討論說明:當引入無風險投資後,有效邊界變成一條直線。換句話說,在由圖1-4所示的有效邊界上,預期回報與標準差之間 一定有一種線性的替換關係。所有的投資者都應選擇同樣的風險性資產,即M點所對應的投資組合,然後將風險性 資產與借入或借出的無風險資金進行不同比例的組合來體現他們的風險偏好。
現在要簡要說明一下投資組合M必須包含所有可能的風險投資資產。假設某個特 殊的投資資產沒有含於投資組合M之中,這樣就會造成沒有投資者持有這一資產,其價格會下跌,預期回報會增 加,最終成為組合的一部分。我們還可以進一步說明,為了保證每種投資資產的供需關係,每個風險投資資產的價格會得到調整,因此組合M中 的各個風險資產數量必須同整個經濟中所有可能投資資產成一定比例,這樣的投資組合M通常被稱為市場投資組合(market portfolio)。
[1] RF是無風險利率,為常數,E[RF]=RF,σF=0。 ——譯者注