e1 John Hull 風險管理與金融機構 v5
1.1 投資者的風險-回報關係
所有的基金經理都知道,投資時風險和回報之間有一個替換關係:風險越大,可能實現的回報越高。事實上這種替換關係介於風險和預 期回報之間,而並非風險與實際回報之間,“預期回報”一詞有時會使人產生誤解,在日常生活中“預期”一詞通常被理解為非常可能發生的事情,但統計學家卻將某一 變量的預期值定義為其平均值。因此預期回報是指對投資回報的加權平均,這裡的權重對應於這一投資回報所出現的各種可能的概率。可能的回報及相應的概率可以從歷 史數據中估計,或者通過主觀估計。
表1-1 將10萬美元資金投資於股票在1年後所得的回報
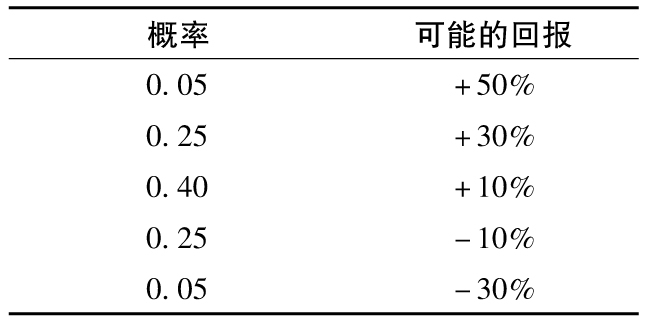
例如,假定你用10萬美元資金進行投資,投資期限為1年。一種可能是將所有資金投資於國債,其相應的年回報率為5%[1], 此項投資無風險,但預期回報率只有5%。另外一種可能是將所有資金投入某隻股票。為簡單起見,我們用表1-1來顯示該股票各種可能的回報以及相對應的概率。表 中回報率+50%所對應的概率為0.05,回報率+30%出現的概率為0.25,其他不同的回報率以及概率在表中均有顯示。將回報率記為小數點形式,股票的預 期回報率為
0.05×0.50+0.25×0.30+0.40×0.10+0.25×(-0.10)+0.05×(-0.30)=0.10
計算結果顯示,當你願意承擔一定的風險時,投資的預期回報率可以由投資國債的5%提高到10%。如果投資一切順利,你的回報也 可能達到+50%,但如果投資不順利,也可能是-30%,其相應損失為3萬美元。
馬科維茨(Markowitz,1952)是研究投資風險-回報替換關係的先驅之一,後來夏普(Sharpe,1964)及其 他人以馬科維茨理論為基礎,進一步發展了資本資產定價模型(capital asset pricing theory)。資本資產定價模型顯示了預期回報和系統性風險的關係。1976年,羅斯(Ross)發表了風險套利定價理論(arbitrage pricing theory),這一理論將資本資產定價理論中單一系統性風險假設延伸到多系統性風險。這些頗具洞察力的理論研究成果對投資組合管理人理解和分析風險-回報關係產生了巨大 影響,在下一節中我們將回顧這些重要理論。
1.1.1 風險量化
當你選定某一投資後,如何將所面臨的風險進行量化呢?一種便捷的方式是將風險量定義為年回報率的標準差,也就是
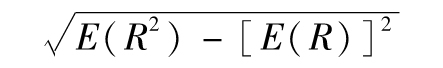
其中R指年回報率,E為 預期符號,E(R)代表年回報率的期望值。由表1-1可 知,我們可以算出E(R)為0.1。為了計算E(R2),我們必須以概率為權重對回報率的平方進行 加權平均:
E(R2)=0.05×0.502+0.25×0.302+0.40×0.102+0.25
×(-0.10)2+0.05×(-0.30)2=0.046
故年回報率的標準差為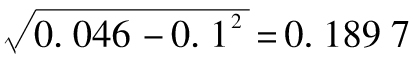 ,
即18.97%。
,
即18.97%。
1.1.2 投資機會
假定用期望值及標準差來描述完全不同的投資機會,我們可以用圖1-1來表示具有不同風險的投資可能,其中橫軸表示回報率的標準 差,縱軸表示預期回報。
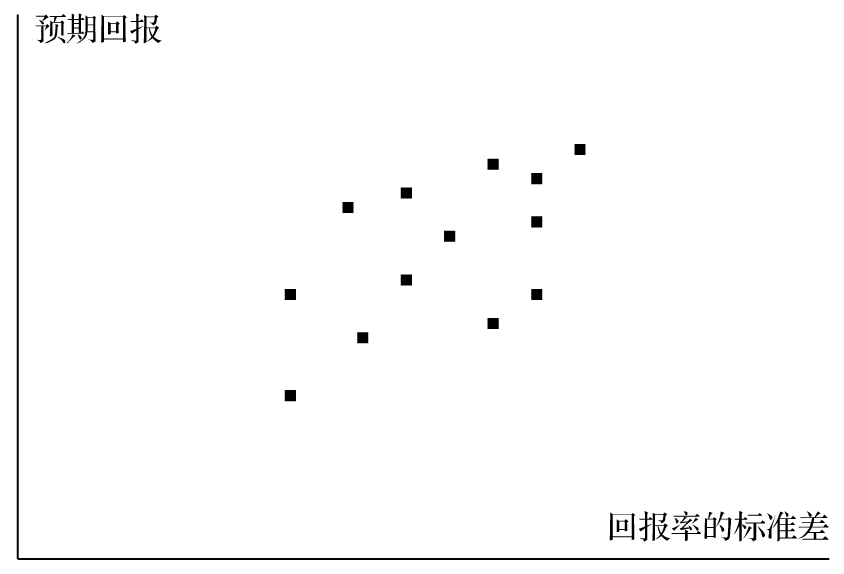
圖1-1 具有不同風險的投資資產
當得出某些投資回報率的標準差以及預期回報後,我們自然會想如果將這些投資進行不同的組合又會產生什麼效果呢?假設兩種投資資 產的回報率為R1和R2,如果我們按w1的 比例投入第一種資產,按w2=1-w1的比例投入第二種資產,這樣所產生的投資組合的回報率為
w1R1+w2R2
投資組合的預期回報為
μP=w1μ1+w2μ2
(1-1)
其中μ1為第一 種資產的預期回報,μ2為第二種資產的預期回 報。投資組合回報率的標準差為
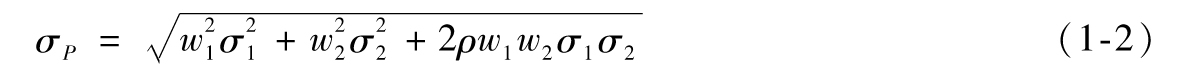
其中σ1與σ2分別為R1和R2的 標準差,ρ是R1和R2的相關係數。
假定μ1為 10%,σ1為16%,μ2為15%,σ2為 24%;R1和R2的相關係數為0.2。表1-2顯示出在不同比例投資下投資組合的預期回報以及回報率的標準差。以不同比 例投資於兩種資產會給投資者帶來範圍廣泛的回報組合,圖1-2是其圖形顯示。
表1-2 由兩種投資資產構成的投資組合的預期回報以及回報率的標準差
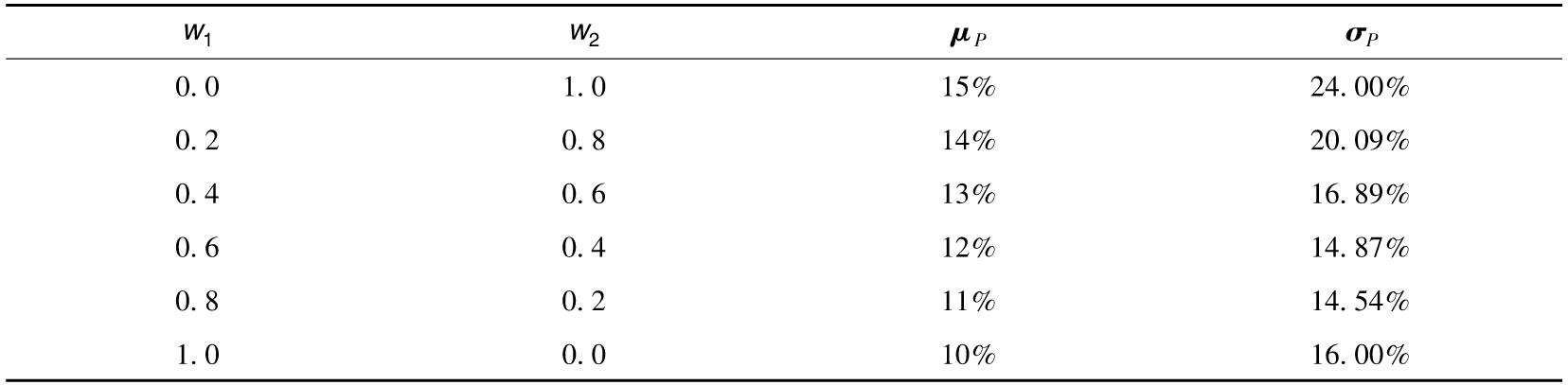
注:兩種資產的預期回報分別為10%及15%,回報率的標準差分別為16%及24%,兩種資產回報的相關係數為0.2。
大多數投資者都厭惡風險(risk-averse),他們希望在增加預期回報的同時也減少回報率的標準差,體現在圖1-1及圖 1-2中,他們希望自己的投資回報曲線朝“西北”(左上角)方向移動。從圖1-2中我們可以看到,對兩種投資進行不同的組合可以幫我們達到目的。例如,在第一 種資產中投入60%的資金,而在第二種資產中投入40%的資金,這樣做投資的預期回報率可以達到12%,其所對應的回報率的標準差為14.87%。這種組合比 只投資於第一種資產的效果要好(預期回報提高了2%,而回報率的標準差降低了1.13%)。
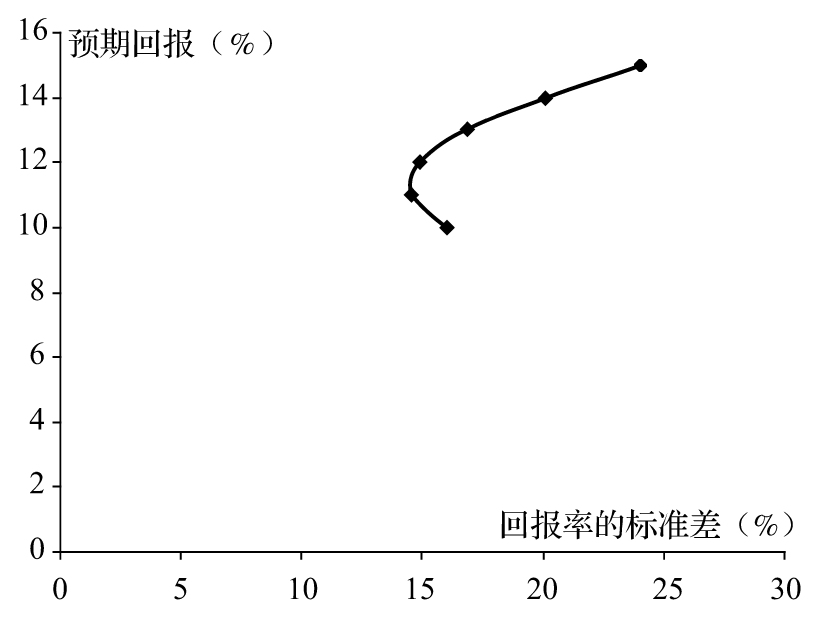
圖1-2 表1-2計算出的兩種資產構成的投資組合的不同的風險-回報
[1] 這一數值比較接近歷史平均值,但顯著高於2008年以來美國國債及其他一些國債的收益率。