e1 Stephen Ross 公司理財 v12A
24.3 進一步探討:布萊克-斯科爾斯期權定價模型
在本節中,我們將更深入地研究影響期權定價的因素和它們對期權價值的影響。表24-4總結了影響期權定價的因素以及它們對期權價值正向或負向的影響。在表中,加號表示影響因素對期權價值產生正向影響,反之為負向影響。
表24-4還指出,5種影響效果中的4種可以用希臘字母來表示,我們將在接下來的章節討論它們。在某些情況下,期權價值的計算可能相當複雜,但現在我們可以通過在網絡上廣泛使用的期權計算器來解決這個問題。
表24-4 影響美式期權(非派息股票)的5個因素
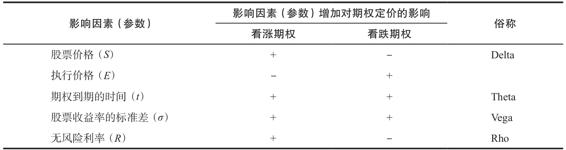
注:期權到期的時間越長,美式看跌期權價格越高,但對於歐式看跌期權而言,其價格可能更高也可能更低。
24.3.1 股票價格
股票價格對看漲期權和看跌期權價值的影響是十分明顯的。隨著股票價格的上升,看漲期權的價值增加,而看跌期權的價值減少。然而,股價對期權價值影響的強弱取決於期權的“貨幣性”(價外期權還是價內期權)。
在其他影響因素不變的情況下,我們將在圖24-1中闡述看漲和看跌期權價格與標的股價之間的關係。在圖中,橫軸表示股價,縱軸衡量期權價格。我們注意到,表示看漲和看跌期權價值的線是彎曲的,這是因為價外期權對標的股票的價格變動沒有價內期權那麼敏感。
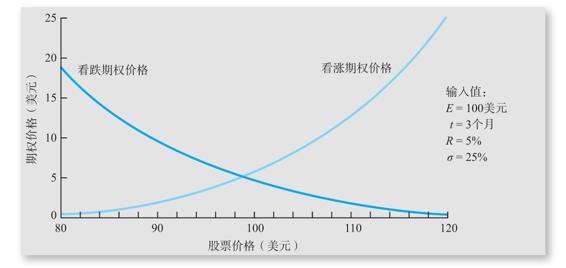
圖24-1 看跌期權和看漲期權定價
期權價值對標的股票價格變動的敏感性被稱為期權的delta值。對於歐式期權而言,我們可以直接測量delta值,如下所示:
看漲期權的delta=N(d1)
看跌期權的delta=N(d1)-1
用來計算delta的N(d1)和我們用來計算期權價值的N(d1)是一樣的,所以我們已經知道怎麼做了。N(d1)是一個概率,所以它的取值在0到1之間。
對於標的股票價值的微小變化,期權價值的變化近似於其delta值乘以股票價格的變化。
期權價值的變化≈Delta×股票價格的變化
為了說明這一點,假設以下條件:
S=120美元
E=100美元
R=8%/年,連續複利
σ=80%/年
t=6個月
使用布萊克-斯科爾斯的期權定價公式,看漲期權的價值為37.80美元。delta值[N(d1)]為0.75,這說明如果股票價格變動1美元,期權價值將同向變動0.75美元。
我們可以通過將股票價格變為121美元並重新計算期權價值來進行驗證。如果我們這樣做,這個看漲期權的新價值為38.55美元,比原來增加了0.75美元;因此,這個近似值是相當準確的(保留小數點後三位)。
如果我們以相同的輸入值對看跌期權定價,看跌期權的價值為13.88美元。delta值為0.75-1,即-0.25。如果我們將股票價格提高至121美元,該看跌期權新的價值為13.63美元,變動值為-0.25;因此,只要股票價格變化相對較小,這個近似是相當準確的。
回過頭來看圖24-1,我們現在可以看到為什麼隨著股票價格的上漲(對於看漲期權而言)和下跌(對於看跌期權而言),曲線會變得越來越陡峭。深度價內期權的delta值接近於1,而深度價外期權的delta值接近於0。
【例24-6】delta
假設有如下條件:
S=40美元
E=30美元
R=6%/年,連續複利
σ=90%/年
t=3個月
看漲期權的delta值是多少呢?看跌期權呢?哪一個對於股票價格的變化更為敏感?為什麼?
我們需要計算N(d1),你是否同意它是0.815,即看漲期權的delta值。看跌期權的delta值為0.815-1=-0.185,從絕對值來看比看漲期權要小得多,這是因為看漲期權是價內期權而看跌期權是價外期權。
24.3.2 期權到期的時間
對美式期權而言,期權到期的時間長度變化的影響也十分明顯。因為美式期權可以在到期前的任何時間行權,因此,延長期權的到期日不會有什麼壞處,同時有可能會帶來好處(尤其對於價外期權而言)。對於看漲期權和看跌期權而言,延長期權的到期日都會有積極的影響。
對於歐式看漲期權而言,延長期權的交割日也同樣不會產生消極影響。因為正如我們前面所討論的,未到期的期權的價值總是比到期的期權價值要大,延長期權的到期時間只會增加它的價值。對於歐式看跌期權而言,延長期權的到期時間可能會增加股權價值,也可能不會。正如我們已經討論過的,對於一個深度價內看跌期權,立即執行通常是理想的。所以此時延長期權的到期時間只會減少期權的價值。如果一個看跌期權是價外期權,延長期權的到期時間可能會增加它的價值。
圖24-2展示了增加看漲期權和看跌期權的到期時間對期權價值的影響。期權為平價期權。在圖中,一旦期權的到期時間達到6個月左右,期權到期時間的進一步增加對看跌期權的價值幾乎沒有影響。相反,看漲期權的價值一直在上升。
期權價值對時間流逝的敏感性稱為theta。有一個求theta值的公式,但是它相當複雜,因此我們這裡不提及。重要的是,我們需要意識到期權價值對時間的流逝是敏感的(特別是看漲期權)。要理解這為什麼很重要,想象一下你今天買了一個期權並持有1個月。在這個月裡,股票價格不會發生變化。你的期權價值將會發生什麼變化呢?
你的期權價值將會下降,這是因為到期日越來越接近,儘管標的資產的價格沒有發生變化。我們有時候說期權是一種消耗性資產,這意味著在其他因素保持不變的情況下,期權的價值隨著時間的推移而下降。隨著時間推移期權價值的下降趨勢被稱為時間損耗。期權的theta值是時間損耗速率的一種衡量。
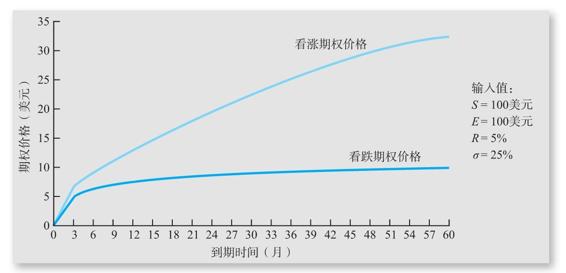
圖24-2 期權價格與到期時間
回顧我們之前學習的關於期權的章節,期權的內在價值為:
看漲期權的內在價值=Max[S-E,0]
看跌期權的內在價值=Max[E-S,0]
其中Max[S-E,0]代表取S-E和0之間較大的值。美式期權不會以低於它們內在價值的價格出售,因為如果這樣做,就會有套利機會。假設一隻股票賣60美元,執行價格為50美元的期限為3個月的看漲期權售價為8美元,你會怎麼想呢?
你會覺得自己將會變得富有,因為你可以以8美元買入期權,以50美元行權,然後以60美元賣出股票,這樣便可以獲得2美元的無風險利潤。為了防止這種類型的簡單套利,期權至少以其內在價值(即60-50=10美元)出售。實際上,期權可能以11美元出售。超過期權內在價值的額外的1美元被稱為時間溢價。換句話來說,期權的價值可表示為:
期權價值=期權內在價值+時間溢價
時間溢價隨著時間的推移而消耗或衰減。原因在於,在期權到期日那天,期權的價值正好就是它的內在價值:在那一天,期權被執行或發生違約。時間溢價的存在也解釋了我們之前觀察到的現象,即一個未到期的看漲期權總是比到期的期權更有價值。如果你到期行權,你就得到了內在價值。如果你賣掉它,你就得到了內在價值和剩餘的時間溢價。
【例24-7】時間溢價
2017年2月,特斯拉汽車的股價約為246.32美元。一個到期日為2017年11月、執行價格為250美元的看漲期權報價為27.28美元。一個相同執行價格的看跌期權報價為35.98美元。對於兩種期權,它們的內在價值和時間溢價是多少呢?
從看漲期權來看,我們知道它是價外期權,因為執行價格250美元高於股票價格246.32美元。它的內在價值為0,所以期權價值27.28美元就是時間溢價。而看跌期權是價內期權,它的內在價值為250-246.32=3.68美元。期權價值為35.98美元,所以時間溢價為35.98-3.68=32.30美元。
24.3.3 股票價格波動性
圖24-3說明了標的資產價格波動性的變化對期權價值的影響。如圖所示,對於看漲期權和看跌期權,股票價格波動性變化對期權價值產生的影響是正向且顯著的。事實上,增加標的資產價格波動性對它們的影響幾乎相同。
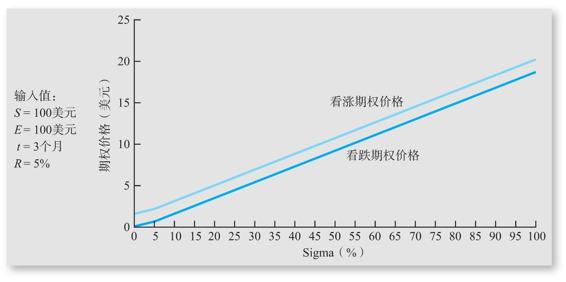
圖24-3 期權價格和Sigma值
期權價值對標的資產價格波動性的敏感性稱為vega值。[1]同樣,這個公式有點複雜,所以我們省略對它的展示。從圖24-3中可知,期權價值對標的資產價格的波動性非常敏感,標的資產收益率的標準差的變化會對期權價值產生強烈的影響。
24.3.4 無風險利率的變動
我們將在圖24-4中說明無風險利率的變化對期權價值的影響。如圖24-4所示,當無風險利率增加時,看漲期權的價值會增加,而看跌期權的價值會下降。注意,對於實際的利率變化,期權價值變化並不大。換句話來說,期權價值對利率變化不像對標的資產價格波動性變化那麼敏感。期權對利率變化的敏感性稱為rho值。
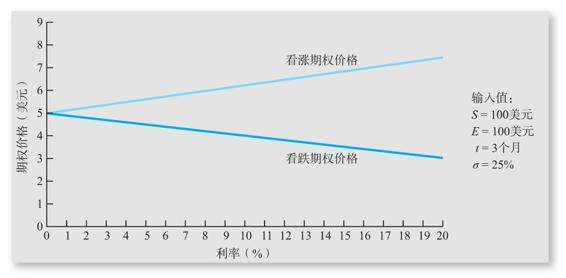
圖24-4 期權價格與利率
除了我們已經討論過的,還有一些其他的希臘字母,但我們將結束對它們的討論。我們接下來將討論布萊克-斯科爾斯期權定價模型一個非常重要的用法:用於計算隱含波動率。
24.3.5 隱含波動率
到目前為止,我們主要使用布萊克-斯科爾斯期權定價模型來計算期權價值,但它還有另一個非常重要的用途。在決定期權價值的5個因素中,4個因素可以直接觀察到:股票價格、執行價格、無風險利率和期權到期的時間,只有標的資產收益率的標準差是需要估計的。
我們在期權定價模型(OPM)中使用的標準差實際上是在期權期限內,預期的標的資產收益率的標準差。通常,我們已經知道期權價值,因為我們可以直接在金融市場中觀察到它。在這種情況下,我們可以使用期權價值,以及上述4個可直接觀察的輸入值,反推出標準差的值。當我們用這種方式得到標準差時,該標準差被稱為隱含標準差(implied standard deviation,ISD)(有人稱之為“iz-dee”),也被稱為隱含波動率。
為了說明上述計算,假設有以下條件:
S=12美元
E=8美元
R=5%/年,連續複利
t=6個月
同時,我們知道該看漲期權的報價為4.59美元。基於上述信息,未來3個月該期權的標的股票收益率的波動性將會有多大?
如果我們將所有的這些信息放到布萊克-斯科爾斯的模型中,僅剩下一個未知數:標準差(σ)。然而,直接把它求解出來是不可能的,因此必須要進行反覆試驗。換句話來說,我們開始嘗試對σ賦值,直到我們找到一個使該看漲期權價格為4.59美元的σ。
對於股票期權而言,0.50是一個適當的開始。如果你把這個值賦給σ,你會看到計算出來的看漲期權價值為4.38美元,低於4.59美元。回想一下,當σ增加時,期權的價值將會上升。所以接下來我們將嘗試將0.60賦給σ,得到的期權價值為4.53美元。再經過一些嘗試後,我們會發現該期權的隱含波動率為0.64,即64%。
如果你想要找到整個股票市場的ISD,你其實可以很容易做到。VIX是標準普爾500指數在未來30天的隱含波動率。它常被視為一個恐懼指標,因為VIX指數的上升表明在未來30天股票市場的波動性將增大。從歷史上看,VIX指數一直在15~20,儘管其在2008年市場動盪期間攀升至80。為了允許投資者利用波動性進行交易,場內交易(exchange-traded)的期貨和期權的VIX指數都可獲得。這裡有一個問題:假設你要計算VIX期權的ISD。這個數字意味著什麼?
【例24-8】ISD
2017年2月28日,社交網絡公司Facebook股票的收盤價為135.45美元。一個到期日是2017年9月15日、執行價格為140美元的看漲期權報價為8.25美元。到期日為2017年9月15日的美國國債收益率為1.077%。基於上述信息,Facebook股票收益率的預期波動性會有多大呢?
綜上所述,我們已有的相關數據為:
S=135.45美元
E=140美元
R=1.077%/年,連續複利
σ=?
t=199天
C=8.25美元
從這裡開始,將要嘗試對σ賦予不同的值以使期權的價值為8.25美元。正如你現在可能已經知道的那樣,使用期權計算器來求解σ會更容易。這就是我們所做的,求解出來的隱含標準差約為25%。
原則上,要求解出σ,我們需要將年利率1.077%轉換為連續複利。如果我們這樣做,將得到連續複利1.082 8%。但是我們會發現,期權價值對利率的微小變化並不敏感,在此情況下,這實際上並沒有什麼區別。基於此,在實踐中,連續複利問題常被忽略,尤其是當利率很低的時候。
概念問題
24.3a 什麼是期權的delta值、rho值,theta值和vega值?
24.3b 什麼是ISD?
[1] 希臘學者肯定知道“vega”不是希臘字母。(它是天琴座中的一顆恆星,也是雪佛蘭在20世紀六七十年代生產的一款特別容易被人遺忘的汽車。)