BUSINESS BOOKS

24.2　布萊克-斯科爾斯期權定價模型

我們接下來要討論的是布萊克-斯科爾斯期權定價模型。這一定價模型是一項重要發現，其發現者以此獲得了1997年諾貝爾經濟學獎。布萊克-斯科爾斯模型的建立非常複雜，因此我們只關注其主要結果以及如何使用它。

24.2.1　看漲期權定價

布萊克和斯科爾斯將股票無紅利分配條件下，歐式看漲期權的價值表示為C，該公式為：

C=S×N（d₁）-E×e^-Rt×N（d₂）　（24-5）

我們在前面定義過S、E和e^-Rt，N（d₁）和N（d₂）由計算得出。具體來看，N（d₁）是標準正態分佈隨機變量小於或等於d₁的累積概率，N（d₂）是標準正態分佈隨機變量小於或等於d₂的累積概率。概率的值可以通過表24-3來查找。

表24-3　累積正態分佈

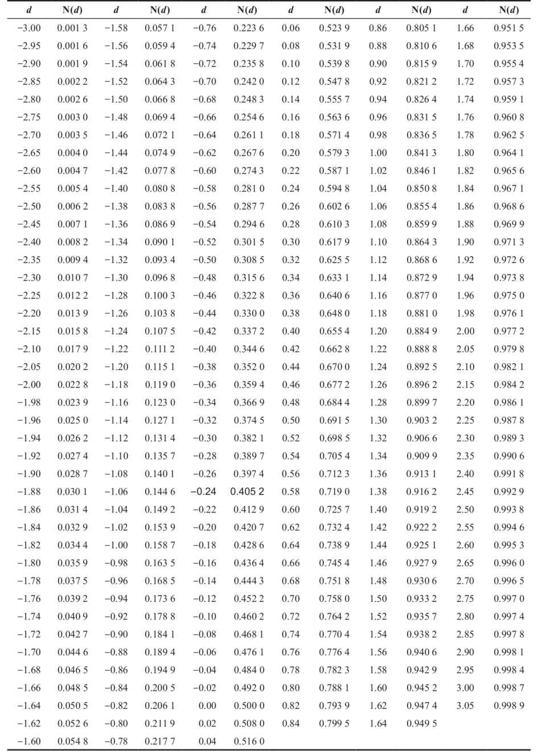
注：這個表格是觀測值小於等於d的值的概率[N（d）]。例如，如表所示，如果d是-0.24，那麼N（d）是0.405 2。

我們用一個例子來說明這個公式。

S=100美元

E=90美元

R=4%/年，連續複利

d₁=0.60

d₂=0.30

t=9個月

基於這些信息，看漲期權的價值C為多少？

我們需要先確定N（d₁）和N（d₂），通過查表24-3，得到N（d₁）為0.725 7，N（d₂）為0.617 9，由布萊克-斯科爾斯期權定價模型，計算得出看漲期權的價值為：

C=S×N（d₁）-E×e^-Rt×N（d₂）

=100×0.725 7-90×e^-0.04×0.75×0.617 9

=18.60（美元）

如本例所示，如果我們知道d₁和d₂（以及表）的值，那麼使用布萊克-斯科爾斯模型並不困難。但通常，我們需要計算d₁和d₂的值，布萊克-斯科爾斯模型中d₁和d₂的計算公式為：

d₁=[ln（S/E）+（R+σ²/2）×t]/（σ×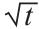）　（24-6）

d₂=d₁-σ×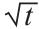

在這些表達式中，σ是標的資產收益的標準差。另外，ln（S/E）是當前股票價格除以執行價格的自然對數。

假設我們有以下信息：

S=70美元

E=80美元

R=4%/年，連續複利

σ=60%/年

t=3個月

基於這些數，可得d：

d₁=[ln（S/E）+（R+σ²/2）×t]/（σ×）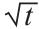

=[ln（70/80）+（0.04+0.6²/2）×0.25]/（0.6×）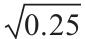

=-0.26

d₂=d₁-σ×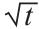=-0.26-0.6×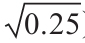=-0.56

查表24-3，得到N（d₁）和N（d₂）的值分別為0.397 4和0.287 7，代入數據，得到：

C=S×N（d₁）-E×e^-Rt×N（d₂）=70×0.397 4-80×e^-0.04×0.25×0.287 7=5.03（美元）

通過布萊克-斯科爾斯公式和我們的例子，你會發現看漲期權的價格取決於5個因素，這5個因素和我們前面定義的一致：現行股價，執行價格，期權到期的時間，無風險利率，股票收益的標準差。

【例24-5】看漲期權定價

假設給定以下信息：

S=40美元

E=36美元

R=4%/年，連續複利

σ=70%/年

t=3個月

股票看漲期權的價格是多少？

我們使用布萊克-斯科爾斯期權定價模型，首先計算d₁和d₂

d₁=[ln（S/E）+（R+σ²/2）×t]/（σ×）

=[ln（40/36）+（0.04+0.7²/2）×0.25]/（0.7×）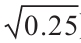

=0.50

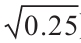d₂=d₁-σ×=0.50-0.7×=0.15

查表24-3得N（d₁）和N（d₂）的值分別為0.691 5和0.559 7，代入全部數據，得到：

C=S×N（d₁）-E×e^-Rt×N（d₂）=40×0.691 5-36×e^-0.04×0.25×0.559 7=7.71（美元）

關於概率N（d₁）和N（d₂）有一個問題。它們的概率指的是什麼？換言之，我們該如何解釋它們？答案是它們與現實世界中的任何事物都不對應。我們提到這一點，是因為對N（d₂）有一個常見的誤解。N（d₂）經常被認為是股票價格超過到期日執行價格的概率，也就是看漲期權是價內期權的概率。然而，這是錯誤的，除非股票的預期收益等於無風險利率。

24.2.2　看跌期權定價

到目前為止，我們的例子只集中在看漲期權上，而對看跌期權定價還需要進行一點額外的工作。首先，我們將看跌期權看作看漲期權，用布萊克-斯科爾斯模型為其估值。然後，我們用買賣平價關係來解決看跌期權的定價問題。舉例來說明，假設有以下信息：

S=40美元

E=40美元

R=4%/年，連續複利

σ=80%/年

t=4個月

股票看跌期權的價格是多少？

作為練習，請計算布萊克-斯科爾斯看漲期權的價格，看看你得到的看漲期權的價格是不是約為7.53美元。現在，我們回到買賣平價理論：

S+P=E×e^-Rt+C

通過買賣平價的公式來計算看跌期權的價格：

P=E×e^-Rt+C-S

代入相關數據，得到：

P=40×e^{-0.04×（1/3）}+7.53-40=7.00（美元）

此看跌期權的價值為7.00美元。因此，我們只要知道如何對看漲期權估值，就知道如何對看跌期權估值。

24.2.3　提示

我們來考慮另一看跌期權的定價，假設我們有以下信息：

S=70美元

E=90美元

R=8%/年，連續複利

σ=20%/年

t=12個月

股票看跌期權的價值是多少？

計算得到看漲期權的價值為1.65美元，回到買賣平價公式：

P=E×e^-Rt+C-S

代入數據，得到看跌期權價值：

P=90×e^-0.08×1+1.65-70=14.73（美元）

我們的看跌期權價值是不是有些奇怪？是的，因為股票價格是70美元，執行價格是90美元，你可以通過立即行使看跌期權獲得20美元，所以看起來我們有套利機會。然而事實並非如此。這個例子告訴我們，必須注意假設。布萊克-斯科爾斯模型適用於歐式期權（歐式期權只能在最後一天行使，而美式期權可以隨時行使）。我們的買賣平價理論僅適用於歐式期權。

我們的例子表明了美式看跌期權比歐式看跌期權更有價值。原因不難理解，假設你以80美元的執行價格買入看跌期權，最好的情況就是股價下跌到零。如果股票價格降到零，你的期權就不可能有更多的收益了，所以你會立即行使，而不是等待。如果是美式期權，你可以立即行使它，歐式期權則不能。一般來講，一旦看跌期權成為價內期權，行使期權就是值得的，因為額外的潛在收益是有限的，因此行使美式期權具有價值。

看漲期權會是怎樣呢？只要我們堅持持有非派息股票，儘早行使看漲期權就永遠不會是最佳選擇。原因並不複雜，賣出期權總比行使期權更有價值。換言之，看漲期權的價值與期權的類型沒有關係。

從數學的角度來看，我們現在面臨著一項挑戰。那就是，我們有了歐式看跌期權的公式，但到目前為止，還沒有美式看跌期權的公式。我們能夠對看跌期權進行估值，但沒有明確的計算公式。

概念問題

24.2a　決定期權價值的因素是哪5個？

24.2b　美式看跌期權和歐式看跌期權哪個價值更高？為什麼？