e1 Stephen Ross 公司理財 v12A
24.1 買賣平價理論
在前面討論過,看漲期權的持有者有在特定時期以某一固定價格購進一種資產的權利(而非義務),看跌期權的持有者有在特定時期以某一固定價格出售一種資產的權利。這一固定價格被稱為執行價格。
24.1.1 保護性看跌期權
讓我們來考慮以下投資策略,今天,你以110美元的價格買入1股微軟公司的股票。同時,你買入1份執行價格為105美元的看跌期權。這份看跌期權1年後到期,期權價格為5美元。你的總投資額為115美元,你計劃持有這份投資並在1年後將其出售。[1]
我們創建了表24-1,它展示了1年後不同股票價格的收益和損失。從表中我們可以看到,最壞的情況是你的投資價值下降到105美元。原因是,如果微軟的股價從現在起1年內低於105美元,你將行使看跌期權,以105美元的執行價格出售股票,因此這是最低迴報。
表24-1 1年後的收益和損失(原始投資:以110美元/股的價格購買1股股票,加上1份價值為5美元、執行價格為105美元的1年期看跌期權,總成本是115美元)
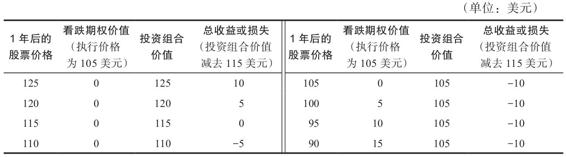
通過購買這份看跌期權,下行風險被降低為最多損失10(=115-105)美元。購買標的股票的同時購買看跌期權的策略被稱為保護性看跌期權(protective put)策略,它使你免遭某一特定值之上的損失,如同為股票買了一項保險。
在我們的例子中,我們選取了105美元的執行價格,你可以選擇更高的執行價格來進一步降低下行風險。當然,更高的執行價格意味著更高的看跌期權價格。因此,需要權衡降低風險的成本與報酬。
24.1.2 另一種策略
讓我們考慮一種不同的策略,你擁有115美元,購買了1份期權價格為15美元,1年期,執行價格為105美元的微軟公司看漲期權,並用剩下的100美元投資一項無風險的資產,例如國債。無風險利率為5%。
表24-2展示了這一策略。你的100美元將增長為105美元。比較表24-1與表24-2,你會發現無論標的股票的價格在1年內如何變動,投資者都能從兩種策略中獲得相同的收益。
兩種策略價值相同的事實解釋了為什麼這兩種策略的成本相同。如果其中一個策略的成本低於另一個策略,那麼就會出現套利機會,投資者會選擇低成本,而放棄高成本的策略。
表24-2 1年後的收益和損失(原始投資:一份價值為15美元、執行價格為105美元的1年期看漲期權,加上無風險利率為5%、價值100美元的無風險資產,總成本是115美元)(單位:美元)
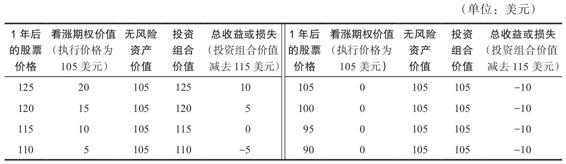
24.1.3 結論
我們的例子說明了一個重要的定價關係,即保護性看跌期權策略可以通過看漲期權(與看跌期權具有相同的執行價格)和無風險投資的組合完全複製。要注意的是,投資無風險資產的100美元與按無風險利率計算的期權執行價格的現值完全相同:105/1.05=100美元。
這就是買賣平價理論(put-call parity,PCP),如下所示:
標的股票價格+看跌期權價格=執行價格的現值+看漲期權價格 (24-1)
我們可以寫為:
S+P=PV(E)+C (24-2)
S和P分別是標的股票和看跌期權的價格,PV(E)和C分別是執行價格的現值和看漲期權價格。
由於執行價格的現值是用無風險利率計算的,因此可以將其視為面值等於執行價格的無風險純貼現工具(如國債)的價格。記住買賣平價理論最簡單的方法是記住“股票加看跌期權等於國債加看漲期權”。
買賣平價是一個代數表達式,這意味著它可以重新排列。假設我們知道每月的無風險利率為0.5%。執行價格為40美元的看漲期權售價為4美元,相同執行價格的看跌期權售價為3美元。兩者都有3個月的到期期限。標的股票價格是多少?
我們用買賣平價理論來求解這一問題:
S=PV(E)+C-P (24-3)
=40/1.0053+4-3=40.41(美元)
買賣平價理論給出了無風險資產(如國債)、看漲期權、看跌期權和股價之間的關係,已知其他3種資產的價格時,我們能算出第4種資產的價格。
【例24-1】買賣平價1
假設有一股票市場價格為60美元。一個執行價格為70美元半年期的看漲期權的市場價格為2美元。無風險利率是每月0.4%。執行價格為70美元半年期的看跌期權的價格是多少?
用買賣平價理論,我們得到:
P=PV(E)+C-S=70/1.0046+2-60=10.34(美元)
注意到,本例中看跌期權的價格遠高於看漲期權的價格,這是為什麼?
【例24-2】買賣平價2
假設股票的市場價格是110美元。1年期的平價看漲期權市場價格是15美元。到期日相同的平價看跌期權市場價格為5美元。你能結合這3種工具來構建一種無風險的投資嗎?怎樣做?無風險利率是多少?
這裡,我們用買賣平價理論來求解執行價格的現值
PV(E)=S+P-C=110+5-15=100(美元)
執行價格的現值為100美元。注意,因為期權是平價的,執行價格與股票價格都為110美元。所以,如果你今天把100美元投入無風險投資,1年後將得到110美元,那麼隱含的無風險利率顯然是10%。
24.1.4 連續複利:複習
回到第6章,我們看到投資的有效年利率(EAR)取決於計息頻率。在極端情況下,複利可以發生在每一時刻,或連續發生。假設你以每年6%的利率投資100美元,並連續複利。一年後你會得到多少錢?兩年後呢?
在第6章中,我們看到連續複利有效年利率為:
EAR=eq-1
其中q是利率(本例中為6%或0.06),e是數字2.718 28…,自然對數的底數。代入數據,我們得到:
EAR=eq-1=2.718 280.06-1=0.061 84
約等於6.2%。注意,大多數計算器都有一個標記為“ex”的鍵,因此執行此計算需要輸入0.06然後按此鍵。有效年利率為6.184%時,你的100美元投資將在1年後增長到106.18美元。2年後,它將增長為:
FV=100×1.061 842=100×1.127 5=112.75(美元)
在我們對期權進行估值時,出現連續複利的情況相當多。在本例中,我們首先將連續複利率轉化為有效年利率,再進行計算。其實我們可以不需要轉化,直接計算現值和未來值。每期利率為R,則t期後1美元初始投資的終值為:
FV=1×eRt
回到剛才的問題,以6%的連續複利率計算,100美元2年後的終值為:
FV=100×e0.06×2=100×2.718 280.12=100×1.127 5=112.75(美元)
和之前的計算結果一致。
同樣,我們可以計算利率為R,t期後1美元的現值:
PV=1×e-Rt
如果利率為8%,5年後15 000美元的現值為:
PV=15 000×e-0.08×5=15 000×2.718 28-0.4=15 000×0.670 32=10 054.80(美元)
【例24-3】連續複利
如果6個月後將收到500美元,按每年9%的利率連續計息,這筆錢的現值為多少?
這種情況下,注意週期數等於一半,因為6個月是半年。現值為
PV=500×e-0.09×0.5=500×2.718 28-0.045=500×0.956=478(美元)
回到買賣平價理論,我們可以將其寫為:
S+P=PV(E)+C
如果我們假設R是年連續複利的無風險利率,那麼我們可以將其寫為:
S+P=E×e-Rt+C (24-4)
其中t是期權的到期時間(以年計)。
最後,假設我們得到一個有效年利率,我們需要將它轉換為連續複利率。如果實際無風險年利率為8%,那麼連續複利的無風險利率是多少?
回到我們的公式:
EAR=eq-1
代入數據,得到:
0.08=eq-1
eq=1.08
ln(eq)=ln1.08
q=0.076 96
約為7.7%。注意,大多數計算器都有一個標記為“ln”的按鈕,因此執行此計算需要輸入1.08,然後按此鍵。
【例24-4】買賣平價3
假設一隻股票市場價格為30美元,一個執行價格為25美元,3個月的看漲期權市場價格為7美元,執行價格相同的3個月看跌期權市場價格為1美元,那麼連續複利的無風險利率為多少?
我們需要將相關數據代入買賣平價關係中:
S+P=E×e-Rt+C
30+1=25×e-R×0.25+7
24=25×e-R×0.25
0.96=e-R×0.25
ln0.96=lne-R×0.25
-0.040 8=-R×0.25
R=0.163 3或16.33%
約為16.33%,這是一個非常高的無風險利率!
概念問題
24.1a 什麼是保護性看跌期權策略?
24.1b 什麼是保護性看跌期權策略的替代策略?
[1] 當然,在現實中,你不能購買1股期權,所以你需要購買100股微軟股票和1份看跌期權合約(至少)才能真正實施這一策略。我們是按每股計算來解釋的。