BUSINESS BOOKS

附錄19A　確定目標現金餘額

根據前一章關於流動資產的綜合討論，目標現金餘額（target cash balance）涉及持有太多現金的機會成本（持有成本）和持有太少現金的成本（短缺成本，也叫調整成本（adjust-ment cost））之間的權衡。這些成本的性質取決於公司的營運資本政策。

如果公司採用彈性的營運資本政策，它可能會持有一個有價證券投資組合。在這種情況下，調整成本，或者說短缺成本，就是買入和賣出證券的相關交易成本。如果公司採取限制性的營運資本政策，它可能靠借入短期借款來彌補現金短缺。這種情況下的成本就是利息與安排借款產生的其他相關開支。

在下面的討論中，我們假設公司採取彈性政策。那麼，它的現金管理就包括在有價證券上的現金出入。這是關於該主題的一種傳統方法，也是解釋持有現金的成本和利益的好方法。

然而，請記住，現金和貨幣市場投資之間的差異正在變得越來越模糊。例如，我們如何對可開支票的貨幣市場資金進行分類呢？這種近似現金變得越來越常見了。它們沒有普及的主要原因可能是法規限制了它們的使用。我們將在下面的討論中多次回到這個主題。

19A.1　基本理念

圖19A-1列示了彈性公司的現金管理問題。如果公司試圖保持很低的現金持有量，它將發現自己用光現金的情況會比理想中的更頻繁，因此會比當現金餘額較高時更頻繁地出售有價證券（並且之後或許還要再購買有價證券來取代那些被出售的）。因此，在現金餘額較低的情況下，交易成本很高。隨著現金餘額的增加，這些成本會降低。

相反，如果公司持有少量現金，那麼持有現金的機會成本就會很低。隨著現金持有量上升，機會成本增加，因為公司放棄了越來越多本來可以賺取的利息。

在圖19A-1中，成本之和用總成本曲線給出。如圖所示，當兩條個別成本曲線相交在C*點時，總成本最小。在這個點上，機會成本和交易成本相等。這個點就是目標現金餘額，是公司應該設法找到的點。

圖19A-1和第18章的圖18-2實質上是相同的。然而，正如我們後面討論的，現在我們可以更多地討論在現金上的最優投資和影響它的因素。

19A.2　BAT模型

BAT（Baumol-Allais-Tobin）模型是分析現金管理問題的一個經典方法。我們將說明如何應用這個模型來實際建立目標現金餘額。這是一個有助於說明現金管理以及流動資產管理因素的直觀模型。

為了推導BAT模型，假設Golden Socks公司在第0周（即一開始）有現金餘額C=120萬美元。每一週，現金流出比現金流入多60萬美元。結果，在第2周結束時，現金餘額將降至0。這兩週的平均現金餘額為期初餘額（120萬美元）加期末餘額（0），再除以2，即（120萬美元+0）/2=60萬美元。在第2周結束時，Golden Socks通過存入另一筆120萬美元來補充現金。

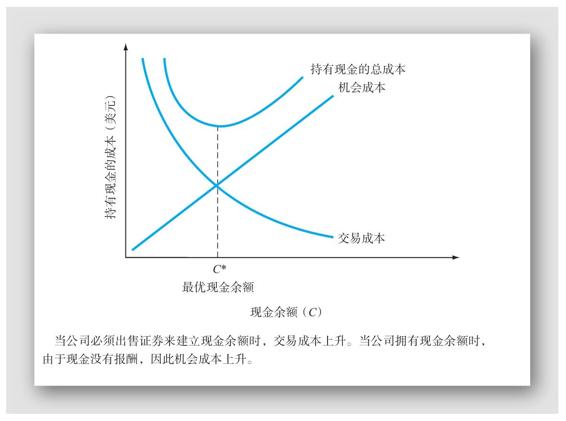
圖19A-1　持有現金的成本

就像我們所講述的那樣，Golden Socks簡單的現金管理策略可以歸結為每兩週存入120萬美元。圖19A-2展示了這種政策。請注意現金餘額是如何在每週下降60萬美元的。因為公司在賬戶中追加了120萬美元，在每個長達兩週的期間結束時，餘額會達到0。結果列示為圖19A-2中的鋸齒圖形。

我們隱含地假設每天的淨現金流出是相同的，而且是可以明確得知的。這兩個假設使得模型變得容易處理。我們將在下個部分講述如果這兩個假設不成立，應該怎麼處理。

如果C設定的更高一些，比如說240萬美元，現金可以維持4周，直到公司必須出售有價證券為止；但是公司的平均現金餘額將從60萬美元增加到120萬美元。如果C設定為60萬美元，現金就會在1周用完，公司將不得不更頻繁地補充現金，而平均現金餘額將從60萬美元減少到30萬美元。

每當補充現金時，都會發生交易成本（例如，出售有價證券的佣金），因此建立較大的期初餘額可以降低與現金管理有關的交易成本。然而，平均現金餘額越大，機會成本（本可以從有價證券上賺取的報酬）越高。

為了確定最優策略，Golden Socks需要了解以下3件事情：

F為進行一次證券交易以補充現金的固定成本；

T為在相關計劃期間，比如1年，為滿足交易目的所需的現金總額；

R為持有現金的機會成本，即有價證券的利率。

有了這些信息，Golden Socks公司就可以確定在任何特定的現金餘額政策下的總成本，進而可以確定最優的現金餘額政策。

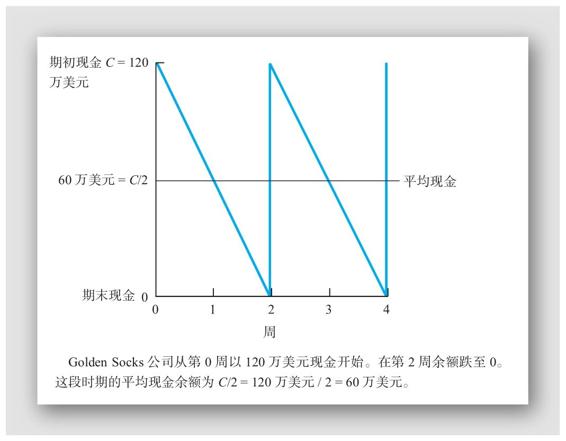
圖19A-2　Golden Socks公司的現金餘額

1.機會成本

為了確定持有現金的機會成本，我們必須求出所放棄的利息是多少。Golden Socks公司平均持有C/2的現金。這些現金可以賺取利率為R的利息。因此現金餘額的機會成本就等於平均現金餘額乘以利率

機會成本=（C/2）×R　（19A-1）

例如，假設利率為10%，不同備選方案的機會成本如下表所示。

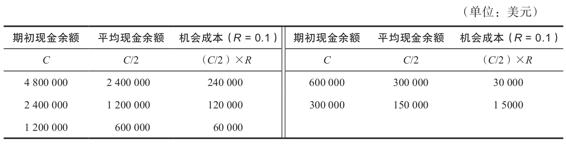
在原來的情況下，期初現金餘額為120萬美元，平均餘額為60萬美元。Golden Socks公司可以用它（在10%的利率下）賺取6萬美元的利息，因此這就是公司在這個策略下放棄的金額。請注意，機會成本隨著期初（和平均）現金餘額的增加而增加。

2.交易成本

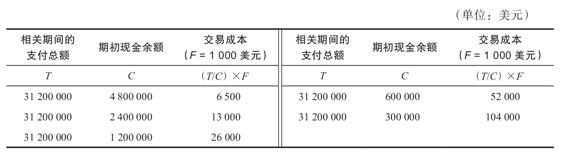
為了確定一年的總交易成本，我們需要知道Golden Socks公司在一年中必須出售多少次有價證券。首先，由於每週支出現金60萬美元，因此這一年的現金支付總額是T=60萬美元×52周=3 120萬美元。如果期初現金餘額設定為C=120萬美元，Golden Socks公司每年要出售120萬美元的證券的次數為：T/C=3 120萬美元/120萬美元=26次。每次的成本為F，因此交易成本為

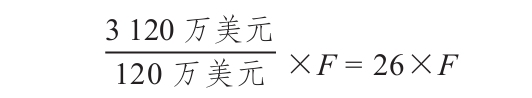
大致來說，總交易成本就是

交易成本=（T/C）×F　（19A-2）

在這個例子中，如果F是1 000美元（一個不太真實的大額數字），交易成本將是26 000美元。

我們計算了一些不同策略下的交易成本，如下表所示：

3.總成本

既然我們有了機會成本和交易成本，我們就可以把它們相加來計算總成本

總成本=機會成本+交易成本=（C/2）×R+（T/C）×F　（19A-3）

利用之前算出的數字，我們得到下表：

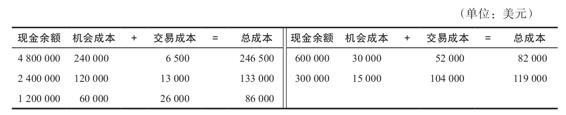
請注意，一開始時總成本接近250 000美元，在下降到82 000美元后，又開始上升。

4.解答

從上表中我們可以看出，現金餘額為60萬美元時，所導致的總成本最低：82 000美元。但當它為70萬美元或50萬美元或者其他可能的值時，結果會怎樣呢？最優餘額看起來介於30萬美元和120萬美元之間。記住這一點，我們就能很容易地採用試錯法求出最優餘額。然而，要直接求出答案也不難，接下來我們就這麼做。

回顧一下圖19A-1。如圖所示，最優現金餘額C*出現在兩條線的交點處。在這一點上，機會成本正好等於交易成本，因此在C*，我們有

機會成本=交易成本

（C*/2）×R=（T/C*）×F

稍微整理一下，可以寫成

C*2=（2T×F）/R

為了求出C*，對等式兩邊求平方根，得到

這就是最優期初現金餘額。

對於Golden Socks公司而言，我們已知T=3 120萬美元，F=1 000美元，R=10%。我們現在可以計算最優現金餘額為

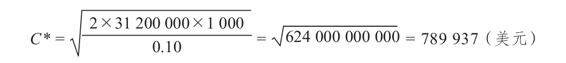
我們可以計算比這個現金餘額略高和略低的幾個餘額的不同成本，來驗證這個答案。

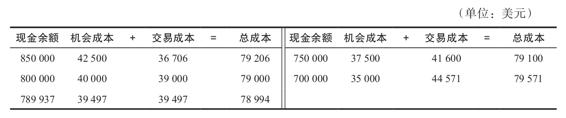
最優現金水平下的總成本是78 994美元，不管往哪個方向變動，總成本顯然會增加。

【例19A-1】BAT模型

Vulcan公司在一星期的7天中每天的現金流出是100美元。利率是5%，補充現金餘額的固定成本是每筆交易10美元。最優期初現金餘額是多少？總成本是多少？

本年中365天需要的總現金為365天×100美元=36 500美元。根據BAT模型，最優期初現金餘額是

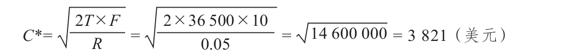
平均現金餘額為3 821美元/2=1 911美元，因此，機會成本為1 911美元×0.05=96美元。由於Vulcan每天需要100美元，因此3 821美元的餘額可以維持3 821美元/100美元=38.21天。公司每年必須補充這個賬戶365天/38.21天=9.6次，因此交易（指令處理）成本是96美元。總成本為192美元。

5.結論

BAT模型可能是確定最優現金頭寸的最簡單、最直觀的方法。它的主要缺點是假設現金流穩定而且確定。下面我們將討論一個應對這種侷限性的更復雜的模型。

19A.3　米勒–奧爾模型：一個更一般的方法

我們現在描述一個專門用來處理隨機波動的每日現金流入和流出的現金管理系統，即米勒–奧爾模型（Miller-Orr model）。在這個模型下，我們再次關注現金餘額。但是與BAT模型相反，我們假設餘額隨機上下波動，且平均變動為0。

1.基本理念

圖19A-3顯示了這個系統如何運作。它利用現金金額的上限和（U*）和下限（L）以及目標現金餘額（C*）來進行。公司允許它的現金餘額在上限和下限之間隨機變動。只要現金餘額處於U*和L之間，就不會發生任何事情。

當現金餘額達到上限（U*）時，就像在X點，公司從賬戶轉出U*-C*美元投到有價證券上。這個舉動使得現金餘額降到C*。同樣，如果現金餘額跌至下限（L），例如在Y點上，公司就會出售價值C*-L的有價證券，並將現金存入賬戶中。這個舉動使現金餘額升至C*。

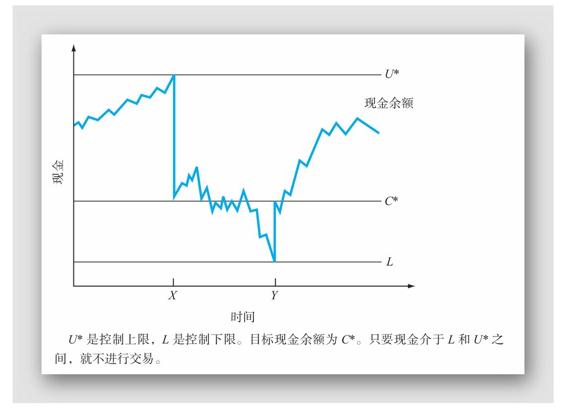
圖19A-3　米勒–奧爾模型

2.利用模型

剛開始，管理層設置下限（L）。這個界限實質上就是一個安全存量；因此它設定在哪兒取決於公司願意承受多大的現金短缺的風險，或者，最小值可能正好等於必需的補償性餘額。

與BAT模型一樣，最優現金餘額取決於交易成本和機會成本。同樣，每筆買賣有價證券的交易成本為F，假設是固定的。而且，持有現金的機會成本為R，即有價證券每一期的利率。

唯一需要知道的額外信息是σ²，即每期的淨現金流量的方差。此處的期間可以是任何時間長度，例如1天或者1周，只要利率和方差是基於相同的時間長度即可。

給定公司設定的L，米勒和奧爾證明，使持有現金的總成本最小化的目標現金餘額C*和上限U*，分別是^[1]

C*=L+（3/4×F×σ²/R）^（1/3）　（19A-5）

U*=3×C*-2×L　（19A-6）

進而，米勒–奧爾模型的平均現金餘額為

平均現金餘額=（4×C*-L）/3　（19A-7）

這些表達式的推導相當複雜，所以我們不在這裡給出。幸運的是，正如我們接下來展示的，結果並不難應用。

例如，假設F=10美元，月利率為1%，每月淨現金流量的標準差是200美元。每月淨現金流量的方差為

σ²=2002=40 000（美元）

我們假設現金餘額最小值L=100美元。我們可以計算出目標現金餘額C*為

C*=L+（3/4×F×σ²/R）^（1/3）

=100+（3/4×10×40 000/0.01）^（1/3）

=100+30 000 000^（1/3）=100+311=411（美元）

因此，上限U*為

U*=3×C*-2×L=3×411-2×100=1 032（美元）

最後，平均現金餘額為

平均現金餘額=（4×C*-L）/3=（4×411-100）/3=514（美元）

19A.4　BAT和米勒–奧爾模型的含義

兩個現金管理模型的複雜程度不一樣，但是它們有相同的含義。在兩個模型中，假如其他條件相同，我們發現：

（1）利率越高，目標現金餘額越低；

（2）指令處理成本越高，目標現金餘額越高。

這些含義都相當明顯。米勒–奧爾模型的優勢在於它考慮了以淨現金流入的變動衡量的不確定性，從而提升我們對於現金管理問題的理解。

米勒–奧爾模型表明，不確定性（σ²）越大，目標現金餘額和最小現金餘額之差就越大。同樣，不確定性越大，現金餘額上限和平均現金餘額也越高。這些都很直觀。例如，變動越大，餘額降低到下限以下的機會就越高。所以，我們要保持一個較高的現金餘額，以防這種事情的發生。

19A.5　影響目標現金餘額的其他因素

在繼續往下講述之前，我們簡要討論一下影響目標現金餘額的兩個其他因素。

第一，在有關現金管理的討論中，我們假設現金投資在有價證券上，例如國庫券。公司通過出售這些證券獲得現金。另一個選擇是借入現金。借款引入了有關現金管理的其他考慮因素。

（1）由於利率可能會更高，因此借款成本可能比出售有價證券高。

（2）借款的需求取決於管理者是否希望持有低現金餘額。有較大的現金流波動性且在有價證券上投資較少的公司更可能用借款來應對非預期的現金流出。

第二，對於大公司而言，買賣有價證券的交易成本與持有現金的機會成本相比非常小。例如，假設公司有100萬美元現金，在24小時內用不到。這個公司應該將這筆錢投資還是讓它閒置呢？

假設公司可以將這筆錢以7.57%的年利率進行投資。這種情況下的日利率大約為2個基本點（0.02%或0.000 2）。（注：一個基本點是一個百分點的1%。另外，年利率按（1+R）³⁶⁵=1.075 7計算，意味著日利率為0.02%。）因此100萬美元每天賺得的報酬為0.000 2×1 000 000=200美元。在許多情況下，指令處理成本要比這少很多；因此大公司會非常頻繁地購買和出售證券，而不是讓大筆資金閒置。

概念問題

19A.1a　什麼是目標現金餘額？

19A.1b BAT模型中的基本權衡是什麼？

19A.1c 描述米勒–奧爾模型如何運作。

附錄複習和自測題

19A.1　BAT模型　根據下面的信息，用BAT模型計算目標現金餘額：

持有現金的機會成本、交易成本和總成本分別是多少？如果持有15 000美元，這些成本分別是多少？如果持有25 000美元呢？

附錄複習和自測題答案

19A.1　由BAT模型可得，目標現金餘額為

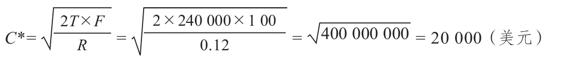
平均現金餘額將會是C*/2=20 000/2=10 000美元。當現行利率是12%時，持有10 000美元的機會成本是10 000×12%=1 200美元。這一年中要下訂單240 000/20 000=12次，所以訂單成本，或者說交易成本是12×100=1 200美元。因此總成本是2 400美元。

如果持有15 000美元，平均餘額為7 500美元。可以驗證這種情況下的機會成本、交易成本和總成本分別是900美元、1 600美元和2 500美元。如果持有25 000美元，這些成本將分別是1 500美元、960美元和2 460美元。

思考和練習題

基礎問題

1.目標現金餘額的變動　指出下列情況分別對公司的目標現金餘額可能會產生何種影響。用字母I表示增加，D表示減少。針對每一種情況簡述你的理由。

a.經紀人收取的佣金降低了。

b.貨幣市場證券的利率上升了。

c.銀行對補償性餘額的要求提高了。

d.公司的信用評級提高了。

e.借款成本增加了。

f.銀行對服務收取直接費用。

2.運用BAT模型　根據下面的信息，用BAT模型計算目標現金餘額：

你如何解釋你的答案？

3.機會成本與交易成本　White Whale公司的日均現金餘額是1 700美元。1年所需的現金總額為64 000美元。利率是5%，每次補充現金的成本是8美元。持有現金的機會成本、交易成本和總成本分別是多少？你認為White Whale公司的策略怎麼樣？

4.成本和BAT模型　Debit and Credit在一年中共需要21 000美元現金用於交易和其他用途。當現金較少時，它就出售1 500美元的證券，轉換成現金。年利率是4%，出售證券的成本為每次25美元。

a.當前政策下的機會成本是多少？交易成本呢？不做額外的計算，你認為Debit and Credit持有的現金太多還是太少？為什麼？

b.用BAT模型計算出的目標現金餘額是多少？

5.確定最優現金餘額　All Day公司目前持有690 000美元現金。它預測下一年每個月的現金流出將比現金流入多140 000美元。當前持有的現金中，應當保留多少？多少應該用於增加公司持有的有價證券？每次通過經紀商買賣證券時，公司支付250美元的費用。貨幣市場證券的年利率是3.2%。用多餘的現金進行初始投資之後，接下來的12個月還要出售多少次有價證券？

6.解釋米勒–奧爾模型　All Night股份有限公司運用米勒–奧爾現金管理法，其下限是43 000美元，上限是125 000美元，目標現金餘額是80 000美元。解釋這些點分別代表什麼；然後解釋這個系統將如何運作。

7.運用米勒–奧爾模型　Slap Shot公司與買賣有價證券相關的固定成本是40美元。現行日利率是0.013%，並且公司估計其每日淨現金流的標準差是80美元。管理層將現金持有的下限設置為1 500美元。請使用米勒–奧爾模型計算目標現金餘額和上限。講述這個系統將如何運作。

8.解釋米勒–奧爾模型　根據米勒–奧爾模型，描述如果淨現金流的變動增加，下限、上限和利差（兩者之間的差距）將會有什麼變化。就為什麼會出現這種變化給出一個直觀的解釋。如果方差降到0，將會有什麼變化？

9.運用米勒–奧爾模型　Pele自行車店每日現金流的方差是890 000美元。公司持有現金的機會成本是每年4.1%。如果公司可承受的下限是160 000美元，那麼目標現金持有水平和上限應該是多少？買賣證券的固定成本是每筆交易300美元。

10.運用BAT模型　Rise Against公司利用BAT模型確定其目標現金餘額為5 100美元。每年需要的現金總額為31 000美元，訂單成本是10美元。Rise Against採用的利率應該是多少？

[1] M.H. Miller and D. Orr,“A Model of the Demand for Money by Firms,” Quarterly Journal of Econonmics, August 1966.