e1 Stephen Ross 公司理財 v12A
14.2 權益成本
為了開始我們對資本成本的討論,我們先從最難的問題開始:什麼是公司的總體權益成本(cost of equity)?之所以說難,是因為沒有辦法直接蒐集到一家公司所有股東對他們的投資所要求的報酬率,我們只能採取某些方法進行估計。本章討論兩種確定權益成本的方法:股利增長模型法和證券市場線法(SML)。
14.2.1 股利增長模型法
估計權益成本最簡單的方法就是運用第8章學習的股利增長模型法。假設公司的股利會以一個固定的比率(g)增長,每股價格P0可以被寫成
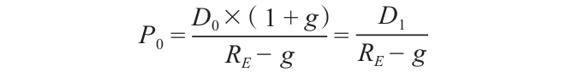
這裡,D0是剛剛支付的股利,D1是下一期的股利。需要注意的是,我們使用RE(E代表權益)來表示股票的必要報酬率。
如我們在第8章所討論的,我們可以整理上式,得出RE如下
RE=D1/P0+g (14-1)
由於RE是股東對於股票所要求的必要報酬率,所以它可以代表公司的權益資本成本。
1.方法的運用
為了運用股利增長模型來估計RE,我們需要3個信息:P0、D0和g。(注:請注意,如果我們已知D0和g,就可以通過D0乘以(1+g)來得到D1。)當然,對於一家公開交易且派發股利的公司,前兩項可以直接觀察到,所以很容易獲得;只有第3項,股利的期望增長率,需要估計。
為了解釋我們怎樣估計RE,假設一家大型公用事業公司GSPS去年每股派發股利4美元,當前股票價格為每股60美元。假設股利將會穩定地以每年6%的比率無限期增長下去,GSPS的權益資本成本是多少?
運用股利增長模型,我們可以計算出來年的預期股利D1為
D1=D0×(1+g)=4×1.06=4.24(美元)
這樣,權益成本RE為
RE=D1/P0+g=4.24/60+0.06=0.130 7,或13.07%
因此權益成本為13.07%。
2.估計g
為了應用股利增長模型,我們必須估計增長率g。有兩種方法:①使用歷史增長率;②使用分析師預測的未來增長率。分析師的預測可以從很多渠道獲得。自然而然,不同渠道會得出不同的估計,所以,有一種方法就是取得多個估計值,然後計算平均值。
此外,我們還觀察先前的股利,比如過去5年的股利,來計算逐年增長率,然後將它們平均。例如,假設我們觀察某一公司的資料如右所示。
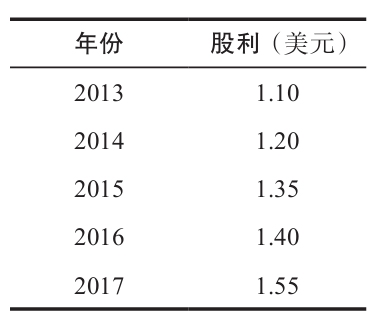
我們可以計算得到每年的股利變化如下:

值得注意的是,我們計算股利變化是以年為基礎的,並且用百分比來表示變動。例如,2014年,股利從1.10美元上升到1.20美元,增長了0.10,它所代表的是0.10/1.10=0.090 9,或9.09%的增長率。
如果我們將4個增長率平均,則結果為(9.09%+12.50%+3.70%+10.71%)/4=9%,所以我們可以用9%作為預期增長率g的估計值。需要注意的是我們計算出的9%增長率是一個簡單的,或者說是算術平均值。回到第12章,我們還可以計算出幾何平均增長率。在這裡,股利歷經4年時間從1.10美元增長到1.55美元。那麼複合的,或者說是幾何增長率是多少呢?看看你是否同意它是8.95%。你可以把它看成一個簡單的有關貨幣時間價值的問題,1.10美元是現值,而1.55美元是終值。
一般來說,幾何平均值(8.95%)比算術平均值(9%)要低,但是這裡的區別並不像一般實務中那麼顯著。一般來說,如果股利過去以相對平穩的速度增長,就如我們運用這種方法時假設那樣,那麼我們按照什麼方法計算平均股利增長率都不會產生太大的差別。
3.方法的優點和缺點
股利增長模型法的最主要優點是簡單。它容易理解且容易運用。但是,它也有許多實際的問題和缺點。
第一個,也是最為顯著的問題是,股利增長模型顯然只適合支付股利的公司。這意味著這種方法在很多情況下都是沒用的。另外,即使對於支付股利的公司,最重要的潛在假設是股利會以固定比率增長,如我們之前案例所闡述的,絕不可能正好出現這個情況。最後,這個模型只適合於那些合理的穩定增長可能會發生的例子。
第二個問題是,估計的權益成本對估計的增長率很敏感。對於一個給定的股票價格,g只要向上增長一個百分點,估計的權益成本至少增長一個整的百分點。因為D1也可能會往上調,所以實際的增長將會更大。
最後,這種方法並沒有明確地考慮風險。不像SML方法(我們將在隨後討論),它對投資的風險並沒有進行直接調整。例如,對所估計的股利增長率的確定性和不確定性並沒有調整餘地。結果,很難說估計的報酬率是否與風險水平相稱。[1]
14.2.2 SML方法
在第13章中,我們討論了證券市場線SML。最主要的結論就是對於一項有風險的投資,必要的或者說預期的報酬率取決於三項因素:
(1)無風險報酬率Rf;
(2)市場風險溢價,E(RM)-Rf;
(3)該資產相對於平均資產而言的系統風險,也就是我們所說的β係數。
應用SML,我們可以將公司權益的期望報酬率寫成
E(RE)=Rf+βE×[E(RM)-Rf]
其中βE是估計的貝塔值。為了使證券市場線模型與股利增長模型保持一致,我們將省略代表期望的E,把SML法下的必要報酬率RE寫成
RE=Rf+βE×(RM-Rf) (14-2)
1.方法的應用
為了運用SML法,我們需要無風險報酬率Rf、市場風險溢價的估計值RM-Rf和相關貝塔係數的估計值βE。在第12章,我們已經看到市場風險溢價的估計值之一(基於大公司的普通股)大約為7%。而在編寫本章時,美國國庫券利率大約是0.40%,所以我們把它作為我們的無風險報酬率。公開交易公司的貝塔係數可以公開取得。[2]
為了說明這一點,我們在第13章中已經看到特斯拉公司的貝塔係數估計值為1.19(見表13-8)。我們因此能夠估計特斯拉的權益成本為
R特斯拉=Rf+β特斯拉×(RM-Rf)=0.004 0+1.19×0.07=0.087 3,或8.73%
因此,運用SML法,我們可以計算出特斯拉的權益成本大概是8.73%。
2.方法的優點和缺點
SML法有兩個很重要的優點。第一,它很清楚地針對風險進行了調整。第二,對並沒有穩定增長的股利的公司也適用。因此,它適用於更為廣泛的情況。
當然,SML法也有缺點。運用SML法需要估計兩個值:市場風險溢價和貝塔係數。如果估計得不準確,那麼得到的權益成本也不準確。例如,我們估計市場風險溢價為7%,是根據一個特定的股票組合大約100年間的報酬率得來的。如果使用不同時期或者不同的股票,就會得出不同的估計值。
最後,與股利增長模型法相同,當我們應用SML模型時,也需要基於過去預測未來。實際上經濟環境變化很快,因此,過去未必能很好地指引未來。在最好的情況下,兩種方法(股利增長模型法和SML法)都是可使用的,而且這兩種方法得出的答案很接近。如果真是如此,我們對估計值應該會有一些信心。我們也希望能夠做一個實際檢驗,將這些結果同其他類似的公司做比較。
【例14-1】權益成本
假設Alpha航空公司的股票貝塔值為1.2。市場風險溢價是7%,無風險報酬率是6%。Alpha去年的股利是每股2美元,預期股利會以8%的速度無限期增長。股票目前的市場售價為30美元。Alpha的權益成本是多少?
我們可以從SML法入手。通過計算,我們發現Alpha航空公司股票的期望報酬率為
RE=Rf+βE×(RM-Rf)=6%+1.2×7%=14.4%
這表明14.4%是Alpha的權益成本。接著我們運用股利增長模型法。預計股利D0×(1+g)=2×1.08=2.16美元,所以用這種辦法得出的期望報酬率是
RE=D1/P0+g=2.16/30+0.08=15.2%
兩種估計值很相近,將其平均我們可以發現Alpha的權益成本大約為14.8%
概念問題
14.2a 當我們說一家公司的權益成本為16%,我們的意思是什麼?
14.2b 估計權益成本的兩種方法分別是什麼?
[1] 對於風險,有一個隱含的調整,這是因為使用的是當前的股票價格。假設其他條件保持不變,風險越大,股票價格就越低。同樣,在假設其他信息相同的情況下,股票價格越低,權益成本就越高。
[2] 貝塔係數可以直接利用歷史數據來估計。關於如何估計的討論,參見:Chapters 10, 11, and 13 in S. A. Ross, R. W. Westerfield, J. J. Jaffe, Corporate Finance, 11th ed. (New York: McGraw-Hill, 2016).