BUSINESS BOOKS

章節複習和自測題

13.1　期望報酬率和標準差　本題旨在讓你練習投資組合績效計量指標的計算。假設有2項資產，3種可能的經濟狀況如下表所示。

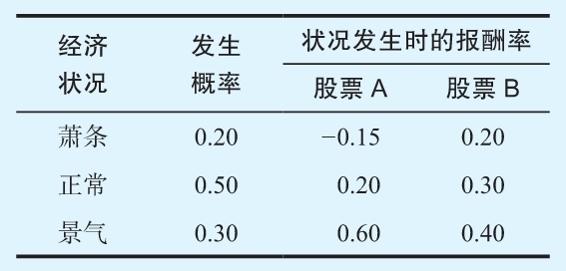
這兩隻股票的期望報酬率和標準差分別是多少？

13.2　投資組合的風險和報酬率　在13.1題中，假設你一共有20 000美元。如果你把15 000美元投資在股票A上，其餘的投資在股票B上，你的投資組合的期望報酬率和標準差分別是多少？

13.3　風險和報酬率　假設你觀察到下列情況：

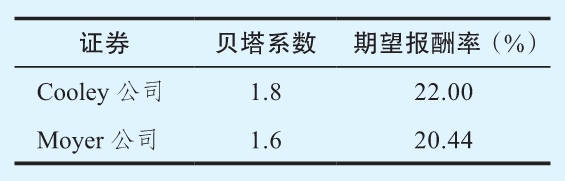
如果無風險報酬率是7%，這些證券有沒有被正確定價？如果它們被正確定價，無風險報酬率應該是多少？

13.4　CAPM　假設無風險報酬率是8%。市場的期望報酬率是16%。如果某一特定股票的貝塔係數是0.7，根據CAPM，該股票的期望報酬率是多少？如果另一隻股票的期望報酬率是24%，它的貝塔係數是多少？

答案

13.1　期望報酬率就是可能的報酬率乘以它們的概率

E（R_A）=（0.20×（-0.15））+（0.50×0.20）+（0.30×0.60）=0.25，或25%

E（R_B）=（0.20×0.20）+（0.50×0.30）+（0.30×0.40）=0.31，或31%

方差則是把距離期望報酬率的偏差的平方與它們的概率的乘積加總起來得到的

σ²_A=0.20×（-0.15-0.25）²+0.50×（0.20-0.25）²+0.30×（0.60-0.25）²

=（0.20×（-0.40）²）+（0.50×（-0.05）²）+（0.30×0.35²）

=（0.20×0.16）+（0.50×0.002 5）+（0.30×0.122 5）

=0.070 0

σ²_B=0.20×（0.20-0.31）²+0.50×（0.30-0.31）²+0.30×（0.40-0.31）²

=（0.20×（-0.11）²）+（0.50×（-0.01）²）+（0.30×0.09²）

=（0.20×0.012 1）+（0.50×0.000 1）+（0.30×0.008 1）

=0.004 9

因而標準差為

σ_A=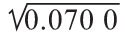=0.264 6，或26.46%

σ_B=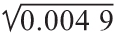=0.07，或7%

13.2　投資組合權重分別為15 000/20 000=0.75和5 000/20 000=0.25。因此期望報酬率為

E（R_P）=0.75×E（R_A）+0.25×E（R_B）=（0.75×0.25）+（0.25×0.31）=26.5%

按照另外一種方法，我們可以計算每一種狀況下的投資組合報酬率：

投資組合的期望報酬率是

E（R_P）=（0.20×（-0.062 5））+（0.50×0.225 0）+（0.30×0.550 0）=0.265，或26.5%

和前面得到的答案一致。

投資組合的方差為

σ²_P=0.20×（-0.062 5-0.265）²+0.50×（0.225-0.265）²+0.30×（0.55-0.265）²=0.046 6

所以標準差是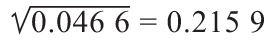：，或21.59%

13.3　如果我們計算風險回報率，就可以得出：Cooley為（22%-7%）/1.8=8.33%，Moyer則為8.4%。相對於Cooley而言，Moyer的期望報酬率太高了，也就是價格太低了。

如果它們都被正確定價，那麼它們的回報與風險之比就必定相等。無風險報酬率R_f必定為：

（22%-R_f）/1.8=（20.44%-R_f）/1.6

稍加計算，我們就會發現無風險報酬率必須是8%

0.2-R_f=（0.204 4-R_f）（1.8/1.6）

0.22-0.204 4×1.125=R_f-R_f×1.125

R_f=0.8%，或8%

13.4　由於市場的期望報酬率是16%，因而市場風險溢價為：16%-8%=8%（無風險報酬率是8%）。第1只股票的貝塔係數是0.70，所以它的期望報酬率是：8%+0.70×8%=13.6%。

對於第2只股票而言，風險溢價是：24%-8%=16%，是市場風險溢價的兩倍，因此，貝塔係數必定正好等於2。我們可以用CAPM來加以證實

E（R_i）=R_f+[E（R_M）-R_f]×β_i

0.24=0.08+（0.16-0.08）×β_i

β_i=0.16/0.08=2.0