BUSINESS BOOKS

12.4　報酬率的變動性：第二個啟示

我們已經看到普通股的逐年報酬率傾向於比長期政府債券的報酬率更具波動性。我們現在討論如何計量這種變動性，以便我們開始考察風險問題。

12.4.1　頻率分佈和變動性

首先，我們可以畫出普通股報酬率的頻率分佈（frequency distribution）圖（見圖12-9）。這裡我們所做的就是計算普通股投資組合的年報酬率落在每一個10%的範圍內的次數。例如，在圖12-9中，在10%到20%的範圍內，17次意味著在91個年回報率中有17個在這個範圍內。

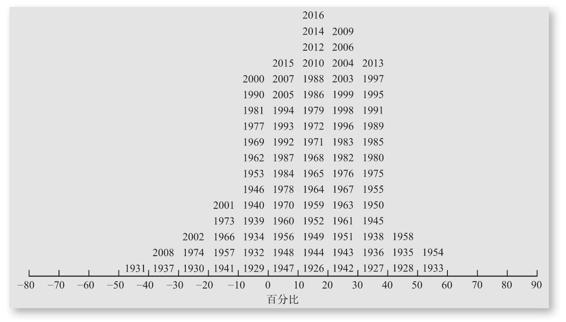
圖12-9　大型公司股票報酬率的頻率分佈（1926～2016年）

資料來源：Morningstar,2017,author calculations.

我們現在需要做的是實際地計量報酬率的分佈情況。例如，我們知道在一個典型的年度中，小型公司股票的報酬率是16.6%。我們現在想要知道實際報酬率與平均報酬率在典型的年度中相差多少。換句話說，我們需要計量報酬率的波動性。應用最廣泛的計量波動性的指標是方差（variance）和它的算術平方根——標準差（standard variance）。我們接下來講述如何計算它們。

12.4.2　歷史上的方差和標準差

方差實質上計量的是實際報酬率和平均報酬率之間的平均平方差。這個數值越大，代表實際報酬率與平均報酬率之間的差異就越大。同樣，方差或標準差越大，報酬率就越分散。

我們計算方差和標準差的方式取決於具體的情況。在這章中，我們考察歷史報酬率，因此在這裡講述的是計算曆史方差和標準差的正確程序。如果我們要考察的是未來報酬率，那麼計算程序就有所不同。這種計算的程序我們將在下一章進行討論。

為了說明如何計算曆史方差，我們假定一項特定投資在過去4年中的報酬率分別是10%、12%、3%和-9%。那麼平均報酬率為（0.10+0.12+0.03-0.09）/4=0.04，或4%。值得注意的是，報酬率實際上從未正好等於4%。實際情況是，第1個報酬率與平均報酬率之間的偏差為0.10-0.04=0.06，第2個報酬率與平均報酬率之間的偏差為0.12-0.04=0.08，依此類推。為了計算方差，我們先計算這些偏差值的平方，再加總起來，然後除以報酬率的個數減去1後的差，在本例中就是除以3。下表展示了大部分信息：

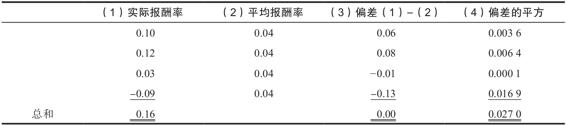
在第1欄中，我們列出了4個實際報酬率。在第3欄中，我們把實際報酬率減去4%，得出實際報酬率和平均報酬率之間的偏差值。最後，在第4欄中，我們將第3欄中的數值進行平方，得到偏差的平方。

現在，我們把偏差的平方和0.027 0除以報酬率的個數減去1的差，就可以計算出方差。用Var（R），或σ²代表報酬率的方差

Var（R）=σ²=0.027/（4-1）=0.009

標準差是方差的平方根。因此，如果用SD（R）或σ代表報酬率的標準差，就會得出結果

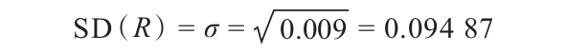
採用方差的平方根是因為方差採用百分比的平方來計量，因此很難解釋。標準差是普通的百分比，因此這裡的答案可以寫成9.487%。

請注意，在上表中，偏差的和等於0。它永遠都是如此，並且為驗算提供了一個好方法。總的來說，如果我們有T個歷史報酬率，這裡的T是某個數字，我們就可以將歷史方差寫成

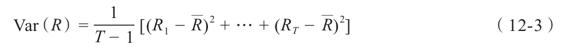
這個公式告訴我們去做前面做過的事情：把T個報酬率（R₁，R₂，…）分別減去平均報酬率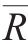；然後將每一個差值進行平方，再將它們加總起來；最後，把這個總和除以報酬率個數減去1，即（T-1）。標準差永遠是方差的平方根。標準差被廣泛地應用於計量波動。

【例12-2】計算方差和平均差

假定Supertech公司和Hyperdrive公司過去4年的報酬率如下：

平均報酬率是多少？方差是多少？標準差是多少？哪一項投資的波動性更大？

為了計算平均報酬率，我們將報酬率相加再除以4。結果是

Supertech公司平均報酬率=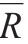=0.70/4=0.175

Hyperdrive公司平均報酬率=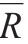=0.22/4=0.055

要計算Supertech公司的方差，我們可以把相關的計算歸集如下：

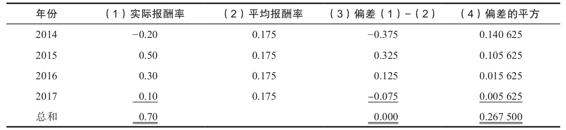
因為有4年的報酬率，我們將0.267 5除以（4-1）=3來計算方差。

作為練習，證實一下你能得出與我們所計算的Hyperdrive公司相同的結果。請注意，Super-tech公司的標準差是29.86%，是Hyperdrive公司的標準差13.28%的兩倍還多。因此，Supertech公司是波動性更大的投資。

12.4.3　歷史記錄

圖12-10總結了我們到目前為止對資本市場歷史的大部分討論。它展示了平均報酬率、標準差和年報酬的頻率分佈。例如，在圖12-10中，小盤股投資組合的標準差（每年31.9%）比國庫券投資組合的標準差（每年3.1%）大10倍以上。我們稍後再討論這些數字。

12.4.4　正態分佈

對許多不同的隨機事件，一種特殊的隨機分佈——正態分佈（normal distribution）或叫作鐘形曲線（bell curve），用於描述事件發生在某一特定範圍內的可能性。例如，“按照曲線打分”後面所隱藏的概念就是來源於考試分數通常呈鐘形曲線分佈這個事實。

圖12-11展示了一個正態分佈以及它獨特的鐘形。可以看出，這個分佈比圖12-10中所示的實際報酬率的分佈圖外觀更加清晰。即便如此，就像正態分佈一樣，實際報酬率分佈圖至少看起來大致是呈山形的，並且是對稱的。如果確實如此，它一般就很近似於正態分佈了。

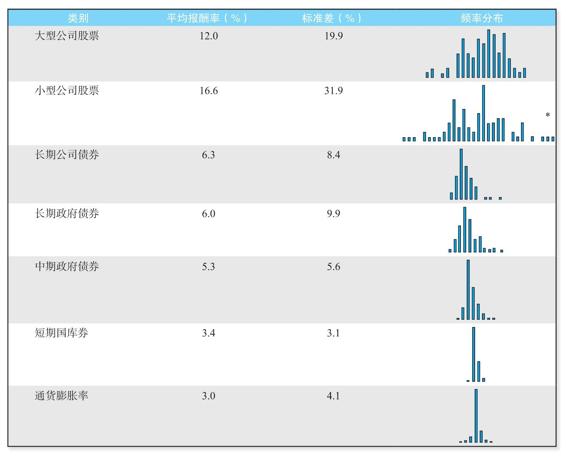
圖12-10　平均報酬率、標準差與頻率分佈（1926～2016年）

注：1933年，小型公司股票的年報酬率為142.9%。

資料來源：Morningstar,2017,author calculations.

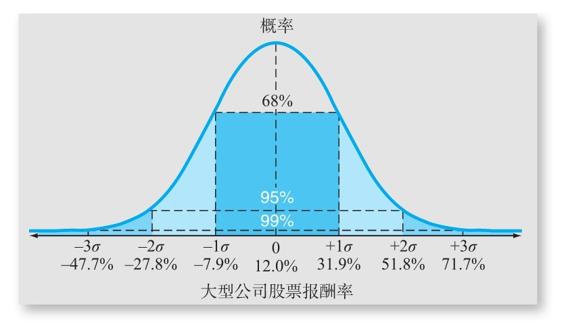
圖12-11　正態分佈

注：本圖所示的報酬率基於一個大型公司普通股票組合的歷史報酬率和標準差。

另外，要記住的是，圖12-10的分佈是根據91個觀測值所形成的。而圖12-11的分佈原則上是要根據無數多個觀察值所形成。如果我們能夠觀察到更多數據，比如說1 000年，我們可以填入許多不同數據，並最終在圖12-10中得到更加平滑的圖像。出於我們的目的，觀察到報酬率至少近似地呈正態分佈就足夠了。

正態分佈的有用性主要源於它完全用平均數和標準差來描述。如果你有這兩個指標的數值，那麼你就不需要其他的東西了。例如，在正態分佈下，結果落在距平均值1個標準差範圍內的概率大約是2/3，落在距平均值2個標準差範圍內的概率大約是95%。最後，落在距離平均值超過3個標準差範圍的概率小於1%。這些概率都展示在了圖12-11中。

為了瞭解它為什麼有用，請回顧圖12-10，大型公司股票的報酬率的標準差是19.9%，平均報酬率是12.0%。所以，如果頻率分佈至少接近正態分佈，那麼某一年的報酬率落在-7.9%到31.9%之間的概率（12%±1個標準差，19.9%）大約是2/3。這些點都標示在圖12-11中。換句話說，報酬率有大約1/3的機會會超出這個範圍。這實際上告訴我們，如果你購買大公司的股票，你應該預期每3年就有1年超出這一範圍。這一點進一步證明了我們前面關於證券市場波動性的認識。然而，報酬率在-27.8%到51.8%之外（12.0%±2×19.9%）的概率大約只有5%，這些點都標示在圖12-11中。

12.4.5　第二個啟示

根據我們對逐年報酬率波動性的觀察，我們得出了資本市場歷史的第二個啟示。通常來說，承擔風險可以帶來可觀的回報，但是在某個給定的年份，股票價值出現戲劇性變化的概率也很大。因此，我們的第二個啟示是：潛在的回報越大，風險就越大。

12.4.6　2008年：值得銘記的一年

為了進一步加深我們對股票市場波動性的認識，考慮就在短短几年前，2008年，作為美國歷史上對於股票投資者來說最差的一年，被記入了史冊。那麼情況究竟有多差呢？正如在本章中（如表12-1）所列示的，應用最廣泛的標準普爾500指數下跌37%。在500只股票中，485只股票在當年下跌。

1926～2016年，只有1931年出現過報酬率比2008年低的情況（-44%對比-37%）。更糟的是，在2009年1月報酬率繼續下滑了8.43%。從2007年11月（開始下跌的時間）到2009年的3月（下跌結束的時間），標準普爾500指數總共下跌了50%。

圖12-12列示了2008年標準普爾500指數的逐月表現情況。正如圖中所展示的，在12個月中有8個月的報酬率為負。大多數的損失發生在秋季，尤其是僅10月份1個月投資者就損失了17%。小盤股的情況也不容樂觀。它們同樣在一年當中損失了37%（在10月份下跌了21%），這是自從1937年下跌了58%之後的最差表現。

正如圖12-12所暗示的，股票價格在1年中的波動性很大。奇怪的是，標準普爾指數正好有126天上升、126天下降（記住，證券市場在週末和假期關閉交易）。當然，下降那些天的情況通常更糟。為了觀察2008年報酬率的波動性有多不尋常，我們看到有18天的標準普爾的價值改變了5%以上。而1956～2007年只有17天出現過這樣的波動。

股票價格的下跌是一個全球現象，世界許多主要證券市場的下跌幅度大大高於標準普爾指數。例如，中國、印度和俄羅斯，都經歷了高於50%的下跌。小小的冰島更是遭遇了1年中報酬率下跌高於90%的情況。冰島的證券交易也在10月9日被暫停。在10月14日交易重新開始的那天，股票仍舊下跌76%，這一天成為現代的一個紀錄。

難道2008年對於美國的投資者就沒有亮點了嗎？答案是，有的，因為雖然股票淪陷，但是債券飆升，尤其是美國國庫券。事實上，長期國庫券賺取了40%，而短期國庫券也上升了13%。長期公司債券表現相對較差，但是也努力落在正數的範圍內，上升了9%。這些報酬率是在假設以CPI衡量的通貨膨脹率實際上為零的情況下考慮的。

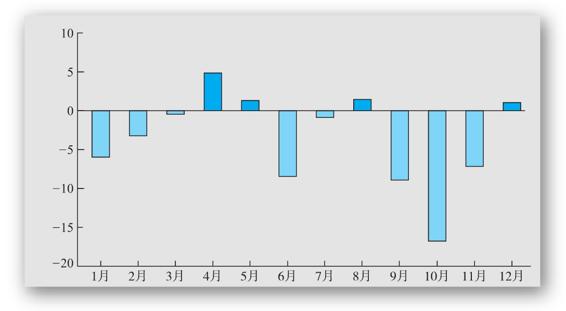
圖12-12　2008年標準普爾500指數月度報酬率

當然，股票價格可以在兩個方向發生波動。從2009年3月到2011年2月，這700多天的時段裡，標準普爾指數在價值上翻了一倍。這次上升是自從1936年出現了500天時段的股票價格翻番以來最快速的一次翻番。因此，從這一段最近的、非常混亂的資本市場歷史中投資者能得到什麼經驗教訓呢？第一，最明顯的，股票有很大的風險！第二點教訓也非常重要，股票風險的大小取決於具體的組合，多樣化的股票和債券組合在2008年雖然遭遇了損失，但是與全部是股票的投資組合相比，它的損失小得多。換句話說，應將投資分散化，這是我們下一章要詳細考察的一個重點。

12.4.7　利用資本市場的歷史

根據本部分的討論，你應該開始對投資的風險和回報有一定的認識了。例如，在2017年年初，美國國債的收益率約為0.4%。假定我們有一項投資，我們認為它的風險和大型公司普通股投資組合的風險相當。那麼，這項投資的報酬率至少要達到多少才能使我們感興趣？

從表12-3可以看出，大型公司股票的歷史風險溢價是8.6%，所以我們對於必要報酬率的合理估計應該是風險溢價加上國債利率，即0.4%+8.6%=9%。這可能會讓你感到興奮。但如果我們正在考慮開始一項新的業務，那麼這麼做的風險可能類似於投資於小盤股。在這種情況下，該風險的歷史溢價為13.2%，因此，這項投資我們可能至少需要13.6%的回報。

我們將在下章詳細討論風險和必要報酬率之間的關係。現在，你應該注意的是，一個風險性投資的預計內部報酬率（IRR）介於10%～20%，並不是特別突出。它取決於風險的大小。這也是來自資本市場的一個重要啟示。

【例12-3】投資成長股

成長股（growth stock）這個術語經常是小盤股的代名詞。這種投資適合於“寡婦和孤兒”嗎？在給出答案前，你應該考慮歷史波動性。例如，從歷史紀錄中來看，如果你購買一個這種公司的投資組合，在一個單獨的年度中，實際損失15%或更多的近似概率是多少？

回顧表12-10，我們發現小盤股的平均報酬率為16.6%，標準差是31.9%。假設報酬率接近正態分佈，那麼你的報酬率落在-15.3%到48.5%（16.6%±31.9%）這個區間的概率大約為1/3。因為正態分佈是對稱的，在這個範圍之上和之下的機會是均等的。因此你有1/6（1/3的一半）的可能將會損失超過15.3%。因此，你應該預期到這種情況平均每6年會出現一次。這樣，這種投資的波動性較大，因而不太適合那些不能承受這種風險的人。

12.4.8　對股市風險溢價的進一步分析

正如我們前面所討論的，在歷史上股市的風險溢價已經相當大。事實上，在標準經濟模型的基礎上，有人認為歷史風險溢價過大，如果作為對未來風險溢價的估計，可能過高了。

當然，任何時候當我們用過去來預測未來時，都存在著這樣一種風險，即我們觀察的過去的一個時段無法代表未來。例如，在本章中，我們研究了1926～2016年這個時段。可能在這個時段的投資者碰到了好運從而獲取了高額的報酬率。更早的數據也是可以獲得的，儘管數據的質量不同。考慮到這一點，研究人員追溯到了1802年的回報，1926年以前的風險溢價也許相對更小，但是並不顯著。

另一種可能是美國的股市出奇的好，至少其他一些主要國家的投資者沒能得到這麼好的報酬率，因為它們的金融市場由於革命、戰爭或惡性通貨膨脹的因素，幾乎或者完全崩潰。最近的一項研究通過調查17個國家1900～2005年的數據，探討了這個問題。

圖12-13列示了所有17個國家在106個年度的歷史平均股市風險溢價。美國的風險溢價以7.4%（因為考察的時間段不同，因此該結果與我們早期的預計不同）高居第8位。整體平均風險溢價為7.1%。這些數字清晰地表明美國投資者做得不錯，但是與其他國家的投資者相比並不突出。

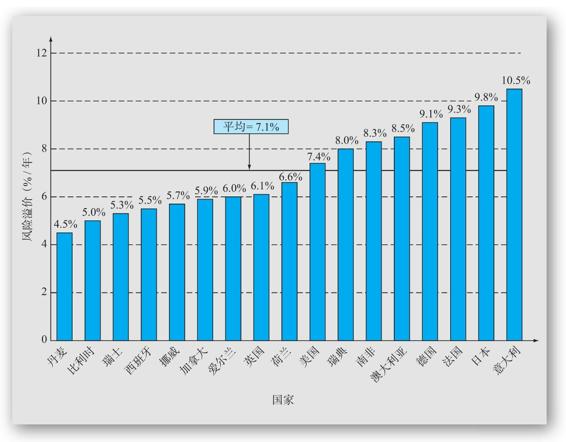
圖12-13　1900～2005年17個國家的股市風險溢價

資料來源：Based on information in Elroy Dimson,Paul Marsh,and Michael Staunton,“The Worldwide Equity Premium:A Smaller Puzzle,”in Handbook of the Equity Risk Premium,Rajnish Mehra,ed.（Elsevier:2007）.

那麼，1926～2016年美國股票市場的風險溢價是否被高估？證據似乎表明，答案是“可能有一點”。到目前為止，有一件事我們沒有強調：即使使用了106年的數據，但是對平均風險溢價的測量仍然不是非常精確。從統計的角度來看，所估計的美國的風險溢價7.4%的標準誤差大約為2%（注：回憶下統計學的基礎知識中關於樣本均值的標準差的算法是樣本標準差除以樣本個數的平方根。在本例中，1900～2005年的標準差為19.6%，因此，標準誤差是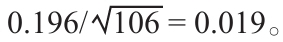）。因此，即使一個單位標準誤差的範圍也在5.4%～9.4%。

概念問題

12.4a　如何計算方差、標準差？

12.4b　正態分佈中，比均值少一個標準差的概率是多少？

12.4c　假設長期公司債券呈近似的正態分佈，那麼某一年度報酬率為14.6%或以上的近似概率為多少？對於國庫券，這個概率是多少？

12.4d　資本市場歷史上的第二個啟示是什麼？