e1 Stephen Ross 公司理財 v12A
11.4 經營現金流量、銷售量和盈虧平衡
在進行項目分析時,會計盈虧平衡是一種非常有用的工具。然而,我們最終更加關心的是項目的現金流量而不是會計利潤。因此,舉例來說,如果銷售量是關鍵的變量,那麼,我們需要更多地瞭解銷售量和現金流之間的關係,而不只是會計收支平衡。
在本節中,我們的目標是說明經營現金流量和銷售量之間的關係。我們還討論了一些計量盈虧平衡的其他方法。為了簡化問題,我們將忽略稅的影響。首先考察的是會計盈虧平衡和現金流量之間的關係。
11.4.1 會計盈虧平衡和現金流量
既然我們已經知道如何找出會計盈虧平衡點,自然而然就會聯想其與現金流量之間的關係。為了說明問題,假設Wettway帆船公司正在考慮是否推出新的Margo級帆船。該類帆船每艘售價為40 000美元,變動成本約為售價的一半,即20 000美元,固定費用為每年50萬美元。
1.基本情況
該項目所需的總投資為350萬美元。這筆投資將在設備5年的使用期限內以直線法線折舊完畢。殘值為零,並且不需要額外增加營運資本。Wettway公司對新項目要求的必要報酬率為20%。
根據市場調查和歷史經驗,Wettway預計在未來5年總共出售425艘帆船,即每年85艘。如果不考慮稅的影響,是否應該推行這個項目?
不考慮稅的影響,每年85艘帆船帶來的經營現金流量為
經營現金流量=息稅前收益+折舊-稅費=(S-VC-FC-D)+D-0
=85×(40 000-20 000)-500 000=1 200 000(美元/年)
在20%的必要報酬率下,5年的年金係數為2.990 6,因此,NPV為
NPV=-3 500 000+1 200 000×2.990 6=-3 500 000+3 588 735=88 735(美元)
如果沒有其餘的補充信息,那麼依據以上結果應該採納這個項目。
2.計算盈虧平衡水平
進一步考察這個項目,你可能會提出一系列問題。例如,從會計計量角度出發,Wettway公司需要出售多少艘新帆船才能達到盈虧平衡?如果Wettway達到盈虧平衡,那麼該項目每年產生的現金流量為多少?此時該項投資的報酬率為多少?
在考慮固定成本和折舊之前,Wettway公司每艘帆船帶來的現金流入為40 000-20 000=20 000美元(收入減去變動成本)。折舊為每年3 500 000/5=700 000美元。固定成本和折舊每年合計為120萬美元,所以Wettway每年需要出售(FC+D)/(P-v)=120/2=60艘帆船,才能達到會計意義上的盈虧平衡。這比每年預計的銷售量要少25艘。因此,假定Wettway公司確定實際值必將落在預測值的上下15艘的波動範圍內,那麼這個新的投資項目無法達到會計盈虧平衡點的可能性就微乎其微了。
要計算Wettway公司在該情況下的現金流量,我們注意到,當每年的銷售量為60艘時,淨利潤恰好為零。回顧前面的章節,經營現金流量可以表示為淨利潤加上折舊(逆推法的定義),那麼,此時的經營性現金流量就等於折舊,也是就是本例中的70萬美元,內部報酬率恰好為0。(為什麼?)
3.投資回收期和盈虧平衡
正如我們在前面例子中所說明的那樣,當一個項目在會計意義上達到盈虧平衡時,該期間的現金流量就等於折舊。這一結果在會計意義是合理的。例如,假設我們在一個5年期項目上投資10萬美元。按直線法折舊至零,那麼每年的折舊為2萬美元。如果該項目每一期都恰好達到盈虧平衡,那麼每期的現金流量就是2萬美元。
這個項目在運行年限內的現金流量之和為5×2萬美元=10萬美元,也就是初始投資額。這表明,如果該項目每一期都恰好達到盈虧平衡,那麼項目的投資回收期剛好等於其運行的年限。同樣,如果一個項目的銷售量超過了盈虧平衡點,那麼它的投資回收期就比運行年限短,而且投資的報酬率為正。
不過,如果項目恰好在會計意義上達到盈虧平衡,那麼它的NPV為負,並且報酬率為0。對於前面的帆船項目,Wettway幾乎肯定能夠在會計意義上達到盈虧平衡,這至少讓人覺得有點安慰,因為這意味著公司的“下行”風險(其潛在的損失)是有限的,但我們仍然不知道該項目是否真的有利可圖,還需要進一步的研究。
11.4.2 銷售量和經營現金流量
此時,我們將例子一般化,並引進其他的一些盈虧平衡計量方法。根據上一節的討論,我們知道,在不考慮稅的情況下,項目的經營現金流量(OCF)可以簡化為息稅前利潤加折舊
OCF=[(P-v)×Q-FC-D]+D=(P-v)×Q-FC (11-2)
對於Wettway公司的帆船項目,經營現金流量和銷售量之間的一般關係可以表示為
OCF=(P-v)×Q-FC=(40-20)×Q-500=-500+20×Q
由此可知,經營現金流量和銷售量之間的關係可以由一條斜率為20,y軸截距為-500的直線給出。如果將銷售量變為幾個不同的數值,可得:

這些點就描繪在圖11-5中,在圖中,我們列示了3個不同的盈虧平衡點。接下來我們對此展開討論。
11.4.3 現金流量、會計盈虧平衡點與財務盈虧平衡點
根據前文的討論可知,經營現金流量和銷售量的關係表示為(不考慮稅的影響):
OCF=(P-v)×Q-FC
整理上式,可求出Q
Q=(FC+OCF)/(P-v) (11-3)
由此可知為獲得任何給定的OCF所需的銷售量(Q)。因此,這個結果比會計盈虧平衡點具有更普遍的意義。我們利用這個式子求出圖11-5中幾個不同的盈虧平衡點。
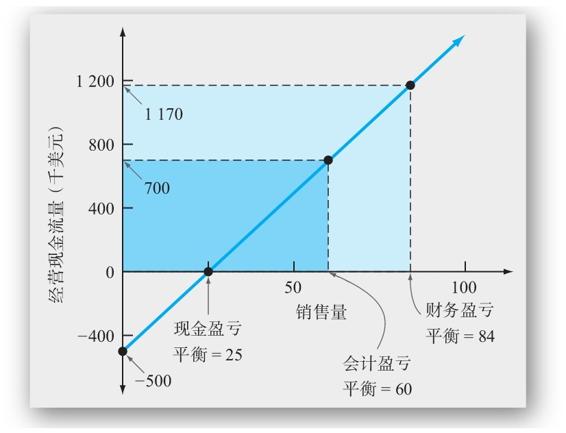
圖11-5 經營現金流量和銷售量
1.再談會計盈虧平衡
根據圖11-5,假設經營現金流量等於折舊(D)。回想起與這種情況相對應的就是會計意義上的盈虧平衡點。為了求出此時的銷售量,我們將700 000美元的折舊代入式子中的OCF
Q=(FC+OCF)/(P-v)=(500 000+700 000)/20 000=60(艘)
這和我們前面所求出的數量一致。
2.現金盈虧平衡
我們已經知道,當達到會計意義上的盈虧平衡點時,淨利潤為0,但是此時的現金流量依然為正。然而,在某個低於會計盈虧平衡點的銷售量上,經營現金流量實際上為負值。這顯然是一個令人不愉快的情形。如果真的發生了,那麼實際上我們需要追加現金來保證項目的運營。
要計算現金盈虧平衡點(cash break-even),即經營現金流量為0時的銷售量,我們將0代入OCF
Q=(FC+OCF)/(P-v)=500 000/20 000=25(艘)
因此,Wettway公司至少需要銷售25艘帆船才能補償50萬美元的固定成本。如圖11-5所示,這一點就是經營現金流量線和橫軸相交的地方。
需要注意到,在現金流意義上達到盈虧平衡點的項目能夠補償它自身的全部固定經營成本,但也只能這樣了。企業無法從項目中獲取任何回報,因此,初始投資全部成了損失(IRR為-100%)。
3.財務盈虧平衡
我們考慮的最後一種情形是財務盈虧平衡點(financial break-even),也就是使淨現值為0的銷售量。對於財務經理而言,這是其最感興趣的情形。我們首先需要確定什麼樣的經營現金流量才能使得淨現值為零,然後再根據這個金額求出銷售量。
為了說明這個問題,回想一下,Wettway公司對其350萬美元初始投資要求的報酬率為20%。當我們考慮到每年20%的機會成本時,Wettway需要銷售多少艘帆船才能達到盈虧平衡呢?
帆船項目的年限為5年。當經營現金流量的現值等於初始投資額350萬美元時,該項目的NPV為零。由於每年的現金流量都相同,因此,我們不妨將其視為普通年金來求出這個未知數。在20%的貼現率下,5年期年金係數為2.990 6,因此OCF可通過如下等式確定
3 500 000=OCF×2.990 6
OCF=3 500 000/2.990 6=1 170 000(美元)
因此,Wettway公司每年需要117萬美元的經營現金流量才能達到財務盈虧平衡。現在,我們可以將OCF代入等式中求出銷售量
Q=(500 000+1 170 000)/20 000=83.5(艘)
所以,Wettway公司每年需要銷售84艘帆船,這不是一個好消息。
如圖11-5所示,財務盈虧平衡點大大高於會計盈虧平衡點。實際情況通常如此。此外,我們還發現,帆船項目的預測風險相當高。我們預計每年銷售量為85艘,但需要84艘的銷售量才能賺取我們所需的報酬率。
4.結論
總體而言,Wettway公司的帆船項目無法達到會計盈虧平衡點的概率非常小。然而,該項目實際的NPV為負值的可能性似乎又特別高。這說明僅僅考慮項目的會計盈虧平衡點是十分危險的。
那麼Wettway公司應該怎麼做呢?新項目就一無是處嗎?這本質上是一個管理問題——做判斷。關鍵的問題是:
(1)我們對預測有多大的信心?
(2)該項目對公司的未來的重要性有多大?
(3)如果銷售量很低,公司受到的傷害有多大?在這種情況下,公司還有其他的選擇嗎?
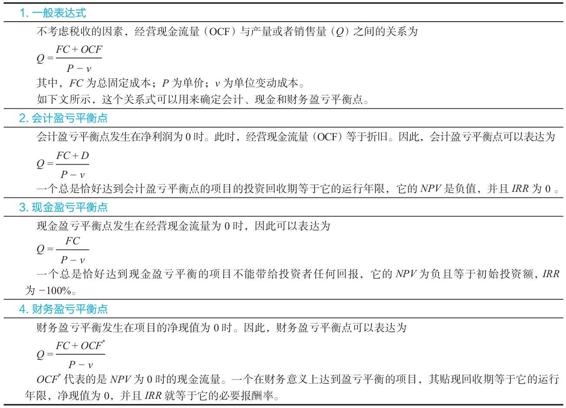
我們在後面的章節將會考慮這些問題。表11-1彙總了我們所討論的各類盈虧平衡點指標,以備未來參考。
表11-1 盈虧平衡指標的總結
概念問題
11.4a 如果一個項目在會計意義上達到盈虧平衡,那麼它的經營現金流量為多少?
11.4b 如果一個項目在現金意義上達到盈虧平衡,那麼它的經營現金流量為多少?
11.4c 如果一個項目在財務意義上達到盈虧平衡,那麼它的貼現回收期為多久?