BUSINESS BOOKS

8.1　普通股估價

普通股估價的實際操作比債券估價更困難，其原因至少有三點。第一，對於普通股而言，無法事先知道任何允諾的現金流量。第二，由於普通股沒有到期日，普通股投資實質上是無限期的。第三，沒有辦法很容易地觀察到市場上的必要報酬率。儘管如此，就像我們將會看到的那樣，在一些情形下，仍然可以得出普通股的未來現金流量的現值，進而確定其價值。

8.1.1　現金流量

假如你正在考慮買一隻股票，並打算1年後把它賣掉。通過一定的渠道得知屆時股票的價值為70美元。你預測這隻股票還會在年末派發每股10美元的股利。如果你要求投資回報率為25%，那麼，你最多願意花多少錢購買這隻股票呢？換句話說，當利率為25%時，期末價值70美元且附帶10美元現金股利的股票的現值是多少？

如果你今天買下這隻股票，1年後賣掉，屆時你將擁有現金總計80美元。在25%貼現率下

現值=（10+70）/1.25=64（美元）

因此，你今天最多願意花64美元買這隻股票。

一般來說，令P₀為股票的當前價格，P₁為股票1期後的價格。若D₁為期末派發的現金股利，則

P₀=（D₁+P₁）/（1+R）　（8-1）

式中，R是市場對這項投資所要求的必要報酬率。

請注意，實際上到此我們還沒有討論得很透徹。如果想要知道今天的股價（P₀），我們就必須首先知道股票1年後的價格（P₁）。這就更難了，所以我們把問題複雜化了。

1期後股票價格P₁是多少呢？通常我們並不知道。但是，假定由於某種原因我們知道2期後的價格P₂。若給定的2期後的預期股利為D₂，1期後的股票價格就是

P₁=（D₂+P₂）/（1+R）

如果我們把這個式子代入P₀的表達式中，就能得到

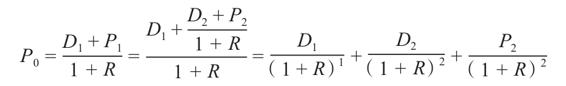
現在我們需要知道第2期的價格。可是我們也不知道它是多少，可以再次進行推導得出

P₂=（D₃+P₃）/（1+R）

如果我們用這個式子代替P₂，就得到

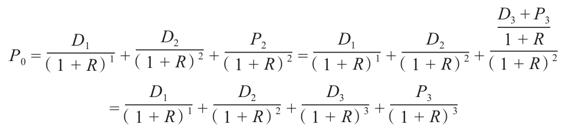
你應該已經開始注意到，我們可以把估計股價的問題無限推至未來。注意，不論股票價格是多少，只要把股票的出售向前推得足夠遠，其現值實際上都會接近於零。^[1]最後我們得到的結果就是，當前股價可以表示成從某一期開始並趨向無限期的一系列股利的現值

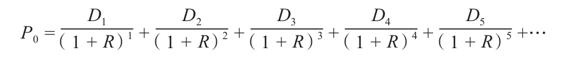
我們在這裡解釋了當前股票價格等於未來所有股利的現值。但是，未來有多少股利呢？從原則上講，有無限多。這意味著我們仍然無法算出股價，因為我們必須預測出無限多股利，然後再把它們貼現。在下一個部分，我們看看有關這個問題的一些特例。

【例8-1】成長股

你可能會對那些目前沒有派發股利的公司，例如Alphabet，持懷疑態度。小型的成長公司通常不派發股利，而是全部進行再投資。那麼，這種股票是不是就毫無價值呢？不一定。當我們說股價等於所有未來股利的現值時，我們並不排除其中有些股利是0的可能，只要不是全部股利都等於0。

假設有一家公司，它在公司章程中規定永遠禁止派發股利。這家公司永遠不借錢，永遠不以任何形式把錢發給股東，也永遠不出售任何資產。這種公司實際上是不可能存在的，因為美國國稅局（IRS）並不喜歡這種公司，而只要股東願意，他們永遠可以通過投票來修改章程。然而，如果確實有這種公司存在，它的股價將是多少呢？

這種股票一定分文不值。這種公司是財務“黑洞”。錢投入之後，沒有任何有價值的東西產生。因為沒有人會從這種投資中得到任何報酬，因此，這種投資是沒有價值的。這個例子有些荒謬，但是它說明，當我們說一家公司不派發股利時，指的是它目前不派發股利而已。

8.1.2　幾個特例

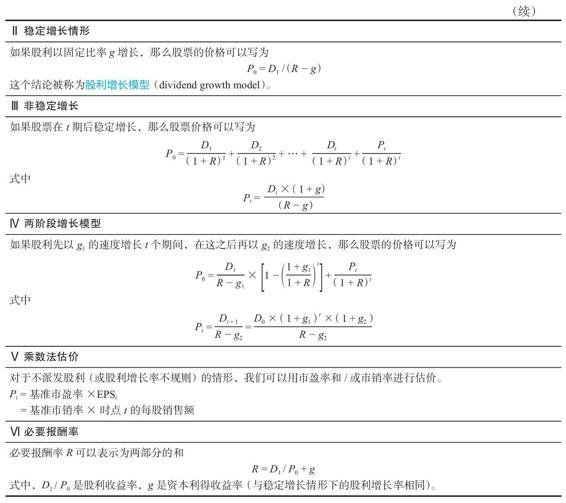
在一些有用的特殊情形下，我們可以得出股票的價值。我們要做的是對未來股利派發模式做一些簡化的假設。在這裡，我們考慮如下3種情形：①股利呈零增長；②股利呈穩定增長；③一段時間後股利呈穩定增長。我們分別考慮這3種情形。

1.零增長

我們已經看過零增長的情形。擁有固定股利的普通股就像優先股一樣。從第6章（例6-7）中，我們知道優先股的股利是固定的，也就是股利呈零增長。對於零增長的普通股而言，這意味著

D₁=D₂=D₃=D=常數

因此，股票的價值為

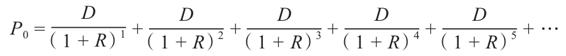
因為股利永遠是等值的，股票可以被視為每期現金流量等於D的普通年金。因此，每股價值為

P₀=D/R　（8-2）

式中，R是必要報酬率。

舉個例子，假定Paradise Prototyping公司的股利政策是每年每股派發10美元的股利。如果這個政策將無限期地持續下去，當必要報酬率為20%時，每股價值是多少？在這種情形下，股票就相當於一種普通年金，因此，每股股價是（10/0.20=）50美元。

2.穩定增長

假定我們知道某家公司的股利總是以固定的比率增長。假設這個增長率為g。如果D₀為剛剛派發的股利，那麼下一期的股利D₁為

D₁=D₀×（1+g）

2期後的股利為

D₂=D₁×（1+g）=[D₀×（1+g）]×（1+g）=D₀×（1+g）²

我們可以重複這個過程來計算未來任何時點的股利。總的來說，通過第6章中我們對複利增長的討論，我們知道未來t期後的股利D_t等於

D_t=D₀×（1+g）^t

就像我們之前看到的一樣，現金流量以某一個固定的比率永遠增長的資產被稱為增長型永續年金（growing perpetuity）。

這種股利穩定增長的假定可能會讓你感到奇怪。為什麼股利會以固定的比率增長呢？這是因為大部分公司都以股利實現穩定增長為明確的目標。例如，2016年，個人護理和家居用品生產商寶潔公司的股利增長了1.0%，增加到每股2.68美元。這個增長之所以值得一提，是因為它是連續第60次出現了。股利的增長屬於股利政策的範疇，我們將會在後面的章節中進一步討論。

【例8-2】股利增長

Hedless公司剛派發了每股3美元的股利。該公司的股利以每年8%的固定比率增長。根據以上信息，5年後該公司的股利是多少？

這裡我們已知當前股利為3美元，未來5年中每年以8%的速度增長。終值為

3×1.08⁵=3×1.469 3=4.41（美元）

因此，在未來的5年裡，股利將增加1.41美元。

如果股利以一個固定的比率增長，那麼我們就已經把預測無限期未來股利的問題，轉化為單一增長率的問題，這是一個很大的簡化。在這種情況下，如果D₀是剛剛派發的股利，g是穩定增長率，則股價可以寫為

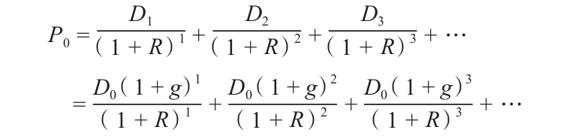
只要增長率g小於貼現率R，這一系列現金流量的現值就是

這個簡潔的結果有很多不同的名稱。我們稱它為股利增長模型（dividend growth model）。不管它叫什麼名稱，它使用起來容易。例如，假設D₀是2.30美元，R是13%，g是5%，則每股價格為

P₀=D₀×（1+g）/（R-g）=2.3×1.05/（0.13-0.05）

=2.415/0.08=30.19（美元）

實際上，我們可以利用股利增長模型得出任何時點的股價，而不僅限於今天。通常，時點t的股票價格為

在我們的例子中，假定我們想知道5年後的股價P₅，我們首先需要知道5年後的股利D₅。因為剛剛派發的股利為2.30美元，每年的增長率為5%，則D₅為

D₅=2.30×1.05⁵=2.30×1.276 3=2.935（美元）

根據股利增長模型，5年後的股價為

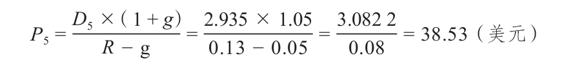
【例8-3】Gordon Growth公司

Gordon公司下一次將派發每股4美元的股利。投資者對Gordon這樣的公司要求16%的報酬率。Gordon公司的股利每年增長6%。根據股利增長模型，Gordon公司的股票目前價值多少？4年後的價值是多少？

這裡要注意的是，下一次的股利D₁是4美元，因此我們不需再乘以（1+g）了。因此，每股股價是

P₀=D₁/（R-g）=4/（0.16-0.06）=4/0.10=40（美元）

因為我們已經知道1年後的股利，因此4年後的股利是D₁×（1+g）³=4×1.06³=4.764美元。4年後的價格是

P₄=D₄×（1+g）/（R-g）=4.764×1.06/（0.16-0.06）

=5.05/0.10=50.50（美元）

請注意，在本例中，P₄等於P₀×（1+g）⁴

P₄=50.50=40×1.06⁴=P₀×（1+g）⁴

要知道為什麼如此，首先請注意

P₄=D₅/（R-g）

然而，D₅恰好等於D₁×（1+g）⁴，所以，P₄可以寫成

P₄=D₁×（1+g）⁴/（R-g）=[D₁/（R-g）]×（1+g）⁴

=P₀×（1+g）⁴

最後一個例子說明了股利增長模型隱含這樣一個假設：股價會以和股利一樣的穩定增長率增長。這一點不足為奇，它只是告訴我們，如果一項投資的現金流量以一個穩定的增長率增長，那麼，該項投資的價值也會以同樣的增長率增長。

也許你想知道，如果股利增長率g大於貼現率R，股利增長模型會變成什麼樣子呢？因為

R-g小於零，所以股票價格似乎會變成負數。然而，這種情形是不會發生的。

相反，如果固定的股利增長率大於貼現率，股票價格會變成無窮大。這是為什麼呢？如果股利增長率比貼現率大，那麼股利的現值會越來越大。實際上，如果股利增長率等於貼現率，也是一樣的情形。在這兩種情形下，用股利增長模型來取代無限個股利的簡化方法是“不合法的”，因此我們從股利增長模型得到的答案是毫無意義的，除非股利增長率小於貼現率。

最後，從穩定增長的情形所得出的表達式適用於所有增長型永續年金，而不只是普通股股利。就像我們在第6章中所看到的一樣，假定C1是增長型永續年金的下一期現金流量，那麼，現金流量的現值為

現值=C₁/（R-g）=C₀×（1+g）/（R-g）

請注意，這個表達式看起來和普通永續年金很像，只不過分母是R-g，而不是R。

3.非穩定增長

我們考慮的下一種情形是非穩定增長。考慮這種情形主要是因為它允許股利在某一段有限的時間內“超常”增長。就像剛剛討論過的一樣，股利增長率不能無限期地大於必要報酬率，但在某段時間內的確是有可能的。為了避免不得不預測並貼現無限個股利的問題，我們要求股利從未來某個時候開始以固定的比率增長。

舉一個簡單的非穩定增長的例子。假如一家公司目前不派發股利，你預測它會在5年後第一次派發股利，股利將會為每股0.5美元，並且你預測股利將會以每年10%的增長率無限期地增長。已知同類公司的必要報酬率為20%。那麼，該公司目前的股票價格為多少？

要計算該公司股票目前的價格，我們首先要求出剛開始派發股利時的股票價格。然後計算出這個未來價格的現值，就可得到股票今天的價格。第一次派發股利是在5年後，此後股利穩定增長。利用股利增長模型，我們可以說4年後的股價為

P₄=D₄×（1+g）/（R-g）=D₅/（R-g）=0.50/（0.20-0.10）=5（美元）

4年後股票價格是5美元，那麼我們就可以以20%的貼現率將它向前貼現4年求出現值

P₀=5/1.20⁴=5/2.073 6=2.41（美元）

這隻股票目前的價值為2.41美元。

在非穩定增長模型中，如果前幾年的股利不是0，那麼問題就會稍微複雜一些。例如，假設你對接下來3年的股利預測如下表所示。

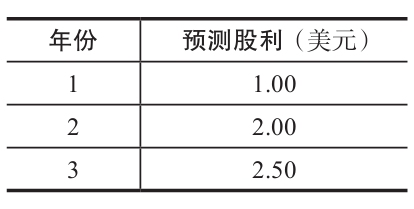
3年後，股利將以每年5%的增長率穩定增長。必要報酬率是10%。目前這隻股票價值多少？

在處理非穩定增長問題時，時間軸將會很有用。圖8-1的時間線描述的就是這個問題。最重要的是要注意穩定增長開始的時間。如圖所示，針對這個問題，穩定增長是從時點3開始的。這意味著我們可以用穩定增長模型來確定時點3的股票價格P₃。到此為止，在這些情況下最常見的錯誤是，不能正確地確定穩定增長階段開始的時間，結果就是在錯誤的時間點計算未來的股票價格。

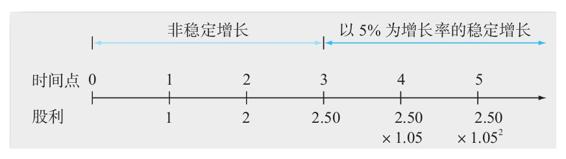
圖8-1　非穩定增長（單位：美元）

股價總是等於未來所有股利的現值。要計算出這個現值，就像先前的做法一樣，首先要計算出3年後的股票價格的現值。然後，再加上這3年之間股利的現值。因此，3年後的價格為

P₃=D₃×（1+g）/（R-g）=2.50×1.05/（0.10-0.05）=52.50（美元）

我們現在用前3年的股利現值加上時點3的股票價格P3的現值，計算出該股票的總價值

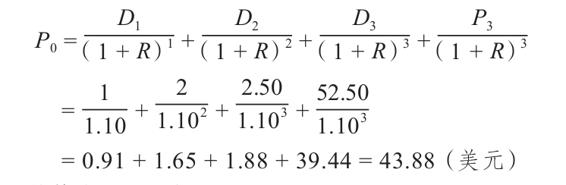
所以，股票今天的價值為43.88美元。

【例8-4】超常增長

Chain Reaction公司因為迅速的擴張和爆炸式的銷售，一直以每年30%的速度增長。你相信這種增長率會持續3年，然後下降到每年10%。如果在那之後增長率永遠維持在10%，那麼股票的總價值是多少呢？剛剛派發的股利總額為500萬美元，必要報酬率為20%。

Chain Reaction公司的情況是一個超常增長的例子。30%的增長率是不可能維持太久的。要評估這家公司的權益價值，我們首先必須計算出超常增長期的股利總額（見下表）。

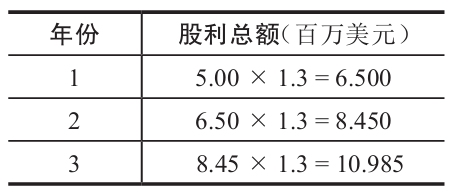
在時點3的價格為

P₃=D₃×（1+g）/（R-g）

其中，g是長期增長率。因此，我們得到

P₃=10.985×1.10/（0.20-0.10）=120.835，即12 083.5萬美元

要計算當前的價格，我們需要用P3的現值加上全部股利的現值

今天股票的總價值為8 758萬美元。如果總共有2 000萬股，那麼每股價值為8 758萬美元/2 000萬股=4.38美元。

4.兩階段增長

我們考慮的最後一種情形是非穩定增長的一個特殊的例子：兩階段增長模型。這種情形說的是股利以g₁的增長率增長t年，隨後無限期地以g₂的增長率增長。在這種情形下，股票的價值可以寫成如下形式

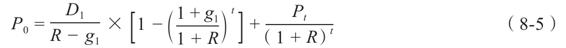
表達式中的第1項就是我們在第6章中討論過的增長年金的現值。在第1階段，增長率g₁可以比貼現率R大。第2部分是t時點的股票價格的現值，而第2階段從時點t開始。

我們可以計算t時點的股票價格P_t如下

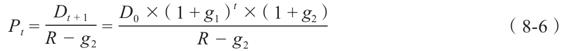
在這個計算中，我們需要利用t+1時點的股利D_t+1以得到t時點的股票價格P_t。注意，為了得到t+1時點的股利，我們使現在的股利D₀按照g₁的增長率增長了t期，然後再按g₂的增長率增長了1期。而且，第二階段的增長率g₂必須小於貼現率R。

【例8-5】兩階段增長模型

Highfield公司的股利預期會在接下來的5年裡以20%的增長率增長。隨後，預期增長率會一直穩定在4%。如果必要報酬率為10%，那麼股票的價值是多少？公司剛剛支付的股利為2美元。

這裡有大量的計算，但是它們主要是計算器的輸入輸出。我們可以首先計算5年後的股票價格P₅

然後我們將這個結果代入兩階段增長的公式，得到今天的價格

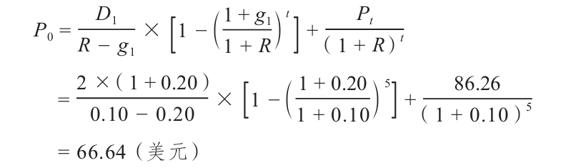
注意，這裡我們已知D₀=2美元，因此我們只需使股利按照20%的增長率增長1期就可以得到D₁。還要注意的是，本例中的g1大於R，但是這沒有關係。

8.1.3　必要報酬率的構成要素

到目前為止，我們把必要報酬率，也就是貼現率R看作已知的。我們將會在第12章和第13章對這個問題進行詳細討論。現在，我們希望探究股利增長模型中的必要報酬率的含義。在這之前，我們知道P₀為

P₀=D₁/（R-g）

我們重新整理這個式子來求得R

R-g=D₁/P₀

R=D₁/P₀+g　（8-7）

這就告訴我們總報酬率R包含兩個部分。第一部分D₁/P₀，叫作股利收益率（dividend yield）。因為這是由預期的現金股利除以現在的股價得到的，因此，在概念上它類似於債券的當期收益率。

第二部分是增長率g。我們知道，股利增長率也是股價增長率（見例8-3），因此，這個增長率可以理解為資本利得收益率（capital gains yield），也就是投資價值的增長速度。^[2]

為了說明必要報酬率的組成部分，假設一隻股票以每股20美元的價格出售。下一期的股利將是每股1美元。你認為這個股利會以每年10%的增長率無限期地穩定增長。如果你的預測是正確的，那麼，這隻股票的報酬率是多少呢？

根據股利增長模型，總報酬計算如下

R=股利收益率+資本利得收益率

=D₁/P₀+g

在這個例子中，總報酬率為

R=1/20+10%=5%+10%=15%

因此，這隻股票的期望報酬率為15%。

我們以15%為必要報酬率，計算1年後的股價P₁來驗證這個答案。根據股利增長模型，1年後的股價為

P₁=D₁×（1+g）/（R-g）=1×1.10/（0.15-0.10）

=1.10/0.05=22（美元）

請注意，這裡的22美元是20美元×1.1，因此，股票價格增長了10%，正好是應該增長的比率。如果你今天為這隻股票付出了20美元，年末時你將得到1美元的股利，此外還有22-20=2美元的利得。股利收益率為1/20=5%。資本利得收益率為2/20=10%。那麼，總報酬率為5%+10%=15%。

為了對書中一些確切的數據有一個感性的認識，根據2016年的《價值線投資調查》（Value Line Investment Survey），寶潔公司的股利在接下來的5年裡預期將以5%的增長率增長，其過去5年和過去10年的歷史股利增長率分別是7.5%和9.5%。在2017年，預計下一年的股利是2.85美元，而公司當時的股價是每股85美元。寶潔公司的投資者所要求的報酬率是多少？在這裡，股利收益率是3.35%，資本利得收益率是5%。因此，寶潔公司股票的總報酬率是8.35%。

8.1.4　乘數法估價

基於股利的股票估價方法面臨的一個最大問題就是很多公司並不派發股利。在這種情形下我們應該如何做呢？一個通用的方法就是使用我們在第3章中介紹過的一個指標——市盈率（PE ratio），定義為上一年每股價格除以上一年每股收益（EPS）。基於這種理念，會得到一些基準市盈率或者參考市盈率，我們要用這些市盈率乘以收益來得到價格

時點t的價格=P_t=基準市盈率×EPS_t　（8-8）

其中，基準市盈率可能出自一些不同的信息來源。它可能基於一些相似的公司（也許是行業平均值或中值），也可能基於一個公司自己的歷史水平。例如，假如我們正在嘗試為電動遊戲開發商Inactivision公司的股票估值，這家公司因其開發的“Slack Ops”系列遊戲而聞名。該公司並不支付股利，但是考察了它所處的行業之後，你認為20倍的市盈率對於這樣一家公司來說是適當的。最近4個季度加總的收益為每股2美元，所以你認為股票的售價應為20×2=40美元。如果股價低於40美元，那麼你就會認為它將是一個有吸引力的投資，而如果股價大於40美元，你就不會這麼認為了。

證券分析師在預測股票未來收益時花費了大量時間，特別是對下一年的預測。根據未來預期收益算出的市盈率叫作前向市盈率（forward PE ratio）。例如，如果該公司的一款大型在線角色扮演遊戲World of Slackcraft將更加流行，你可能認為Inactivision公司股票在下一年的收益將為每股2.5美元。在這個例子中，如果當前的股價是40美元，那麼前向市盈率就是40美元/2.5美元=16。

最後，應該注意的是，20倍的基準市盈率對應的是上一年的收益。如果下一年的每股收益為2.5美元，那麼下一年的股票價格將為20×2.5美元=50美元。用這類方式預測的股票價格被稱為目標價格（target price）。

通常，我們會對評估較新的公司感興趣，這些公司不支付股利並且也不盈利，這意味著收益是負數。此時我們應該怎麼辦呢？一個答案就是使用我們在第3章中介紹過的市銷率。顧名思義，這個比率是用每股市價除以每股銷售額。使用這個比率的方法類似於使用市盈率的方法，只是用市銷率代替了市盈率。就像市盈率一樣，市銷率也隨著產業和公司的成立年限變化而變化。典型的市銷率是在0.8～2這個範圍內，但是對於年輕的、增長較快的公司，這個值會大一些。

我們關於股票估價方法的討論歸納為表8-1，以便以後參考。

表8-1　股票估價概要

概念問題

8.1a　普通股估價時的相關現金流量有哪些？

8.1b　股票的價值是否取決於你期望持有時間的長短？

8.1c　當股利以固定的比率增長時，怎樣計算股票的價值？

[1] 關於股票價格，我們所做的唯一假設是，無論向前遞推多遠，它都是一個有限的數值。它可能十分大，但不是一個無窮大的值，因為沒有人曾經見過一個無窮大的股票價格，因此這個假設看起來是合理的。

[2] 在這裡和其他地方，我們對“資本利得”（capital gains）這個術語的使用並不太嚴謹。為準確起見，嚴格地講，資本利得（損失）應符合美國國稅局的定義。就我們的目的而言，使用術語“價格增值”（price appreciation）代替“資本利得”可能更為確切（但是不常用）。