e1 Stephen Ross 公司理財 v12A
5.1 終值和複利
我們首先來學習終值。終值(future value,FV)是指,在一定利率水平下,一筆金額在投資一段時期後將會增長到的數額。換句話來說,終值是指一筆投資在未來某個時點的現金價值。我們將會從最簡單的情況——單期投資開始討論。
5.1.1 單期投資
假設你存100美元於一個年利率為10%的儲蓄賬戶。1年之後你會有多少錢呢?你將會有110美元。這110美元相當於你的初始成本100美元同10美元利息之和。我們說這110美元就是100美元在利率為10%的情況下投資1年得到的終值,簡單來講,在利率為10%的情況下,今天的100美元相當於1年後的110美元。
總的來說,如果你的單期投資回報率為r,你的每1美元投資將會收回1+r美元。在我們的例子中,r等於10%,所以你的每1美元投資將會收回1+0.1=1.1美元。在這個例子中,你的投資是100美元,因而你投資的最終價值為100×1.1=110美元。
5.1.2 多期投資
回到我們投資100美元的例子中,在利率不變的情況下,2年後你將會有多少錢?如果你將110美元全部存入銀行,在第2年你將會得到110×0.1=11美元的利息,所以,你總共將會得到110+11=121美元。這121美元就是在利率為10%的情況下,100美元在2年後的終值。你也可以把這個問題看成,在利率為10%的水平下,現在投資110美元1年後的終值。這將變為一個單期投資的問題,所以你的每1美元最後將變成1.1美元,或者說110×1.1=121美元。
這121美元分為4個部分:第1部分是100美元的初始本金;第2部分是你第1年獲得的10美元利息;第3部分是你第2年獲得的10美元利息,前3部分加總共為120美元;最後的1美元(第4部分)是你第1年獲得的10美元利息在第2年再投資賺取的利息:10×10%=1美元。
把本金和累計的利息繼續留在投資中超過1期,從而對利息進行了再投資的這個過程叫作重複生息(compounding)。重複生息意味著賺取利上利(interest on interest),因而我們把這部分利息稱為複利(compound interest)。如果是單利(simple interest)的情況,利息就不會進行再投資,因此每期只賺取初始本金的利息。
【例5-1】利上利
假設你投了325美元在一個年利率為14%、期限為2年的投資上,2年後你將會得到多少錢?其中多少源於單利?多少源於複利?
在第1年年末,你將會獲得325×(1+0.14)=370.50美元。如果你將全部資金再投資從而賺取複利,那麼第2年年末你將會獲得370.50×1.14=422.37美元。你總共獲得的利息為422.37-325=97.37美元。在單利情況下你的初始本金每年賺得325×0.14=45.50美元利息,2年一共賺得91美元單利。剩下的97.37-91=6.37美元源於複利。你可以就此檢查一下,注意第1年賺取的利息是45.50美元。根據我們的計算,第2年的利上利因此為45.50×0.14=6.37美元。
讓我們更仔細地看一下之前所得到的終值121美元。我們將110美元乘以1.1得到121美元。這110美元是用100美元也乘以1.1後得到的。換句話說
121=110×1.1=(100×1.1)×1.1=100×1.1×1.1
=100×1.12=100×1.21
接下來的問題在於:3年後我們的100美元將會變為多少錢?在利率水平為10%的情況下,在第2年後,我們再一次投資121美元。我們每投資1美元將會收到1.1美元,或者說,121×1.1=133.10美元。因此,這133.10美元是
133.10=121×1.1=(110×1.1)×1.1=(100×1.1)×1.1×1.1
=100×(1.1×1.1×1.1)=100×1.13=100×1.331
你或許已經注意到這些計算的模式了,所以現在我們不妨進一步說明一下一般結論。我們的例子說明,將每1美元投於利率為r,期限為t的投資的終值為
終值=1×(1+r)t (5-1)
公式中的(1+r)t通常叫作1美元投資在利率為r,投資期為t時的終值係數,可以縮寫為FVIF(r,t)。
在我們的例子中,你的100美元在5年後將會價值多少呢?我們可以首先計算出相關的終值係數
(1+r)t=(1+0.10)5=1.15=1.610 5
你的100美元因此將會變為
100×1.610 5=161.05(美元)
表5-1列示了100美元的逐年增長情況。如表所示,每年賺取的利息等於年初金額乘以10%的利率。
表5-1 在10%利率水平下100美元的終值 (單位:美元)
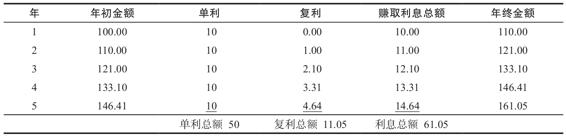
在表5-1中,你獲得利息總額是61.05美元。在5年的投資期中,你每年獲得的單利為100×0.10=10美元,由此你累積了50美元。另外的11.05美元得自複利。
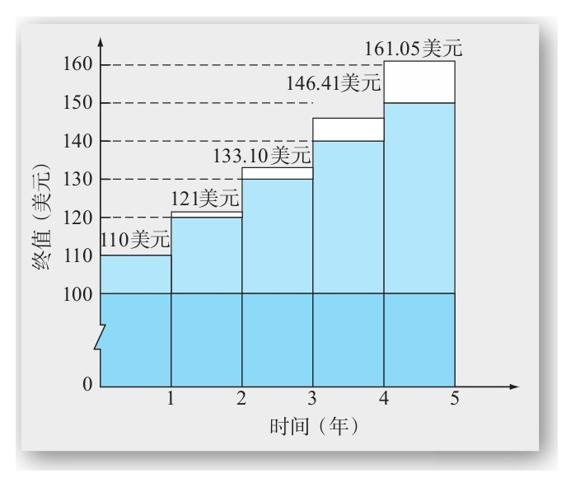
圖5-1 終值(單利和複利)
注:在利率為10%的水平下,100美元本金的增長情況。淺色區域表示單利,白色區域表示複利。
圖5-1說明了表5-1中複利增長的情況。注意每年的單利都是固定的,但是複利逐年增長。複利持續增長的原因是越來越多的利息參與了計息。
終值,尤其是長期投資的終值同假定的利率密切相關。圖5-2通過展示在不同利率下以及不同期間內1美元的增長情況而說明了這種關係。注意在20%的利率水平下,1美元在10年後的終值為6.2美元,但是在10%的利率水平下,1美元在10年後的終值僅為2.6美元。在本例中,利率翻倍對終值的影響將不僅僅是使之翻倍而已。
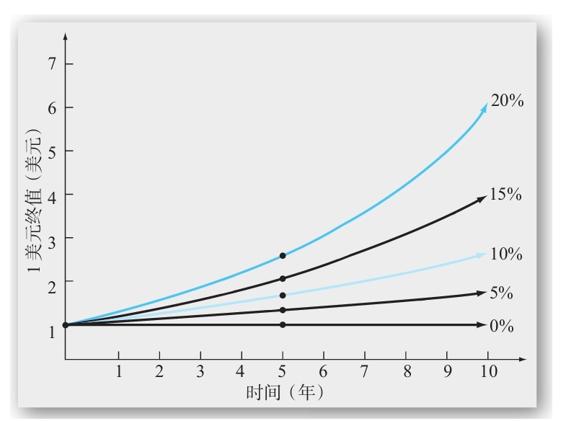
圖5-2 不同期限和利率下的1美元投資終值
為求終值,我們首先要計算相關的終值係數。有很多種方法可以計算終值係數。本例中,計算1.1的5次方還算容易,但如果是30年的投資,這種方法的工作量就太大了。
幸運的是,我們有一些簡便的方法求終值係數。大多數計算器中都有yx功能。你只需鍵入1.1,然後按yx鍵,再鍵入5,最後按“=”鍵就可以得出結果。這是一個簡單而準確的計算終值的方法。
另一種你可以嘗試的方法是使用涵蓋常見利率和期數的終值係數表。表5-2列示了一些這樣的係數。書後附錄中的表A-1列示了更多的終值係數。使用該表的時候,先找到10%利率對應的那一列,然後向下找到第5期對應的那一行,你就會見到我們之前計算出來的係數,1.610 5。
由於計算器不再像以前那麼昂貴,而圖表可以提供的數據太少,像表5-2這樣的終值係數表已經不像以前用得那麼多了。利率的報價通常到小數點後的3~4位,因此能達到這種精度的表將會非常龐大。鑑於以上原因,現實生活中人們逐漸不再使用圖表。在這一章中我們強調計算器的使用。
表5-2 終值利率係數
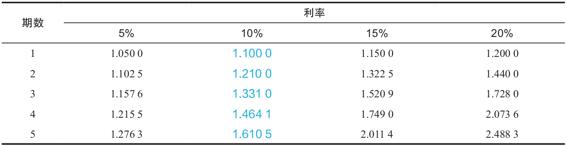
不過圖表依然有一些用處。為了確定計算過程是準確的,你可以從圖表中選擇一個係數,試著計算看能否得到一樣的結果。圖表中有大量的係數可供你選擇。
【例5-2】複利
你選定了一項回報率為12%的投資。這個投資回報率對你來說很不錯,因而你投資了400美元。3年之後你將會有多少錢?那麼7年之後呢?在第7年年末,你累計收到多少利息?有多少利息源自於複利?
根據我們的討論,利率為12%,期限為3年的終值係數計算如下
(1+r)t=1.123=1.404 9
你的400美元將會變為
400×1.404 9=561.97(美元)
7年後,你將會擁有
400×1.127=400×2.210 7=884.27(美元)
因此,你的400美元在7年間增長了不止一倍。
由於你的初始投資為400美元,884.27美元的終值中涵蓋的利息為:884.27-400=484.27美元。在12%的利率水平下,你的400美元初始投資每年獲得單利400×0.12=48美元。7年中,單利的總額為48×7=336美元。另外的484.27-336=148.27美元源自複利。
在短期內,複利的影響並不顯著。但是隨著期限的增長,複利的影響將會越來越大。一個極端的例子是,假設200年前,你的一位節儉的祖先在6%的利率水平下投資了5美元,你今天將會收到多少錢?終值係數1.06200=115 125.90(你在終值係數表中不會找到這個係數),所以你會收到5×115 125.90=575 629.52美元。請注意,如果僅以單利計算,你每年將會收到5×0.06=0.30美元。200年後,總數為60美元。其餘的均來自於利息的再投資。這就是複利的力量!
【例5-3】那個島值多少錢
為了進一步說明在期限很長的情況下複利的影響力,讓我們來看一個有關Perter Minuit和印第安人的例子。在1626年,Minuit以24美元和一些貨物買下了整個曼哈頓島。這個價錢聽起來很便宜,但是印第安人可能賺大錢了。這個原因是,假設印第安人將貨物賣出,並且將以10%的年利率投資24美元。今天這筆投資將會價值多少錢呢?
這筆交易已經完成391年了。在10%的利率水平下,24美元的投資已經變成很巨大的一筆錢了。那會是多少呢?終值係數是
(1+r)t=1.1391=15 295 000 000 000 000
即,15 295後面加上12個0。因而終值變為24×15.295=367,即367 000萬億美元。
顯而易見,367 000萬億美元是一筆很大的錢。有多大呢?如果你有這筆錢,你可以買下整個美國。整個美國!用現金。剩下的錢你可以買下加拿大、墨西哥或世界上的其他國家。
當然,這個例子有些誇張。在1626年,你很難找到一個回報率為10%,期限為391年而且失敗率為0的投資項目。
計算器使用說明 使用金融計算器
儘管到目前為止我們討論了很多種計算終值的方法,你們中的大部分還是選擇使用計算器完成計算。如果你正打算使用計算器計算終值,需要閱讀以下提示,如果不打算使用計算器,跳過這段提示。
金融計算器是在普通的計算機基礎上添加一些附加功能。特別值得一提的是,它預先設定了一些金融公式,因此它可以直接計算出像終值這樣的參數。
金融計算器的優點是可以幫你省去很多計算步驟。但另一方面,需要明確金融計算器只是幫你做了一些數字上的處理,你依然需要了解計算過程。實際上,就像老笑話說的那樣:任何人都可能犯和貨幣時間價值有關的錯誤,但使用金融計算器的人需要的是上緊螺絲!我們在這一部分有兩個目標:首先,教會你計算終值;之後,教會你避開金融計算器初學者經常犯的錯誤。
如何使用金融計算器計算終值
在一個典型的金融計算器上你將會看到如下5個按鍵,它們一般看起來像這樣:

我們首先要注意其中的4個按鍵。按鍵PV和FV的含義和你想的一樣:現值和終值。按鍵N指期數,它的含義和我們經常用的t一樣。按鍵I/Y指利率,它的含義和r一樣。
如果我們的使用方法正確(見下一章),那麼計算終值將會非常簡單。回到我們之前的問題:求100美元在利率為10%的情況下5年後的終值。我們之前得出的結論為161.05美元。實際的精度將會由於你使用的計算器的不同而有所差異。使用金融計算器你需要進行如下步驟。
(1)鍵入-100。按PV鍵。(鍵入負值的原因,下一部分將介紹。)
(2)鍵入10。按I/Y鍵。(注意鍵入的是10而不是0.1。下一部分將介紹原因。)
(3)鍵入5。按N鍵。
現在我們已經鍵入了所有相關信息。想求終值,我們需要問金融計算器FV的值是多少。由於金融計算器的不同,你需要按CPT之後再按FV,或者直接按FV。無論你是用哪種方法,你最終都會得到161.05。如果你沒有得到這個結果(一般是由於初次使用金融計算器),我們接下來將會為你提供一些幫助。
在解釋你可能犯的錯誤之前,我們先介紹一個標準的使用形式以便你使用金融計算器。還是用剛剛的例子,我們將會這樣解決這個問題:

重要提示:附錄D介紹了更多常用的金融計算器使用方法。需要的時候你可以查閱。如果附錄D也沒有介紹你需要計算的變量,你可以選擇閱讀計算器使用說明書。
為何使用金融計算器得到了錯誤的答案
很多原因會導致你使用金融計算器得出錯誤答案。在這一部分,我們將會告訴你什麼可以做,什麼不可以做。如果你不明白為何會出錯,則需要重新閱讀這一部分。
我們需要檢查2種類型的事情:有3件事情你只需要做一次,有3件事情你每次計算的時候都需要做。3件你只需要做一次的事情是:
(1)確保你的金融計算器處於可以顯示小數點後多位的狀態。很多金融計算器只顯示小數點後兩位。這經常會為我們帶來麻煩,因為我們常常要計算像利率這樣數值很小的數。
(2)確保你的計算器假設一年只支付一期。很多金融計算器默認一年支付12期。
(3)確保你的計算器處於“結束”模式。這一般來講不是問題,但有時你會不小心將計算器調到“開始”模式。
如果你不知道怎樣設置以上3件事情,你可以參考附錄D或者計算器說明書。另外,有3件事情是你每次計算時都需要做的:
(1)在開始之前,清空計算器。這很重要,如果不這樣做的話,你會得到錯誤的結果。必須養成每次計算之前清空計算器的習慣。怎樣清空計算器因計算器的不同而不同。你可以參考附錄D。你需要做的不僅僅是清空計算器。比如說,使用BA II Plus型號的計算器時,你在計算貨幣時間價值之前,需要先按2nd再按CLRTVM來清空之前的數據。使用任何一個計算器你都需要這要做,學會它!
注意在你不用計算器的時候將它關閉並將蓋子合上。哪怕在關機後,很多金融計算器仍會記住你鍵入的任何東西。換句話說,除非你將它清空,否則它會記住你所有的錯誤。同時,如果你在計算過程中出現了錯誤,你需要清空數據,重新開始。保險一點總比出錯好。
(2)計算現金流量時鍵入一個負值。大多數金融計算器要求你輸入現金流出時鍵入負值,輸入現金流入時輸入正值。換句話說,這經常意味著你需要在鍵入現值時加上一個負號(這是因為現值代表你為了以後的收入而在今天放棄的現金數量)。所以說,在你求現金現值的時候,你不應該為得出一個負數而感到驚訝。
(3)正確鍵入利率。金融計算器默認利率以百分比的形式表示。因此如果利率為0.08(8%),你需要鍵入8而不是0.08。
如果你參照以上指導計算(尤其是清空計算器這一條),使用金融計算器解決下一章的問題對你來說應該沒有問題。我們將會在合適的時候提供更多有關金融計算器的指導。
5.1.3 關於複利增長的說明
如果你考慮將錢投入一個計息賬戶中,在不將錢提出來的情況下,該賬戶的利率就是你的錢的增長率。如果利率為10%,簡單地說你每年的錢都會比上一年多10%。在這種情況下,利率就是一種複利增長率。
這種計算終值的方法非常普遍,你可以使用它來計算其他有關增長率的問題。比如說,你的公司目前有10 000位僱員,你估計每年的新增僱員率為3%。5年之後你將會有多少僱員?在這裡,我們用10 000人代替金額,使用僱員增長率來代替利率,計算過程是一樣的
10 000×1.035=10 000×1.159 3=11 593(人)
在未來的5年你將會有1 593名新僱員。
再看另一個例子。根據調查,沃爾瑪2016年的銷售收入為4 810億美元。假設銷售收入的年增長率為15%。如果這個假設準確的話,那麼2021年沃爾瑪的銷售收入為多少?你自己可以驗算一下,這個數字大約為9 680億美元,也就是兩倍多一些。
【例5-4】股利增長
TICO公司目前的股利為每股5美元。你認為股利將在之後無限的年度裡每年增長4%。8年後股利將為多少?
這裡的現金股利增長是一個管理層的決策問題,但是計算過程是一樣的
終值=5×1.048=5×1.368 6=6.84(美元)
在這期間股利將會增長1.84美元。我們將會在之後的章節討論股利增長的問題。
概念問題
5.1a 投資終值的概念是什麼?
5.1b 複利的概念是什麼?複利和單利的區別是什麼?
5.1c 在利率為r的情況下,1美元投資t期之後的終值是多少?