附錄C　財務分析

本附錄將介紹運營管理中涉及的財務分析的基本概念和工具，包括成本的種類（固定成本、可變成本、沉沒成本、機會成本、可避免成本）、風險與期望值和折舊（直線法、年數總和法、餘額遞減法、雙倍餘額遞減法、業務量折舊法）。我們還將討論作業成本和資本成本的計算，主要關注的重點是資本投資決策的內容。

C.1　概念與定義

我們首先從幾個基本概念入手。

1.固定成本

固定成本是不隨產出多少變化的費用。事實上沒有絕對的固定成本，許多費用實際上只是在一定產出的範圍內保持不變。常見的例子有租金、財產稅、大多數折舊、保險金和高級管理人員的工資。

2.可變成本

可變成本是隨著產出的變動而變動的費用。舉例來說，美國鋼鐵公司每多生產一單位的鋼板要消耗一定數量的材料和勞動力，而多消耗的材料和勞動力所增加的費用可以進行分割而分別分配到增加的每單位鋼板上。許多企業的經常費用也是可變的，因為水電費和維修費等也是隨著生產水平的變動而變化的。

圖C-1　總成本中的固定成本與可變成本

圖C-1說明了總成本是由固定成本和變動成本組成的。注意由於固定成本是不變的，因而總成本的增長率和可變成本增長率相等。

3.沉沒成本

沉沒成本是過去已經發生的費用或沒有殘值的投資，因此在進行投資決策時不必把它考慮進去。沉沒成本也可能在本質上是固定成本的當前成本，如建築物租金。例如，假設一家生產冰激凌的工廠租用了一間廠房，並考慮在這個廠房中生產冰凍果子露。如果公司生產冰凍果子露，成本會計將分攤一部分房租到冰凍果子露的成本中，但事實上這筆房租是不變的，決策時不用把這筆費用作為相關費用考慮。租金是“沉沒”的，它已經存在，不論如何決策，這一費用都是不變的。

4.機會成本

機會成本是由於在決策時沒有選擇最優方案而失去的利益或者優勢。假設一家公司要投資100 000美元，有兩個可比方案可供選擇，A投資方案可以獲得淨利潤25 000美元，B投資方案可以獲得淨利潤23 000美元。A方案明顯是一個好的選擇，因為有25 000美元回報。如果決策時採用了B方案，那麼B方案的機會成本就是所損失的2 000美元的利潤。

5.可避免成本

如果進行了某項投資，某項費用就不會產生，但是如果不進行投資，就一定會出現某項費用，這種費用就是可避免成本。假設某公司有一臺機床，該機床出現了故障。由於該機床是公司作業所必需的，所以機床必須修理或者更新。如果購買新機床，那麼維修成本就是可避免成本。可避免成本能降低新投資成本，是因為投資的發生使可避免成本不會發生。可避免成本是通過花錢來省錢的例證。

6.期望值

任何投資都有風險，因為將來的情況很難絕對準確地被預測到。一些數學方法如期望值法有助於研究這種不確定性。期望值等於期望結果乘以實現期望結果的概率。如前例，方案A的期望收入是25 000美元，方案B則為23 000美元。假設方案A的實現概率是80%，方案B是90%，那麼期望值計算如下：

期望值=期望結果×實際結果等於期望結果的概率

方案A：25 000×80%=20 000（美元）

方案B：23 000×90%=20 700（美元）

看起來方案B是一個較好的選擇，其期望值超過方案A的700美元。

7.經濟壽命與報廢

當企業投資購買生產設備時，要估計設備的使用壽命。從會計角度考慮，這臺設備應在這段時間內折舊完畢。假如該設備在這一段時期發揮功能，就會陳舊或磨損，並且需要更新設備，但這種預計的使用壽命一般和實際並不一致。

假設一臺設備購入時估計其使用壽命是10年。在這10年中的某一時間開發出了一種新設備，它比原來的機器效率更高或更經濟，這時舊機器就過時了，而與該機器是否損壞無關。

機器的經濟壽命是指機器能提供最好的方法來完成任務的時間段。當更先進的方法被研製出來的時候，舊機器就被淘汰了。這時，機器的賬面價值就失去了意義。

8.折舊

折舊是分攤設備資本成本的一種方法。在使用和消耗過程中，任何資本性資產，包括房屋、機器等的價值都會隨使用時間的推移逐漸減少。攤銷和折舊這兩種方法通常可以相互替代。按傳統的說法，折舊是根據有形資產的物理或功能的消耗分攤成本，如房屋或設備。攤銷是把無形資產在有效期限內分攤到成本中，如專利權、租借權、特許經營權和商譽等。

折舊不能在其生命週期的任何時點反映資產的真實價值，由於任何時候都可能發生舊機器過時淘汰的情況，設備實際價值與賬面價值之間往往存在較大的差異。同時，由於折舊率的大小對稅收影響很大，企業在選擇折舊方法的時候往往首先考慮折舊方法對稅收的影響，而不是賬面價值對實際變現價值的反映能力。

下面我們將介紹五種常用的折舊方法。

直線法

使用這種方法，設備的價值在使用壽命期內每年以相同的量遞減。一般公式為：

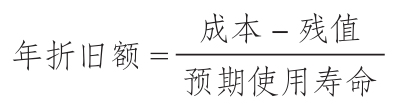
假設一臺機器原值10 000美元，估計殘值為0，使用壽命為10年，其年折舊額為1 000美元，10年內全部折完。如果10年後的殘值為1 000美元，則年折舊額為：

年數總和法

年總和法（sum-of-the-years’-digits，SYD）的目的是在使用壽命的早期提取較高的折舊費，減少賬面價值，而在使用壽命的後期以較低的折舊率折舊。

假設估計使用壽命是5年，總折舊分數累計為：1+2+3+4+5=15。第一年折舊率為5/15，第二年為4/15，依此類推，最後一年是1/15。

餘額遞減法

這也是加速折舊的一種方法。每年用固定的折舊率乘以每年的賬面價值餘額，這個折舊率使資產在結束時，賬面價值恰好是它的殘值。在任何情況下，資產的價值最終不能低於它的殘值。使用餘額遞減折舊法時，折舊率的允許範圍一般由內部收入服務條例控制。下面以下表簡要說明前面的例子，表中40%的折舊率是任選的。注意，這一折舊是基於資產的原值，沒有扣除資產的殘值。

在第5年，按40%減少賬面價值將會使資產低於殘值。因此，只需再折舊203美元就可使賬面價值等於殘值。

雙倍餘額遞減法

雙倍餘額遞減法是在資產壽命的早期提取較高折舊費的一種方法，它在稅金方面更為有利。這種方法用直線法折舊率的兩倍來提取折舊費，本質上和直線折舊法是一樣的。如果有10年壽命期的設備年折舊率為10%，那麼雙倍餘額折舊法的年折舊率為20%。

業務量折舊法

這一方法的目的是把資產的投資額按其使用的比例分攤到成本中。這種方法適用於那些重複同樣操作的機器。這一機器的壽命不是以年計量的，而是以預計其在報廢前可進行的作業總數來估算。假設一臺金屬衝壓機壽命是衝壓100萬次，設備價值是100 000美元。每衝壓一次計提折舊費為100 000÷1 000 000，即0.1美元。假設殘值為0，歷年折舊情況如下表所示。

該折舊法試圖按實際的使用情況提取折舊費用，能更精確地匹配生產產出。而且，由於機器的變現價值與它的剩餘使用壽命相關，賬面價值與變現價值是可能一致的。令人擔憂的是，技術發展迅速，常常使機器提前被淘汰。在這種情況下，賬面價值就不能反映真實價值。

C.2　作業成本法

為了知道某一產品或提供某項服務佔用了多少成本，必須應用某些方法將製造費用分配到生產活動中。傳統的方法是根據直接人工成本或工時將經常費用分配計入成本。將經常費用的總量除以總直接勞動力工時可以得到經常費用比例。該方法所遇到的問題是，在過去10年中直接人工成本佔總成本的百分比急劇下降。例如，先進製造技術以及其他改進生產的技術引入使許多工作中的直接人工成本已經降到總製造成本的7%～10%。因此，許多高度自動化的工廠就出現經常費用高達600%甚至1 000%的情況。

傳統的會計方法是按直接人工分配經常費用，這種會計方法常常會導致一些問題。例如，根據計劃成本的比較，我們可能會選擇自動化生產而捨棄勞動密集型生產。不幸的是，安裝設備時製造費用並不會消失，而如果採用勞動密集型生產，總成本實際上可能會更低。這種方法也可能會因為投入過多的時間去追蹤直接人工時間長度而浪費投入的精力。例如，一家工廠花費了65%的計算機成本去追蹤有關直接人工時間的信息，儘管直接人工費用僅佔總生產成本的4%。

作業成本法 （activity-based costing）通過簡化經常費用的分配過程，更直接地反映生產活動中發生的經常費用所佔的實際比例來解決這些問題。原因因素常被稱為成本動因，被識別出來作為分配經常費用的依據。這些因素可能包括機器時間、佔地面積、計算機時間、空運時間或運輸里程。當然，經常費用分配的精度取決於成本動因的選擇是否恰當。

作業成本法包含兩階段分配過程。第一階段是將經常費用分配到成本活動庫（cost activity pools）。這些庫中包括諸如機器準備、發佈購貨訂單、檢驗零部件之類的活動。第二階段根據完成任務所需的成本庫活動的數量，將成本庫的成本分配給這些活動。圖C-2展示的是傳統成本法與作業成本法的比較。

圖C-2　傳統成本法與作業成本法

思考表C-1作業成本法的例子。兩種產品A和B使用同樣數量的直接人工工時，相同時間的直接勞動力可生產5 000單位A產品或者20 000單位B產品。應用傳統成本法，每種產品將分攤同樣數量的製造費用；應用作業成本法，成本將被分配給特定的活動。因為每種產品需要不同數量的處理時間，因此從成本庫中為這些產品分配不同數量的經常費用。

表C-1　用作業法分配經常費用

資料來源：R.Garrison，Managerial Accounting，12th ed.（New York：MCGraw-Hill，2007）.

如前所述，作業成本法為每一項活動或事項建立起可以看成成本動因的成本庫，並根據完成產品或作業所需的獨立活動數量，將經常費用分配給產品或作業，這種方法克服了成本扭曲的問題。因此在前面的情況下，低產量的產品分配的成本往往較高，包括設備調整、購貨訂單及質量檢驗，因此對於其他產品而言，單位成本較高。

作業成本法有時被稱為業務成本法。這種方法較之其他成本法，提高了經常費用的可追溯性，也為管理者提供了更加精確的單位成本數據。

C.3　稅收的影響

稅率以及使用稅率的方法偶爾也會變化。當分析專家評論投資方案時，稅金常被認為是決定性因素，因為折舊費用直接影響應納稅的收入，因而影響利潤。在開始的幾年中，加速提取折舊為投資提供了一個額外的資金來源。1986年以前，公司可利用投資減稅，使稅收責任直接減少。後來稅法發生了變化，因此，遵守當前的稅法，並嘗試預測可能影響當前投資和會計活動的未來變化變得十分關鍵。

C.4　選擇投資方案

資本投資決策已經變得高度理性化了，解決該問題具有多種可用的技術足以說明這一點。與定價策略及市場決策對比，決策者往往對資產投資決策更具信心，因為影響投資決策的變量相對而言更易獲取，並且可以量化到一定精度。

投資決策通常可分為6種：

（1）購買新設備或設施。

（2）現有設備或設施的更新。

（3）自制或外購決策。

（4）租賃或購買決策。

（5）工廠臨時停工或永久關閉決策。

（6）增加或減少產品或產品系列。

投資決策是根據可接受的投資回報率底限來制定的。作為問題的出發點，可接受投資回報率底限可以認為是投資金額的資本成本。當然如果不能收回資本成本，投資活動肯定不會發生。

投資方案通常根據其產生的超過資本成本的收益大小進行排序。根據這一辦法，只有有限投資基金的企業可以選擇可產生最大淨收益的投資方案（淨收益是指投資獲得的毛利益減去投資融資成本後的收益）。通常，如果收益不能超過投資資本的邊際成本，這項投資就不能進行（投資資本的邊際成本是指沒從外部渠道融資一單位新增資本所需的成本）。

1.確定資本成本

資本成本是通過對負債和權益籌資成本的加權平均計算得到的。該加權平均值將隨企業所採用的融資策略的不同而不同。最常用的融資渠道是短期負債、長期負債和權益性融資。銀行貸款是短期負債，債券一般是長期負債，股票是權益性融資的常見形式。下面，對於每種融資形式我們都給出一個簡短的例子，然後說明如何綜合這幾種融資形式確定資本成本的加權平均值。

短期負債成本取決於貸款利率以及貸款是不是減息貸款。記住利息對公司具有稅收抵減的作用。

如果銀行貸款為減息貸款，則貸款面值扣除利息後才是企業實際可用的資金額。當需要保留補償性餘額時（即將貸款面值的一定百分比保留在銀行中作為抵押），企業實際可用的資金也將減少。在這兩種情況下，貸款的有效利率或實際利率都高於其名義利率，因為從貸款中獲得的資金少於貸款金額（面值）。

短期負債舉例

假設某公司貸款150 000美元，期限為1年，利率為13%，該貸款為減息貸款，並且要求保留10%的補償性餘額，則有效利率的計算如下：

可用資金額如下所示（單位：美元）。

注意：貸款的有效成本顯著高於貸款的名義利率。

長期負債通常通過出售公司債券的方式獲得，債券的實際成本可以通過計算兩種類型的收益來獲取：簡單（票面）收益及到期收益（有效利率）。第一種收益涉及的是一種簡單的近似值，第二種則要精確得多。名義利率等於按債券面值（到期值）支付的利率，通常按年計算。債券通常以1 000美元的票面價值發行，發行價可能高於面值（溢價發行）或低於面值（折價發行，又稱為原始發行折扣）。當發售利率低於市場現行利率時，債券以折價發行。在這種情況下，其收益就會高於名義利率。債券以溢價發行時的情況與折價相反。

債券的發行價格等於票面價值（或面值）乘以溢價（或折價）比率。

長期負債舉例

假設公司發行10年期400 000美元的債券，利率為12%，以97%的價格折價發行。收益計算如下：

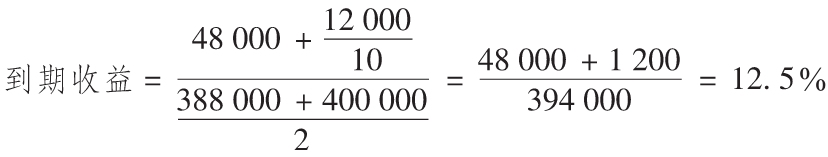
注意，債券以折價發行，因此收益超過名義利率（12%），債券利率對公司而言是減稅因素。

權益性籌資（股票）的實際成本以股利的形式表現，對公司來講股利不是減稅因素。

其中每股價值等於每股的市場價格-浮動成本（即發行股票的成本，例如經紀人佣金、印刷成本等）。應該注意這一價值沒有考慮投資者對市場價格上升的期望。該期望是基於對每股盈利的期望增長以及由於購買股票所帶來的相關風險。資本資產定價模型（CAPM）可用於分析這種影響。

普通股成本舉例

假設某公司發行了一種股票，每股股息為10美元，每股淨值為70美元，股息增長率為5%。

為了計算加權平均資本成本，我們先要考慮每種融資渠道籌集的資金佔總資金的百分比，然後計算每種融資方法的稅後成本，最後根據其使用金額為每種成本賦予相應的權重。

計算加權平均資本成本舉例

假設某公司的財務報表中顯示瞭如下的數據。

在我們的例子中，假定以上每個百分比表示該項資本的成本。此外，我們還需要考慮公司適用的稅率，因為債券及短期借款利息都可以抵稅。假設公司適用的稅率為40%。

在展開本節內容的過程中，我們在計算上做了很多假設。這些方法應用於某一特定公司時，其中的很多假設會有變化，但基本概念是一樣的，並且記住：我們的目標是簡化稅後資本成本的計算。在通常情況下只需要計算特定項目的資本成本，而我們展示的是計算整個企業的資本成本的實例。

2.利率的影響

有兩種方法可以解釋累計利息的影響：一種是將整個時段中產生的總量折算到未來某一時點，記為複利值；另一種就是將各個未來時點的金額扣除利息折成現值。

3.單筆金額的複利值

愛因斯坦曾將複利利息稱為世界第八大奇蹟。讀完本節的內容以後，我們可以看到經過很長一段時間後，複利利息會快速增長，你也許會希望能制定這樣一條新的政府政策：當孩子出生時，父母必須將1 000美元存入這個孩子的退休基金，當孩子65歲時可以兌現。這樣可以減輕社會保障的壓力和其他州政府及聯邦政府退休津貼的壓力。即使通貨膨脹使貨幣大大貶值，仍能保留一大部分錢。若投資回報率為14%，我們最初1 000美元的終值扣除通貨膨脹的損失4 500 000美元會得到5 000 000美元，也就是說比原來翻了500倍（許多中性基金的長期年收益率都超過14%）。

運用電子數據表和計算器進行這些計算都十分簡便。“應用電子數據表”的框中說明了最有用的財務功能，但仍有許多人藉助複利係數表來計算複利值。如利用附錄I中的表I-1（1美元的複利之和），我們可以看到在10%的利率下，1美元在3年後的複利終值為1.331美元，用該數字乘以10得到13.31美元。

4.年金的複利值

年金是指在數年間每年收取相同的金額。通常年金在每期期末收到，在當期不獲取利息。3年期的年金第一年年末投入10美元（如果在接下來兩年，這10美元持續投入其中，那麼就可獲得後兩年的利息），第二年年末投入10美元（這10美元可以在最後一年獲得利息），第三年年末投入10美元（沒有獲利的時間）。如果年金是投入到年利率為5%的儲蓄賬戶中，那麼年利率為5%的10美元年金3年的複利值為：

年金終值的一般計算公式為：

式中　Sn ——年金複利值；

　R——年金；

　N——以年為單位的期數。

用該公式解釋前例，可得：

在附錄I中，表I-2顯示，當利率為5%、年數為3時，1美元的年金終值係數是3.152。用該數乘以10美元得到31.52美元。

以我們前面談到的退休保障金投資為例，假設從21歲開始每年存入2 000美元，收益將會是多少？假設當前AAA級債券的收益率為9%，由附錄I表I-2可以得出，30年後（51歲時）這些投資的價值是2 000美元的136.3倍，將達到272 600美元。再過14年（在65歲那一年）這筆投資將價值963 044美元（需要使用計算器，因為表中只給出了30年的係數，假定2 000美元在每年年末存入），但又有哪個21歲的年輕人會想到退休以後的事呢？

5.未來單筆支付的現值

複利值用來確定資金在未來某一時點的價值，而現值（PV）的計算結果正好相反，它用於確定未來收入的總和或者多筆未來收入流入現在的價值。大部分投資決策都使用現值而非複利值，因為影響未來的決策是現在做出的，將未來的投資回報轉化為決策時刻的現值會更好一些。通過這種方式，就可以將各種投資議案用現值表示出來。

舉例來說明這個問題會更清楚一些。假如一位富有的叔叔打算送你一件價值100美元的禮物或者10年後送你一件價值250美元的禮物，你將做何選擇？你必須權衡10年後250美元的價值與現在100美元的價值，假定平均每年的通貨膨脹率為10%。把250美元折現，你可以比較其與現在100美元的購買力大小。通過求解複利值，可求得現值（P）。已知利率為10%，10年後的複利值（V）為250美元，其複利終值公式為：

兩邊同時除以（1+i）n ，得：

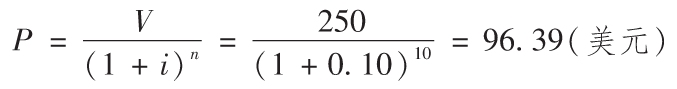
以上計算表明，在10%的通貨膨脹率下，10年後獲得250美元僅相當於現在獲得96.39美元，所以明智的選擇應該是現在的100美元。

在求解現值問題時，我們也經常利用複利係數表。藉助附錄I中的表I-3，10年後1美元的現值係數為0.386，乘以250美元，結果為96.50美元。

|專欄C-1|

運用電子數據表格

我們希望大家都能運用電子數據表格進行這些計算。儘管計算機簡化了這些運算，但大家還是應該瞭解計算機實際所做的工作。此外我們也應該對電子數據表格進行檢驗，確保公式設置正確。由於電子表格出錯帶來錯誤決策從而帶來慘痛結果的例子比比皆是。

為便於你快捷參考，我們給出下列最有用的財務公式。它們都是選自微軟Excel的幫助欄。

PV（rate，nper，pmt）：得出投資現值。現值是指一系列未來的支出現在價值的總額。例如，當你向某個人借貸時，對借出人來說，借款金額就是借貸額的現值。rate是指每期利息率。舉例來說，如果你獲得一筆汽車貸款，年利率為10%，每月支付一次，則月利率為10%/12，即0.83%。在公式中你可以設定rate為10%/12或者0.83%或者0.008 3。nper是指年金支付的總期數。例如，假設你獲得一筆4年期汽車貸款並按月償還，借貸期數是4×12（即48）。這時，你應該在公式中把nper設置為48。pmt是指每期支付的金額，它在整個償還期保持不變。一般來說，pmt包括本金和利息，但不包括其他費用和稅。例如，對於一筆10 000美元、利率為12%的4年期汽車貸款，月償還額為263.33美元，那麼就把公式中的pmt設置為263.33。

FV（rate，nper，pmt）：按期支付固定金額、固定利率的終值計算。rate是指每期利率。nper是指年金支付的總期數。pmt是指每期支付的金額，它在整個償還期中保持不變。通常pmt包括本金和利息，但不包括其他費用和稅。

NPV（rate，value1，value2，…）：基於一系列現金流和一個折現率計算投資淨現值。一項投資的淨現值是指一系列未來支出（負值）和收入（正值）的現值。rate是一個期間的折現率。value1，value2，…，應按時間順序依次列出，收入/支出均發生在期末。

IRR（values）：計算一系列用數值表示的現金流的內部收益率。現金流不必像年金一樣要求都相等。內部收益率是指一項投資取得的收益率，該項投資由定期發生的支出（負值）和收入（正值）構成。value是用來計算內部收益率的一個數組，或者是一系列單元格的引用，其中包含了計算內部收益率需要的數字，這些數字中至少包含一個正數和一個負數才能得出內部收益率。IRR用這些數字的順序來表示現金流的順序，因而當輸入這些支出和收入數值時，應確保它們的順序與你預期的相同。

資料來源：From Microsoft® Excel.Copyright©2016 Microsoft Corporation.

6.年金的現值

年金現值是指將在未來收到的年金值摺合到現在的值。要計算期數為3年、年金金額為100美元、利率為10%的年金現值，可以利用現值係數表將每年的年金折現，然後再求和。注意，年金是在每年年末收到的。

計算年金現值的一般公式為：

式中　An ——n年的年金現值；

　R——每期的收入；

　n——以年為單位的年金的期數。

利用該公式計算前例得：

附錄I的表I-4中包含了不同到期值年金的現值。當利率為10%、期數為3時，1美元年金的現值係數為2.487。我們的年金為100美元而不是1美元，與年金現值係數相乘，可得現值為248.70美元。

如果未來各年收到的年金不相等，則應將各年年金逐一折成現值再求和。雖然這樣比較煩瑣，但這些步驟是不可簡略的。

7.折現後的現金流

折現後的現金流是指未來產生的資產支付流摺合為現值的現金流。它是一種簡單的現值分析，包括一次支付、年金以及其他各種類型。

C.5　投資排序的方法

1.淨現值法

淨現值法是一種企業常用的方法。這種方法基於項目資金流入量的現值超過投資額的數量做決策。

一家公司正考慮兩個可供選擇的投資方案，兩個方案的投入量分別為30 000美元和50 000美元，未來各年的現金流入量如下表所示（單位：美元）。

我們要在A方案和B方案之間做出選擇，比較兩者中哪個項目的淨現值更高。假定資本成本為8%（單位：美元）。

由上表可見，方案A較好，因為它的淨現值比方案B多35美元（=9 930-9 895）。

2.投資回收期法

投資回收期是通過比較各方案收回投資時間的長短，並以此為依據進行方案排序的方法。該方法的基本原理是投資回收的越快，就能越早對其他收益項目進行再投資。這樣公司可以用投資基金獲得最大的收益。

考慮兩個投資方案，投資金額均為1 000美元。第一個方案在以後的6年中，每年收入200美元；第二個方案在前3年每年獲得收入300美元，後3年每年獲得收入100美元。

如果選擇第一個方案，則可以在第5年年末收回投資，而第二個方案在第4年年末收入總額就已達到1 000美元。這樣第二個方案用這1 000美元進行再投資的時間就要比第一個方案早一年。

雖然人們已經不經常只用投資回收期作為投資決策依據，但該方法經常與其他方法結合使用來說明收回全部投資的時間。投資回收期的主要不足是不考慮投資回收期以外的收入以及不考慮資本的時間價值。如果一種方法忽略了資本的時間價值，那麼這種方法是值得商榷的。

3.內部收益率法

內部收益率被定義為現金流入的現值與投資額相等時的利率。計算內部收益率沒有直接可用的程序或公式，一般使用插值法或者重複計算求得。

假設我們要計算某方案的內部回報率，該方案的投資金額是12 000美元，在以後4年中每年現金流入量為4 000美元。我們可以試算，現值係數為：

接下來我們就可以找出期數為4，現值係數為3.000的利率。因為3.000介於2.914和3.037之間，所以該利率必介於12%和14%之間（見附錄I表I-4的第4列），利用線性插值法可得：

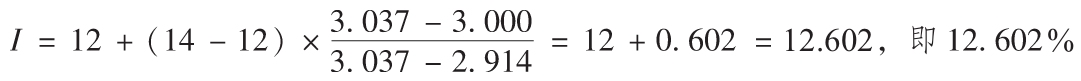
以上計算得出了內部收益率較好的近似值。

如果現金流入的折現率為12.6%，則現金流入的現值與投資金額大致相等。因此該方案的內部收益率為12.6%，可以將資本成本與內部收益率做比較以決定投資的淨收益率。在本例中，如果資本成本是8%，則該投資的淨收益率為4.6%。

淨現值法與內部收益率法的步驟在本質上是相同的。它們的區別是淨現值以收入超過投資的數量來比較投資方案，而內部收益率則用收益率進行比較。此外，內部收益率法偶爾也會遇到計算的問題，因為計算中出現了多種利率。

4.壽命不同的投資方案的評估

當各投資方案的壽命長度都相同時，可以運用上述方法計算，得出合理的各方案的相對價值，從而可以做出比較。然而，當壽命長度不相等時，如何聯繫不同的時間期間的問題就出現了。備選方案的壽命與原方案一致嗎？壽命相對短、較早被更新的設備，其生產率應該高一些嗎？未來設備的成本如何估計？

對在決策時不可預見的投資進行評估，估計值的準確度不可能很高。這些問題仍需要繼續探索，並且需要為評估提出合理的依據。

C.6　應用舉例：投資決策

例C-1　擴建決策

威廉·威爾遜陶瓷製品公司（William J.Wilson Ceramic Products，Inc.）租用設備生產耐火磚。由於需求增加，該公司可以投資購買新的設備，提高產量，增加銷量。產銷量增加，耐火磚的單價還是會保持10美元。在進行工藝分析與成本分析的基礎上，會計部門向經理提供了年增長量為100 000塊磚的情況下的成本估算（單位：美元）。

使用年數總和法折舊，稅率為40%。公司的策略是，如果投資報酬率低於20%，就不進行投資。那麼是否要實施擴建計劃呢？

解答

計算投資成本（美元）：

計算整個投資壽命週期的各年現金流量。

租賃費用是沉沒成本。不管是否進行投資，該成本總要產生，所以它與決策無關，不在考慮範圍之內。年生產成本包括水電費用、勞動力成本和原材料成本，這三者總額為6 000 000美元/年。

年銷售收入為：10×100 000=1 000 000（美元），折舊前稅前的年收入等於總收入（1 000 000美元）減去去年生產費用（600 000美元），等於400 000美元。

接著，利用年數總和法（年數總和=1+2+3+4+5=15），將折扣額從400 000美元的年收入中扣除。

當稅率為40%時，計算年現金流量。下面只給出第一年現金流入量的求解過程。

計算現金流量的現值。由於公司要求至少20%的投資回報率，則將各年現金流量乘以20%的現值係數即可。各年的現金流量各不相同，要分別運用各年的現值係數。

現在來觀察淨現值是正還是負。

當折現率為20%時，淨現值為正，這說明公司的投資報酬將超過20%，因此應實施該擴建計劃。

例C-2　更新決策

布魯維爾公司給瓶子貼標籤的機器已經使用5年了。該機器當年的購買價格是4 000美元，折舊時間為10年（用直線法折舊），殘值為0。若現在將該設備出售，可獲得2 000美元。公司可以購入一臺新標籤機，價格為6 000美元，該機器可以使用5年，它可使每年勞動力成本減少1 200美元。舊機器在幾個月後需要進行一次大修理，預計修理費用為300美元。若購買了新設備，則新設備按直線法在5年內計提折舊，殘值為500美元。假定公司願意在投資收益超過資本成本（12%）的項目上投資。稅率為40%，公司應投資新設備嗎？

解答

求解投資成本。

計算由於投資使用新機器產生的現金流入增量。

求淨現值是否為正。

因為該投資的回報率稍高於資本成本，所以公司應購買新設備。

注意：我們從本例中可以看出折舊的重要性。由運營而引起的年金現值為：

（節約成本-稅金）×現值係數

（1 200-480）×3.605=2 596（美元）

該數字比投資成本3 700美元少1 104美元，只有當折舊抵稅作用特別大時，才值得投資。折舊抵稅的現值為1 009美元，計算方法如下：

（稅率×折舊差額）×現值係數

（0.4×700）×3.605=1 009（美元）

例C-3　自制還是外購的決策

Triple X公司製造和銷售冰箱。部分零件自制，部分零件外購。工藝設計部門認為當前外購價格為每件8.25美元的零件。如果自制的話可以削減成本。公司每年使用100 000件這種零件。會計部門在工藝設計部門估計的基礎上列出以下成本清單：

·固定成本將增加50 000美元；

·勞動力成本將增加125 000美元；

·企業經常費用將比現在的每年500 000美元增長12%；

·該零件的原材料成本為600 000美元。

根據以上估計，公司應該自制還是外購這種零件？

解答

自制零件的總成本如下。

自制零件的單位成本是：

公司應該繼續外購這種零件，因為自制零件的單位成本比外購高0.10美元。

本章小結

C-1用不同的成本、風險、期望值和折舊來評估資本投資

總結

·由於管理決策與資本投資有關，因此財務分析對運營與供應鏈管理是很必要的。我們在本附錄中討論了在運營與供應鏈管理中很有用的基本概念。

·我們分析了成本如何分類以及資產折舊的常用方法。我們也使用基於活動的成本分析將成本分為普通成本和間接成本。

·選擇投資時需要用中長期的眼光來看待投資。在進行投資時，需要分析資金的時間價值。可以藉助電子表格來做出相關決策。