附錄A　用Excel Solver解決線性規劃問題

充分利用可獲取的人力、物料、工廠和設備以及資金等資源是運營盈利的關鍵。現在管理者可以採用強大的數學模型工具——線性規劃來解決這些問題。在本附錄中，我們將介紹利用Microsoft Excel Solver來解決線性規劃問題是如何為具有創新意識的管理者打開一個嶄新世界的，併為那些想要進入諮詢行業的人介紹一種極其有用的、用來豐富其管理的工具，量化管理模型。在本附錄中，我們將用一個產品計劃問題來介紹這個工具的使用，找出在不同成本和資源要求的限制下的最優產品組合。這個問題顯然和當今市場的激烈競爭息息相關。真正成功的企業都會提供從普通產品到高檔奢侈型的一系列產品組合。所有這些產品都在爭奪有限的生產能力和其他能力。保持適當的產品組合能有力地支持企業資產的收益和回報。

我們首先簡要介紹一下線性規劃和其適用的情況，接著我們會用線性規劃的方法解決一個簡單的產品組合的問題。本書的其他章節也介紹了一些線性規劃在其他方面的應用。

線性規劃 （linear programming，LP）指的是對有限資源進行最優化配置的一些數學方法。LP是數學最優化方法中最常用的一種，它被用來解決許多生產管理問題。以下是線性規劃的常見應用。

總體銷售與運營計劃 ：制訂成本最小化的生產計劃。問題是要在生產能力和勞動力的限制條件下制訂3～6個月的生產計劃滿足預期的需求。在此過程中要考慮的問題包括：常規勞動力工作時間和加班時間、僱用和解僱、合同轉包和庫存持有成本。

服務/製造生產率分析 ：通過與績效最優的單元來比較，說明使用同樣資源的其他單元的效率是如何變化的。這將通過數據包絡分析（data envelopment analysis）來解決。

產品計劃 ：在不同成本和資源要求的幾種產品中選擇最優的產品組合，比如決定汽油、顏料、食品動物飼料等的化學成分。本附錄將說明有關該問題的例子。

產品生產路徑 ：一個產品依次經過幾個工作中心的加工，每個工作中心的機器的成本和產出特徵不同，根據已有的條件決定產品加工的最佳路徑。

交通工具/人員計劃 ：尋找利用飛機、公共汽車、卡車或者運營人員向客戶提供服務或者運輸不同地點之間的物料。

過程控制 ：盡力減少從整卷或者整張織物上切割鋼鐵、皮革或者織物產生的廢料。

庫存控制 ：在不同倉庫網絡或者庫存地點找到最優的產品放置組合。

分銷計劃 ：找到從工廠向倉庫配送產品或者在倉庫和零售商之間分銷產品的最優運輸方案。

工廠選址研究 ：通過評估不同地址方案之間以及不同供需資源之間的運輸成本，找到新工廠的最優選址。

物料處理 ：尋找使工廠中不同部門的物料處理成本最低的路徑。例如用卡車從供應倉庫運送物料到工作地點，每輛卡車的運送能力和表現是不同的。

由於運營細節信息的可獲取性增強，通過流程優化縮減成本也逐漸受到人們關注，線性規劃在眾多的行業都得到了廣泛採納。很多軟件供應商用企業資源計劃系統提供最優方案。一些企業將這些稱為高級計劃方案、同步計劃和流程優化。

一個問題具備了5種必要條件就適合線性規劃的方法。第一，必須有有限的資源（比如有限的工人、設備、資金、物料），否則就沒有問題。第二，必須要有明確的目標（比如利潤最大化或者成本最小化）。第三，必須存在線性關係（2是1的兩倍，如果製作一個部件需要3個小時，那麼製作兩個部件需要6個小時，製作3個部件需要9個小時）。第四，必須有同質性（同一臺機器上生產的產品都是相同的，或者每個工人的勞動工時的產出率都是相同的）。第五，必須有可分割性：一般線性規劃假設產品和資源可以分割為分數。如果這種分割並不可能實現（比如半架飛機、僱用半個工人），那麼可以採用線性規劃中的整數規劃。

當我們要實現單目標的最大化（利潤）或者最小化（成本）時，可以採用線性規劃；當我們要實現多目標的時候，可以採用目標規劃。如果一個問題在階段或者時間框架中最好解決，那麼我們要採用動態規劃。問題本身的其他一些限制要求可以用其他技術對問題進行求解，比如非線性規劃或者二次規劃。

A.1　線性規劃模型

一般說來，線性規劃問題就是一個最優化的過程，即選用非負的決策變量X1，X2，…，Xn 使目標函數最大化（或最小化）。公式為：

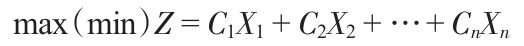
約束條件為：

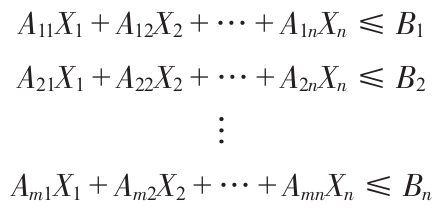
其中Cn 、Amn 和Bn 為常數。

根據實際問題，這些約束條件也可採用等號（=）或者大於等於號（≥）。

例A-1　Puck & Pawn公司

我們通過Puck & Pawn公司的一個例子來說明簡單線性規劃模型的解決步驟。Puck & Pawn生產曲棍球球杆和國際象棋。每個曲棍球球杆利潤為2美元，每副國際象棋利潤為4美元。每個球杆需要在A車間生產4小時，B車間生產2小時；每套象棋需要在A車間生產6小時，B車間生產6小時，C車間生產1小時。A車間每天可用的生產能力是120小時，B車間每天可用的生產能力是72小時，C車間每天可用的生產能力是10小時。

如果公司希望收益最大化，那麼每天應生產多少球杆和國際象棋？

解答

用數學公式表述這個問題。設H為曲棍球杆的數量，C為國際象棋的數量，利潤最大化的目標函數可以表述為：

max Z=2H+4C

這個最大化要受如下條件約束：

4H+6C≤120（A車間的限制）

2H+6C≤72（B車間的限制）

1C≤10（C車間的限制）

H，C≤0

這個公式滿足了本附錄開篇描述的標準線性規劃必需的5個條件：

（1）資源有限（每個機器加工中心可用的工作時間有限）。

（2）目標函數明確（我們知道變量代表什麼，也知道解決問題要達到的目標是什麼）。

（3）等式是線性的（沒有指數關係或者交叉產品）。

（4）資源是同質的（衡量方法是一樣的，都是機器工時數）。

（5）決策變量是可分的並且是非負的（我們可以生產一個分數的球杆或者象棋，當然，如果認為這樣是不合理的，我們可以使用整數規劃）。

A.2　圖解線性規劃

圖A-1　曲棍球杆和象棋問題的圖解

儘管圖解線性規劃 （graphical linear programming）的應用侷限在兩個決策變量的問題（3個決策變量採用三維圖形），但它可以快速揭示線性規劃的本質。我們利用Puck & Pawn公司用到的圖形方法來闡述圖形線性規劃的步驟。

（1）把問題構建成為數學模型。 例A-1已經給出了問題的等式。

（2）描繪約束條件等式。 約束條件很容易劃分，只要設一個變量為0，得到另一個變量在軸上的截距即可（這一步中約束條件的不等號可忽略不計）。對於機器中心A的約束條件而言，當H=0時，C=20；當C=0時，H=30。對於機器中心B的約束而言，當H=0時，C=12；當C=0時，H=36。對於機器中心C的約束條件而言，無論H為何值，C=10。圖A-1繪出了這些圖形。

（3）確定可行域。 每個約束條件的不等號的方向決定了可行方案所在區域。在本例中，所有的不等式都是小於等於的，這就意味著生產出來的產品數量組合不可能落到圖中任何一條約束線的右邊。圖A-1中可行解的區域是不規則的，並形成了一個凸多邊形。如果一個多邊形內任意兩點之間的連線保持在多邊形內部，那麼該多邊形為凸多邊形。如果可行域不是凸多邊形，那麼說明構建問題方程的時候出現了錯誤或者該問題不適用於線性規劃。

（4）描繪目標函數。 目標函數可以這樣描繪，先假設一個任意的總利潤額，然後求出軸上的截距座標，就像在描繪約束條件等式時那樣操作。本附錄中用到的目標函數的其他形式是等利潤或者等貢獻線，因為它能列出任何給定利潤額的所有可能的產品組合。例如，從圖A-1中離原點最近的虛線上我們可以得到利潤為32美元的曲棍球杆和象棋的所有生產組合，只要選定線上一點，就可以知道該點每種產品的數量。在a點32美元的收益組合是10根曲棍球杆和3副象棋。只要把H=3、C=10代入目標函數就可以驗證：

2×10+4×3=20+12=32（美元）

（5）尋找最優點。 通過數學方法可以發現決策變量的最優組合一般在凸多邊形的頂點（交點）上得到。圖A-1中有4個頂點（不包括原點），用以下兩種方法中的任意一種都可以找出哪個是最優點。第一種方法是用代數的方法求出不同頂點的目標函數值。這要求解一對等式約束並把結果代入目標函數。例如，用以下方法求解2H+6C=72和C=10的交點：把C=10代入2H+6C=72，即2H+6×10=72，2H=12，即H=6。

再把H=6和C=10代入目標函數，得到：

利潤=2H+4C=2×6+4×10=12+40=52（美元）

這種方法還可以直接從圖A-1中讀出H和C的值，並把結果代入目標函數，計算方法和前面一樣。這種方法的缺點是當問題的約束條件很多時，就需要估算很多的可能點，而且數學計算每個可能組合的效率非常低。

第二種是採用用目標函數或者等利潤線來尋找最優點。該過程就是畫一條平行於任意初始等利潤線的直線，並且令該利潤線離原點最遠（在成本最小化問題中，目標是畫一條線令其通過最接近原點的那個點）。在圖A-1中，標著2H+4C=64美元的虛線貫穿最靠外的交點。注意這個任意的等利潤線要能反映特定問題目標函數的斜率。不同的目標函數（如利潤=3H+3C）會得出不同的距離原點最遠的點。假設2H+4C=64美元是最優的，那麼需要生產的每個變量值從圖A-1中可以讀出：24根球杆和4副象棋，再也沒有別的產品組合能獲利更多。

A.3　用Excel進行線性規劃

電子數據表可以用來解決線性規劃問題。Microsoft Excel有一個最優化工具叫Solver（規劃求解），我們用曲棍球杆和象棋的問題來說明它的用法。我們從工具菜單選擇規劃求解，這時彈出對話框要求提供規劃求解參數。接下來我們將描述如何用Excel來解決我們的例子。

如果你的工具菜單中沒有規劃求解的話，單擊加載宏，選擇加載“規劃求解”，單擊“確定”。這樣以後用到規劃求解都可以直接由工具菜單上直接選取。

在下面的例子裡，我們將逐步建立電子數據表解決Puck & Pawn公司的問題。我們的基本策略是首先用電子數據表定義問題。因此，我們首先單擊規劃求解，輸入所需的信息。然後，我們執行規劃求解並且解釋規劃得出的報告的結果。

第1步：定義可變單元格。 首先確定一個問題的決策變量要採用的單元格，在例A-1中是曲棍球杆數H和需要生產的象棋套數。Excel在規劃求解中把這些單元稱為可變單元格。在圖A-2的Excel截圖中，我們用B4單元格表示曲棍球杆數量，用C4單元格表示國際象棋套數。注意我們把一些單元格的初始值設定為2，當然我們可以給這些單元格賦予任何值，但最好用非零值，因為這樣容易驗證我們的計算是否正確。

第2步：計算總利潤（或者總成本）。 總利潤或者總成本就是我們的目標函數，通過把各個產品的單位利潤和產品數量相乘、加總，最後得到總利潤值。我們把單位利潤放在單元格B5和單元格C5中（$2和$4），因而可以用以下等式來計算利潤：B4*B5+C4*C5，將計算結果放在D5中。規劃求解把這一單元格稱為目標單元格，它反映了一個問題的目標函數值。

第3步：建立資源利用情況。 我們的資源是例A-1中的車間A、B和C。我們在電子數據表裡面設立3行（9、10和11），每一行建立一個資源約束。對於車間A，每生產一根曲棍球杆的加工時間為4小時（單元格B9），每生產一副國際象棋的加工時間為6小時（單元格C9）。對於一個特定方案，D9得出車間A所用的資源（B9*B4+C9*C4）。E9的小於等於號說明我們希望車間A採用的生產能力小於等於120小時（F9中的數據）。第10行和第11行用同樣的方法建立車間B和車間C的資源約束。

圖A-2　Puck & Pawn公司的Excel截屏圖

第4步：設置求解過程。 進入工具菜單選擇規劃求解。

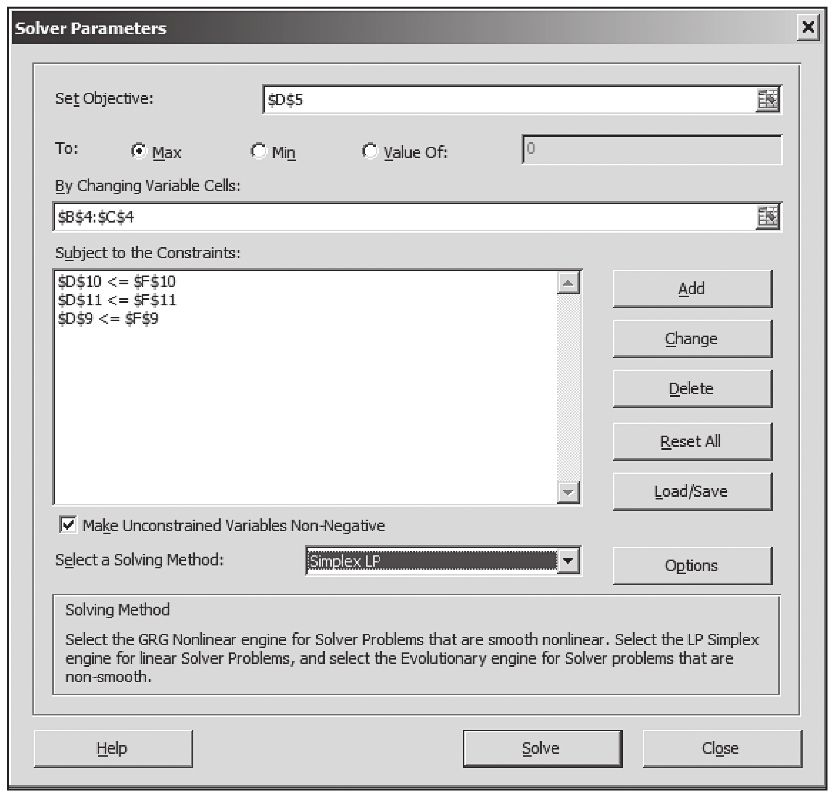
（1）設置目標單元格：我們想要計算的優化結果放置的位置。在例A-1中是電子數據表中D5計算的利潤值。

（2）等於：由於我們要求最大利潤，所以該項設置為最大。

（3）可變單元格：規劃求解過程中為求得最大利潤值可以變化的單元格。在例A-1中B4～C4是變化單元格。

（4）約束：根據車間的生產能力設置。這時我們單擊“添加”列出利用的資源總數要小於等於可利用的生產能力。例如車間A的約束如下左圖所示，每個約束方程確定以後單擊“確定”。

（5）選項：單擊“選項”，我們可以規定規劃求解解決問題的類型和方法。規劃求解有很多選項，但我們要用到的僅有很少一部分。

多數選項都是關於規劃求解如何解決非線性問題。非線性問題一般較難解決，並且很難找到最優值。幸運的是，我們的問題是一個線性的問題，因為我們的約束條件和目標函數都是用線性等式來計算的，所以我們很容易知道這一點。單擊“採用線性模式”說明我們想要採用線性模式來解決問題。此外我們已知可變單元格（決策變量）一定是非負數，因為如果曲棍球杆或者國際象棋的產量小於0就沒有任何意義了。我們選擇假定非負作為選項。我們現在就可以用規劃求解來解題了，單擊“確定”回到規劃求解參數對話框。

第5步：解決問題。 單擊“規劃求解”。我們立即得到如下右圖所示的規劃求解結果。

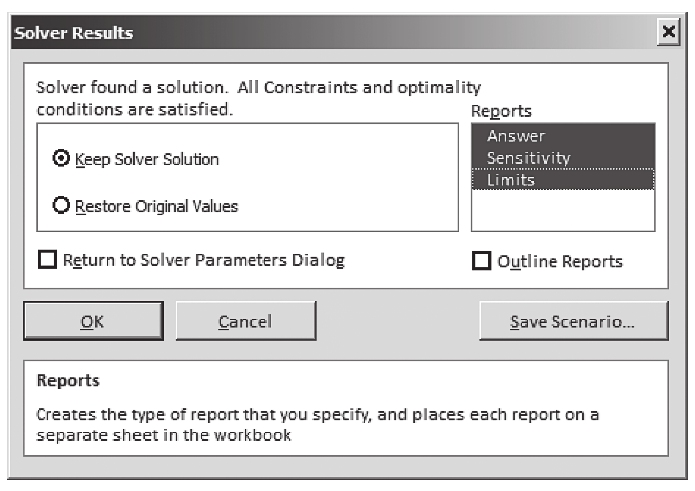
規劃求解報告說明找到了一個看似最優的方案。對話框右面有三個選項：運算結果報告、敏感度報告、極限值報告。單擊所有的選項令規劃求解給出這些報告。當這些報告都被選中的時候，單擊“確定”返回到數據表，Excel根據要求生成了3個表格。

對問題最有用的報告是運算結果報告和敏感性報告，如表A-1所示。運算結果報告顯示了總利潤的最終結果（64美元）和生產的數量（24根球杆和4副象棋）。在運算結果報告中的約束條件部分，給出了每種資源的狀態。機器中心A和B都被充分利用，而機器中心C還有6單位的空閒能力。

表A-1　Excel規劃求解報告和敏感性報告

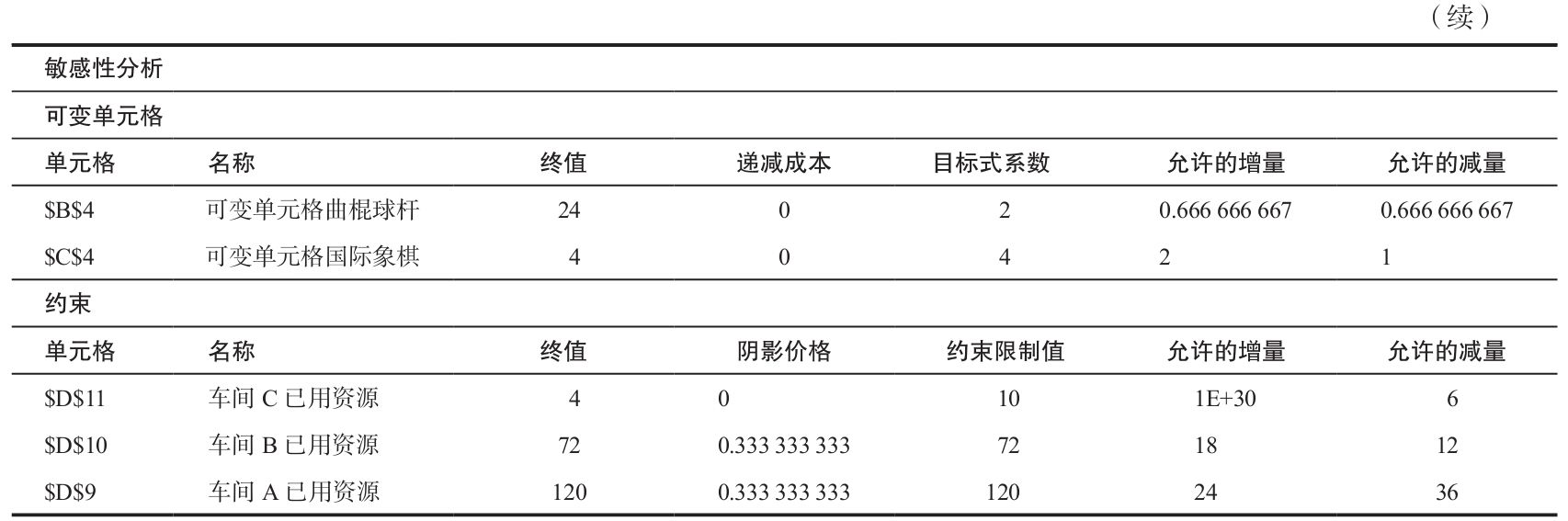
敏感性報告分為兩部分。第一部分標題為“可變單元格”，對應於目標函數係數。每根球杆的利潤上浮或者下浮0.67美元（在2.67美元和1.33美元之間）對結果沒有影響。同理，象棋的價格在6美元和3美元之間，對結果沒有影響。Ａ車間的能力可以上漲到144（=120+24）或者下調到84，這樣對目標函數造成每單位0.33美元的漲幅或跌幅。B車間可以上漲到90或者下調到60，同樣對目標函數造成每單位0.33美元的漲幅或跌幅。對於C車間，可以上漲到無窮大（1E＋30是一個極大數的科學計數）或者下調到4，都不會對目標函數產生影響。

本章小結

A-1　利用Excel Solver解決線性規劃問題

總結

·線性規劃是業務分析很重要的工具，它允許管理者最有效地利用現有資源如原材料、工廠等。

·利用Excel Solver，我們可以解決線性規劃的問題，融合了銷售、計劃、服務和製造分析、產品計劃、產品路線以及其他更多的因素。

·在Excel Solver中，線性規劃問題遵循以下步驟：定義變化單元格、計算總利潤（或者總成本）、建立資源利用情況、設置求解過程、解決問題。

關鍵術語

線性規劃（LP）：指以最優方式在競爭需求之間分配有限資源的幾種相關數學技術。

圖解線性規劃：以直觀的形式快速掌握線性規劃的本質。

應用舉例

例1

一家傢俱工廠生產三種產品：茶几、沙發和椅子。這些產品要在5個部門中進行加工：鋸木、裁布、打磨、染色以及組裝部門。茶几和椅子只要用到原木、沙發需要木材和織物。膠水和縫合線十分充裕，它們所佔成本比較低，包含在運營費用中。每種產品的特定要求如下。

公司的直接勞動力成本是每月75 000美元，總共1 540工時，每小時48.7美元。根據現有的需求，公司每月可以售出300個茶几、180個沙發和400把椅子。茶几的銷售價格是400美元、沙發是750美元、椅子是240美元。假設勞動力成本是固定的，公司下個月不打算僱用或者解僱任何員工。

1.傢俱公司最有限的資源是什麼？

2.要使利潤最大化，公司的產品組合是怎樣的？每月應生產多少茶几、沙發和椅子？

解答

設每月生產茶几的數量為X1 ，沙發的數量為X2 ，椅子的數量為X3 。利潤是每件產品的收入減去物料成本（木材和織物），再減去勞動力成本。由於勞動力成本是固定的，我們將它們扣除，在數學上，我們有：（400-100）X1 +（750-75-175）X2 +（240-40）X3 -75 000。利潤的計算如下：

利潤=300X1 +500X2 +200X3 -75 000

約束條件如下：

木材：10X1 +7.5X2 +4X3 ≤4 350

織物：10X2 ≤2 500

鋸木：0.5X1 +0.4X2 +0.5X3 ≤280

裁布：0.4X2 ≤140

打磨：0.5X1 +0.1X2 +0.5X3 ≤280

染色：0.4X1 +0.2X2 +0.4X3 ≤140

組裝：1X1 +1.5X2 +0.5X3 ≤700

要求：

茶几：X1 ≤300

沙發：X2 ≤180

椅子：X3 ≤400

第1步：確定可變單元格。 在本題中為B3、C3和D3，注意到這些單元格的值設為0（見下圖）。

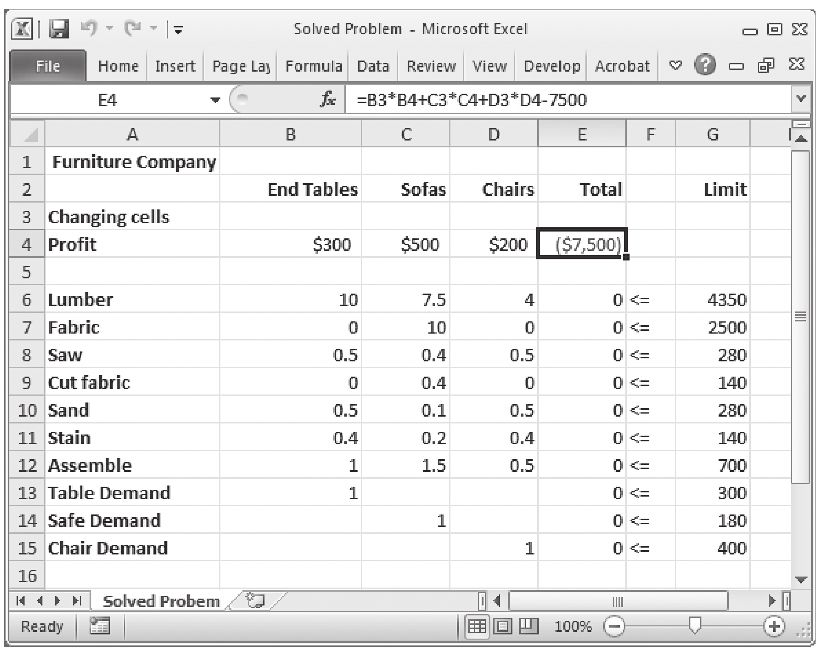
第2步：計算總利潤。 在本題中是E4（=300*B3+500*C3+200*D3-75 000）。注意到75 000美元的固定成本已經從收入中減掉了。

第3步：確定資源利用情況。 單元格E6～E15是每種資源的利用情況，是由B3、C3和D3分別乘以各種產品的資源消耗量，再加總得到的（如E6=B3*B6+C3*C6+D3*D6）。各種資源的約束輸入在單元格F6～F15中。

第4步：設定規劃求解選項。 單擊“工具”，選擇規劃求解選項（見下圖）。

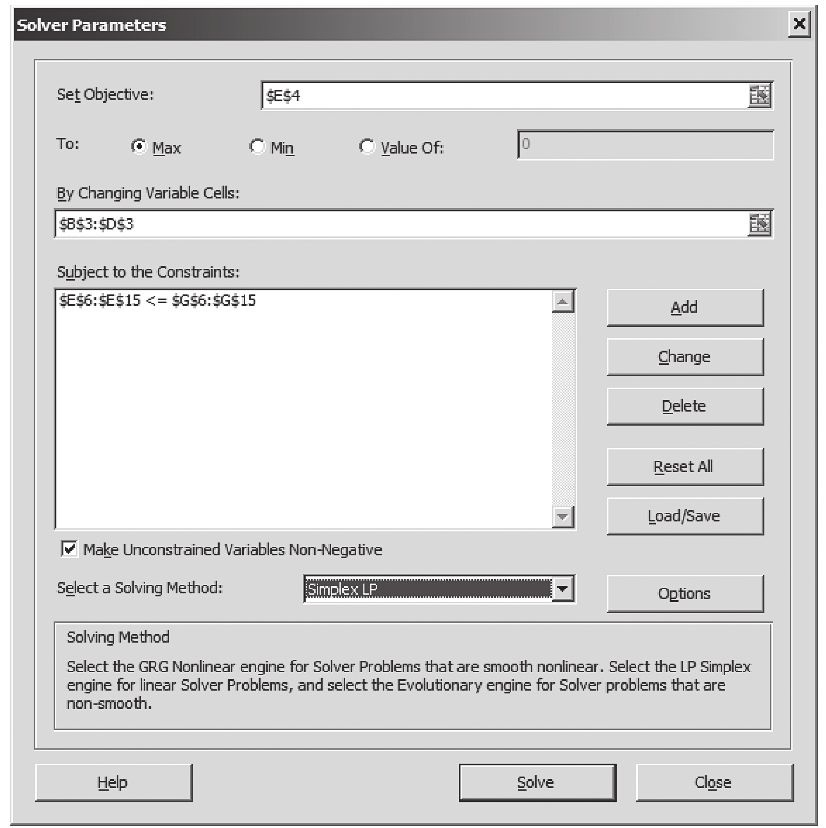
a.設定“目標單元格”：我們希望計算出最優值的單元格。

b.等於：由於要求利潤最大化，選擇“最大值”。

c.可變單元格：規劃求解為使利潤最大化可以改變取值的單元格（在本題中為單元格B3～D3）。

d.約束：添加約束條件的地方，我們設定E6～E15的值小於等於G6～G15（見下圖）。

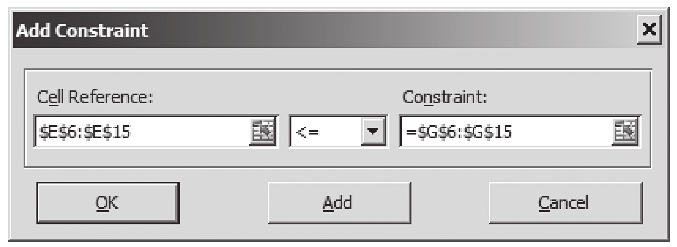
第5步：選擇一種解法。 這裡有很多選項，但是為達到求解目的，只需要選擇“採用線性模型”和“假定非負”。“採用線性模型”意味著我們所有的方程都是簡單的線性等式。“假定非負”表明可變單元格的值必須大於等於0。

第6步 ：單擊“求解”獲得結果。 我們可以看到“規劃求解結果”中顯示找到了一個解，兩種報告形式被選中。注意在圖中顯示的對話框中，規劃求解顯示找到了一個解並且滿足所有約束條件達到最優。在右邊的報告選項框中，運算結果、靈敏度和極限值報告都被選中了，表明我們想要了解這些結果。選中這些報告之後，單擊“確定”返回到原來的數據表。

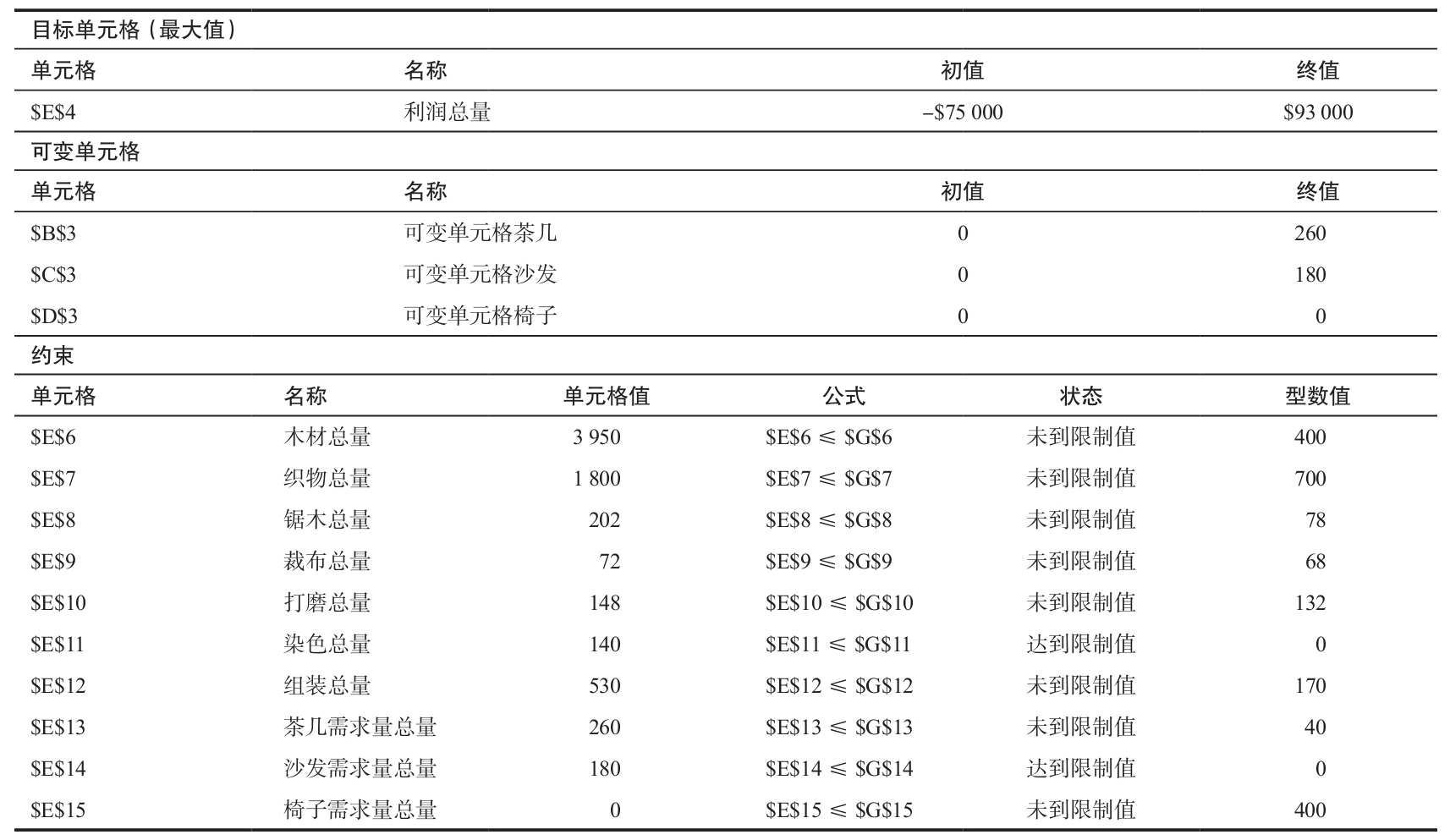
我們看到生成了三張新表：運算結果報告、敏感性報告、極限值報告。運算結果報告顯示利潤是93 000美元（一開始是-75 000美元），應該生產260個茶几，180個沙發，不生產椅子，在說明有關約束的表格中我們看到只有染色時間和沙發的需求達到了限制值。我們能從“狀態”欄看到是否到達了極限值。未到限制值表示還有鬆弛，由最後一欄數值可以看到。

當然，我們可能對這個結果並不滿意，因為我們沒有滿足所有茶几的需求，並且完全不生產椅子似乎是不明智的。

敏感性報告（見後面的表格）對結果做了進一步解釋。報告的可變單元格部分顯示了每個單元格的終值和遞減成本。遞減成本說明當前設置為0的單元格發生變化時目標單元格會發生的變化。由於當前茶几（B3）和沙發（C3）不為0，它們的遞減成本為0。而我們每增產一把椅子（D3），目標單元格值會減少100美元（為了方便解釋對這些數據進行舍入）。可變單元格的最後3列是數據源數據表中的目標式係數以及允許的增量和允許的減量。允許的增減表示利潤係數可以在哪個範圍內變動而不影響可變單元格的值（當然目標單元格的值會變）。舉例來說，每個茶几的收入可能高達1 000美元（=300+700）或是低到200美元（=300-100），我們仍然每個月賣260個茶几。記住這裡假定除了某產品的利潤係數以外，其他量不變。注意沙發的允許增量是1E+30。這是一個很大的數據，本質上是科學計數法表示的無窮大。

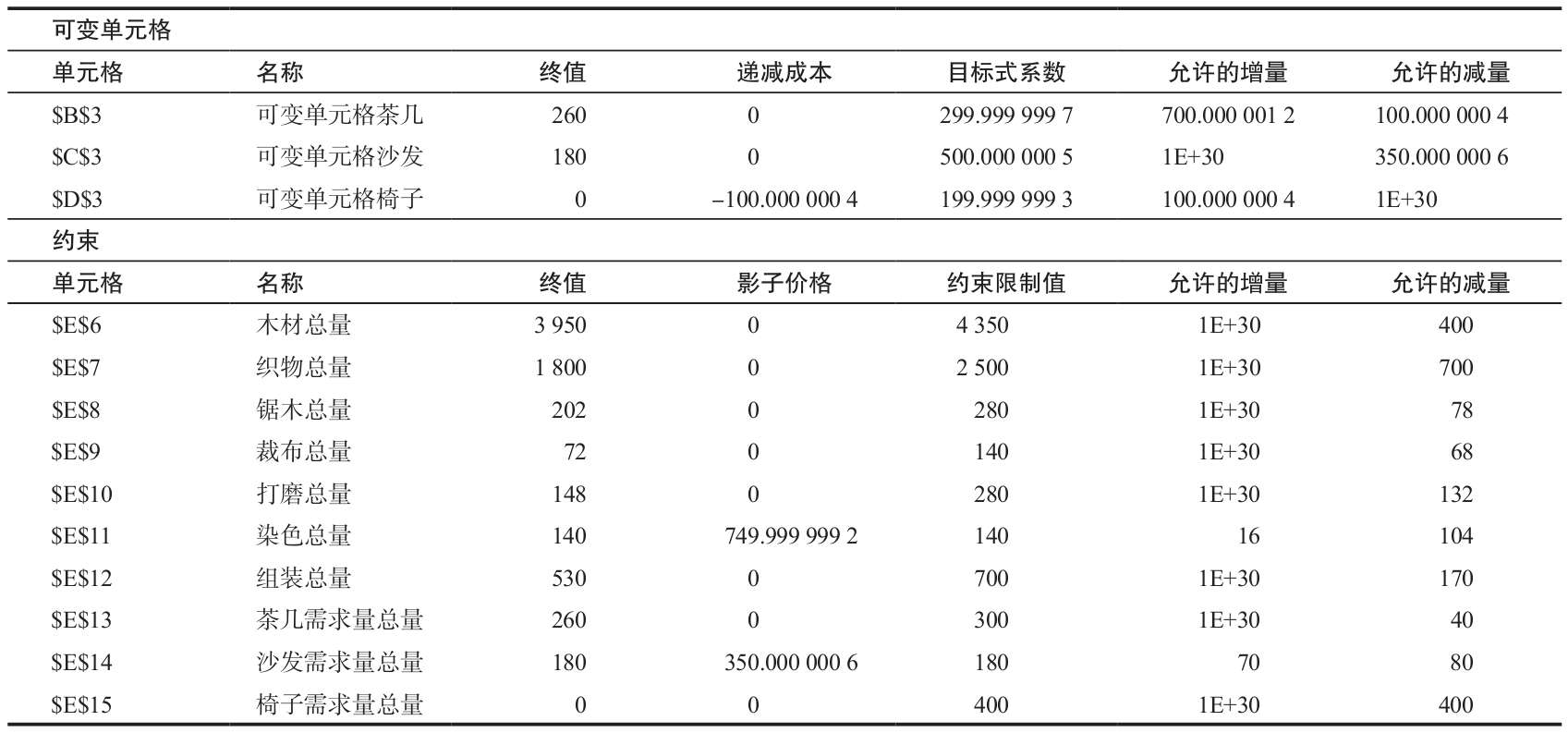
對於報告的約束部分，每種資源的實際利用情況在“終值”欄表示出來。“影子價格”是指某種資源一單位的增量對目標單元格價值的貢獻。如果我們能增加染色的生產能力，每增加一小時帶來的利潤增加額是750美元。“約束限制值”是當前每種資源的限制。“允許的增量”是影子價格保持不變時資源允許增加的量。用於染色的工作時間再增加16小時，每小時的影子價格還是750美元。類似地，“允許的減量”表示保持影子價格不變時，各種資源總額允許的減少量。在這張表上還有一些有價值的信息。

極限值報告為我們的問題提供了一些其他信息（見下表）。

目前方案的總利潤是93 000美元。B3（茶几）目前的值是260單位。如果這個值減少到0，利潤就會減少到15 000美元。B3為上限極限260單位時，利潤是93 000美元（當前值）。類似地，對C3（沙發），C3為上限極限180單位時，利潤是93 000美元，如果減少到0，利潤會減少到3 000美元。對D3（椅子），若減為0，利潤是93 000美元（當前值），在本例中，上限極限也是0。

問題的可行答案如下。

1.傢俱公司最有限的資源是什麼？

答案：對我們的生產資源來說，最關係到利潤的是著色的時間。我們可以再增加16小時的能力。

2.要使利潤最大化，公司的產品組合應該是怎樣的？每月應生產多少茶几、沙發和椅子？

答案：產品組合應該是260個茶几、180個沙發、不生產椅子。

當然，我們僅僅簡單地考慮了這個問題。實際上我們可以嘗試增加染色的生產能力，這樣會產生新的緊缺資源。我們也可以設置每種產品必須至少生產某個量的情景，這也可能更貼近現實一點。這能幫助我們決定如何重新配置勞動力資源。

例2

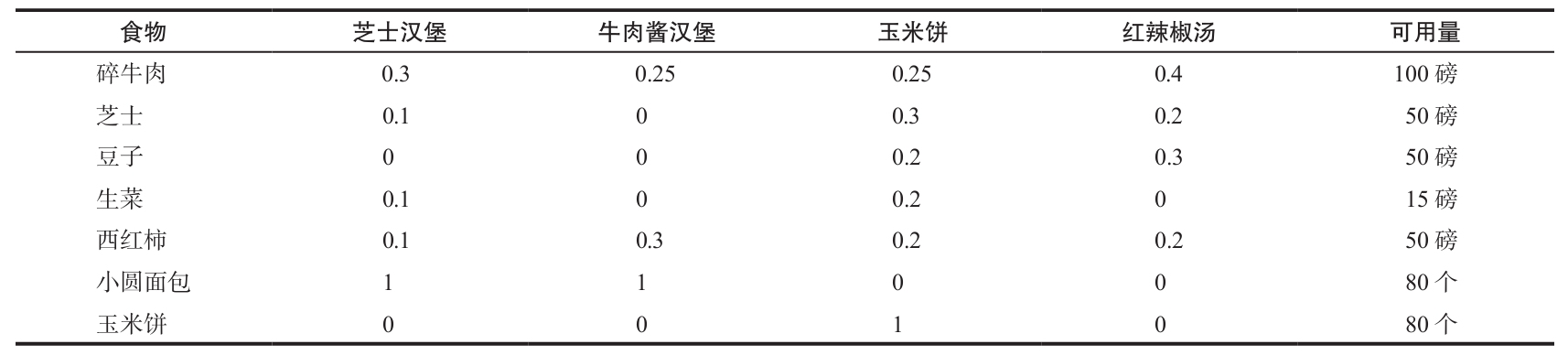
週五下午2點，Bruce’s Diner的高級廚師（烤肉廚師）Joe，正在決定如何為當天晚上的4道特餐分配有限的原材料。當天下午一開始就要做好決定，因為有3道菜現在就要開始準備了（牛肉醬漢堡、玉米餅和紅辣椒湯）。下表包含了庫存的食物和每道菜需要的原材料用量。

Joe另外要考慮的一個因素是市場需求預測和售價。

Joe購買了所需的所有原材料，放置在冷卻器中，他希望獲得最大利潤。

要求：

1.為使收入最大化，Joe為週五特餐準備的最佳組合是什麼？

2.如果某個供應商以1.00美元一個的應急價格提供小圓麵包，值得花錢購買嗎？

解答

設X1 為週五特餐準備的芝士漢堡的數量，X2 為牛肉醬漢堡的數量，X3 為玉米餅的數量，X4 為紅辣椒湯的數量。

收入=2.25X1 +2.00X2 +1.75X3 +2.50X4

約束條件如下。

碎牛肉：　　0.30X1 +0.25X2 +0.25X3 +0.40X4 ≤100

芝士：　　　0.10X1 +0.30X3 +0.20X4 ≤50

豆子：　　　0.20X3 +0.30X4 ≤50

生菜：　　　0.10X1 +0.20X3 ≤15

西紅柿：　　0.10X1 +0.30X2 +0.20X3 +0.20X4 ≤50

小圓麵包：　X1 +X2 ≤80

玉米餅：　　X3 ≤80

需求：

芝士漢堡：　X1 ≤75

牛肉醬漢堡：X2 ≤600

玉米餅：　　X3 ≤100

紅辣椒湯：　X4 ≤55

第1步： 指定可變單元格，在該題中是B3、C3、D3和E3。初值取為10以便檢查公式是否有誤（見下圖）。

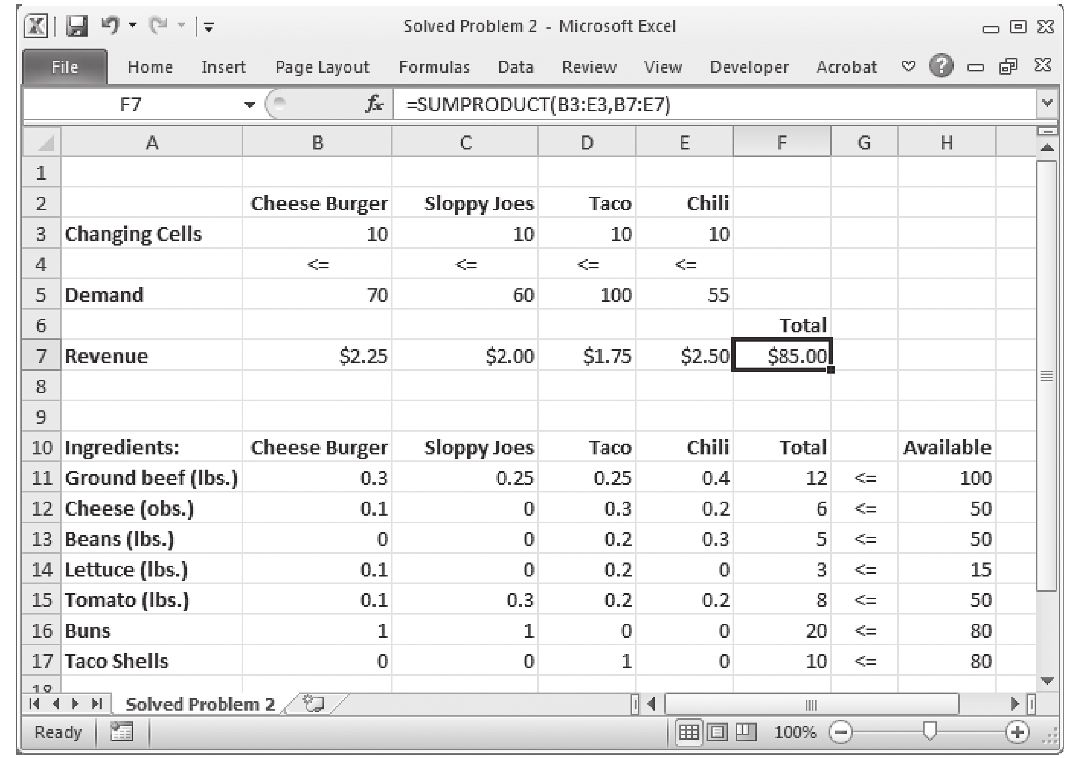
第2步： 確定總收入的公式——F7（B3乘以芝士漢堡2.25美元的單位利潤，加上C3乘以牛肉醬漢堡2.00美元的單位利潤，加上D3乘以玉米餅1.75美元的單位利潤，加上E3乘以每碗紅辣椒湯2.50美元的單位利潤，Excel裡面的SUMPRODUCT功能可以快速進行該項計算）。注意到當前值是85美元，因為可變單元格初始值是10。

第3步： 確定每種原材料的利用情況——單元格F11～F17，每種原材料的使用量通過可變單元格與對應係數的乘積之和得到。每種原材料的約束限制由H11～H17列出來。

第4步： 設置規劃求解，對選項進行設置（見下圖）。

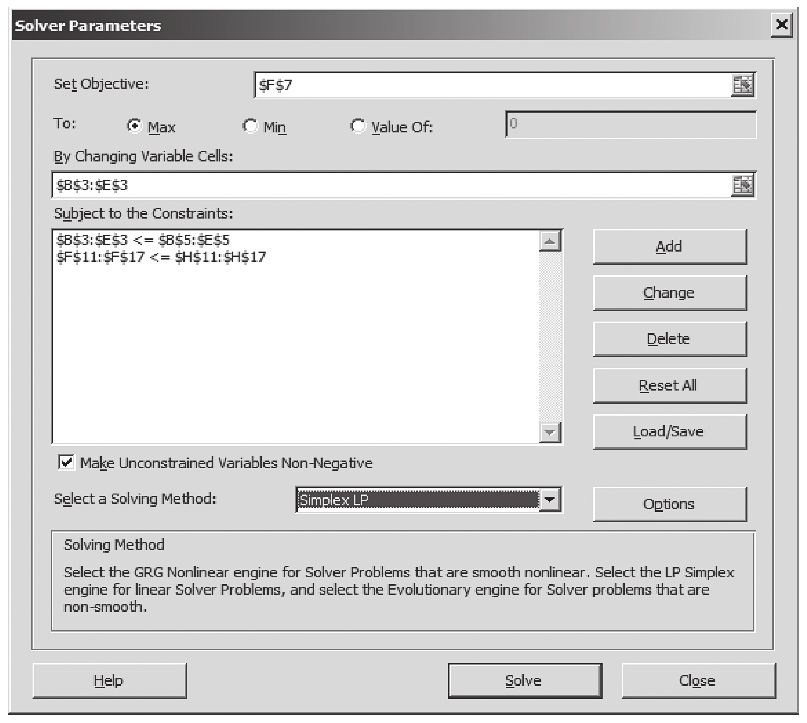
a.設置“目標單元格”。把我們要進行最優值計算的單元格設為目標單元格。在這張表中，收入的計算值設定在F7單元格。

b.等於：希望最大化結果時選擇“最大值”。

c.可變單元格：告訴我們每種食品該生產多少的單元格。

d.約束：我們在這裡添加兩類約束，一是需求約束，一是原材料使用約束。

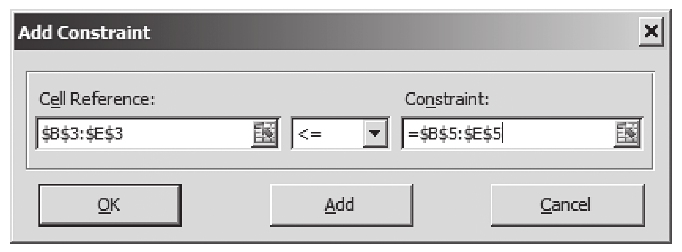
第5步： 設置“選項”。單擊“選項”，我們把所有選項設置為默認，除了兩個之外：①我們必須選定採用線性模型；②我們必須選定假設非負。這兩個選項規定規劃求解為線性規劃問題，並且所有的可變單元格都為非負。

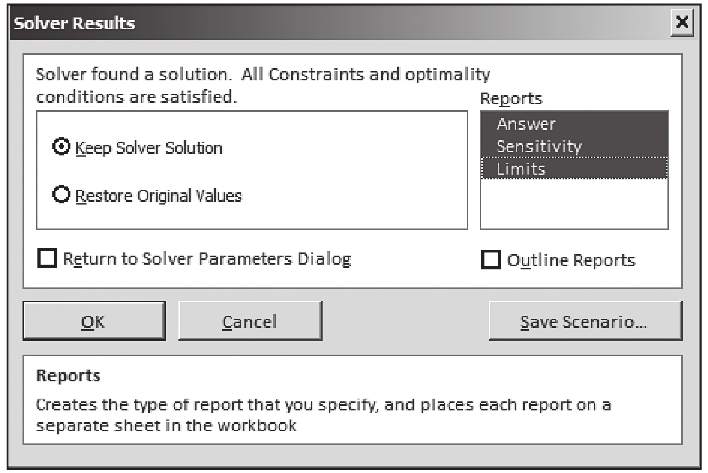
第6步： 單擊“求解”，出現“規劃求解結果”對話框。確認這個對話框上寫著“規劃求解找到一解，可滿足所有的約束及最優狀況”（Solver found a solution.All Constraints and optimality conditions are satisf ied，見下圖）。

在對話框的右邊可對三個報告選項進行選擇：運算結果報告、敏感性報告和極限值報告。單擊這三個報告，使它們變為亮色，再單擊“確定”，就可以返回到原工作表，但這時有了三個新表。

運算結果報告顯示目標單元格的終值是416.50美元，初值是85美元。在可變單元格區我們看到應該做20個芝士漢堡、60個牛肉醬漢堡、65個玉米餅和55碗紅辣椒湯。這就回答了第一個問題，即週五特餐準備的食品組合應該是什麼。

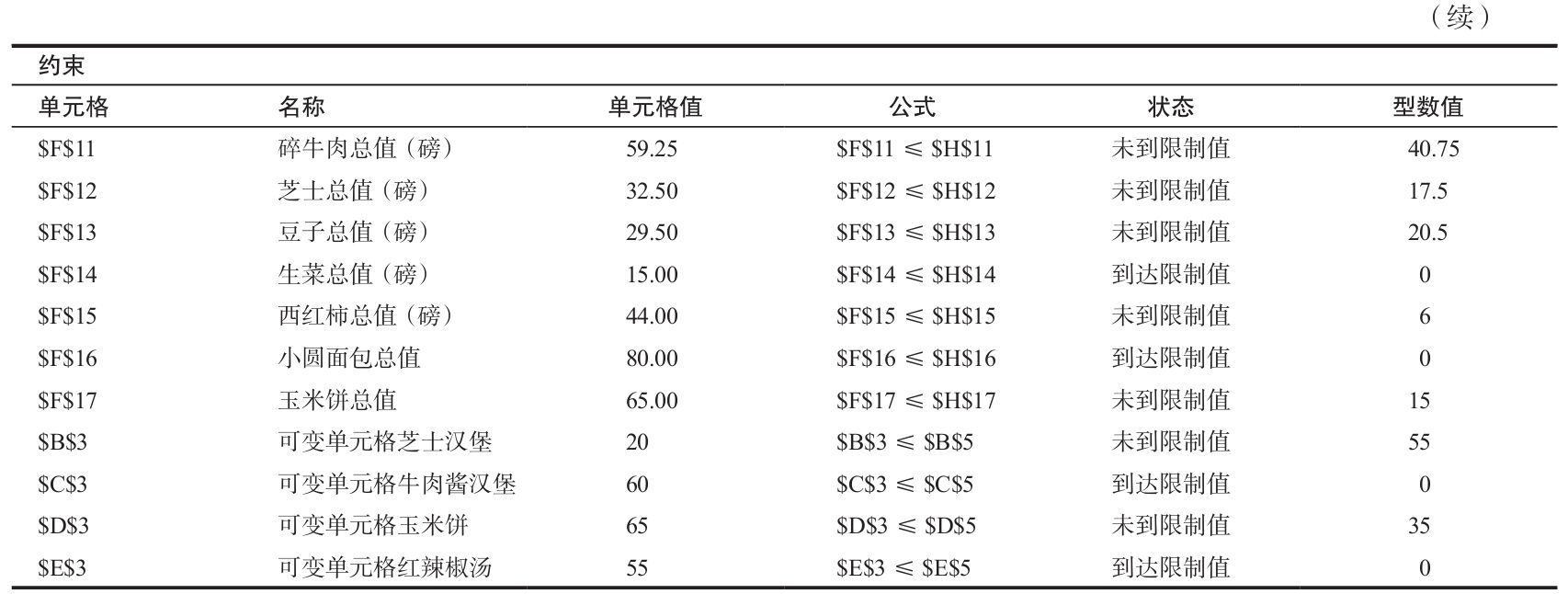
第二個問題為是否值得購買1.00美元價格的小圓麵包。運算結果報告顯示小圓麵包的使用已經達到了限制值，因此買更多的小圓麵包是能夠盈利的，但是運算結果報告並沒有告訴我們用1.00美元的價格買進是否合算。為了回答這個問題，我們要看敏感性報告（見下表）。

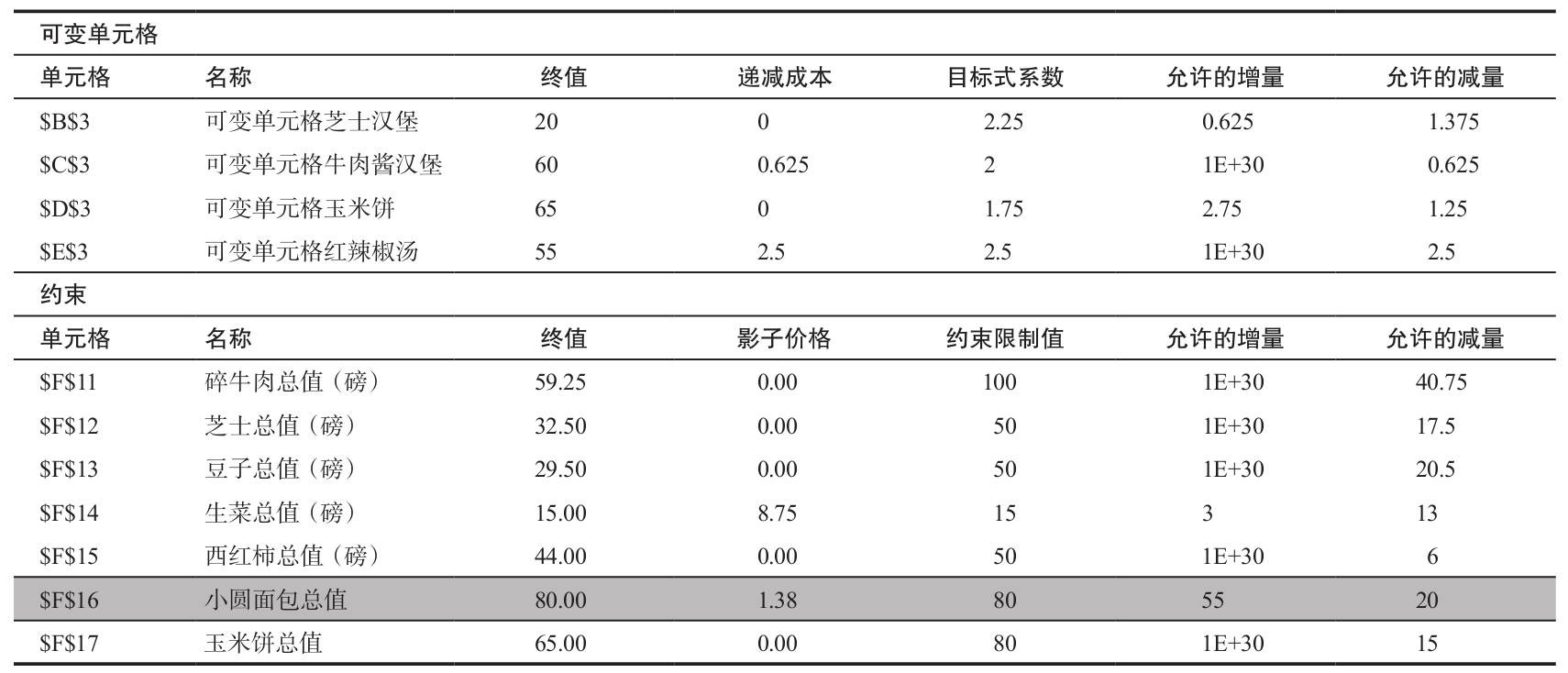
我們可以看到小圓麵包的影子價格是1.38美元，表示每增加一單位小圓麵包可以產生1.38美元的收入。我們同樣可以看到碎牛肉的影子價格是0，這是因為碎牛肉的使用量並沒有達到限制值，還有多餘。另外一個重要的信息是小圓麵包增加的數量不能超過55個，每個才價值1.38美元，這就是為什麼允許的增量是55。我們還看到每磅生菜值8.75美元。尋找生菜的應急供應商是明智的，因為它可以增加週五特餐的利潤。

問題的答案如下。

1.為使收入最大化，Joe為週五特餐準備的最佳組合是什麼？

答：20個芝士漢堡、60個牛肉醬漢堡、65個玉米餅和55份紅辣椒湯。

2.如果某個供應商以1.00美元一個的應急價格提供小圓麵包，值得花錢購買嗎？

答：值得。每增加一單位的小圓麵包帶來1.38美元的收入，而只有1.00美元的成本，因此有0.38美元的淨利潤，但是這在購買數量不超過55個的情況下才成立。

客觀題

1.用Excel Solver規劃求解解決如下問題：

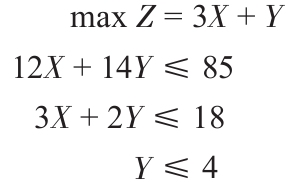
2.用Excel Solver規劃求解解決如下問題：

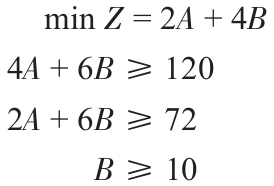
3.一家工廠停產了某種無利可圖的產品，導致產生了相當大的過剩生產能力。管理部門決定利用過剩生產能力生產X1、X2、X3三種產品中的一種或多種。

所需的機器時間如下表所示。

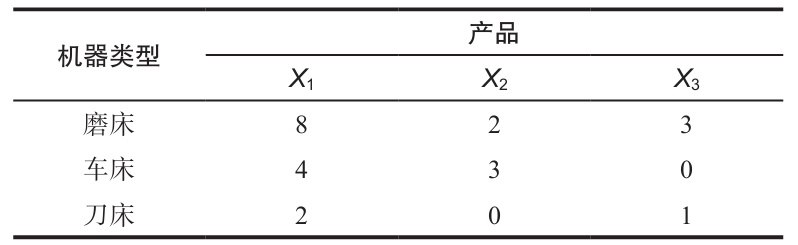
每週可用的機器時間如下表所示。

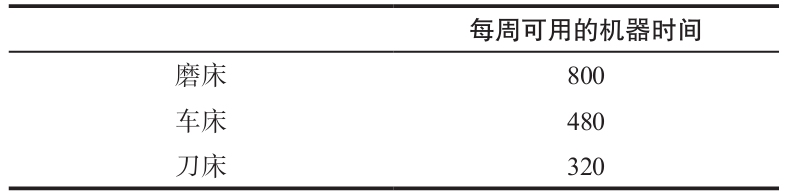
銷售人員預測可以售出所有的X1和X2，但X3每週最大的銷量為80件。

3種產品的單位利潤如下表所示。

a.構造可用來求解每週利潤最大化的規劃模型。

b.用Excel Solver規劃求解該問題。

c.最優解是什麼？每種產品各生產多少？相應的利潤是多少？

d.機器情況如何？它們都滿負荷工作還是仍有可用時間？X3是以最大銷量銷售嗎？

e.假定磨床每週還有200小時的工作時間可用。增加的成本1.50美元/小時。你建議這樣做嗎？說出你的理由。

4.亞利桑那州大學宿舍計劃準備一種食物，目標是使學生花費成本最低，但食物必須包含1 800～3 600卡路里的熱量。攝入澱粉不能超過1 400卡路里，攝入蛋白質不能低於400卡路里。各種食物只能有A和B兩種組成。A每磅0.75美元，包含600卡路里，其中400卡路里是蛋白質，200卡路里是澱粉。每個學生食用的A不能超過2磅。B每磅0.15美元，包含900卡路里，其中700卡路里是澱粉，100卡路里是蛋白質，100卡路里是脂肪（答案見附錄D）。

（1）寫出代表這些信息的等式。

（2）用圖形法求出所需各種食物的數量。

5.在第4題上加上不超過150卡路里脂肪的限制條件，並將A的價格提升到1.75美元/磅，B的價格提升到2.50美元/磅，再次求解。

6.洛根公司想混合兩種燃料（A和B）以使它的卡車成本最低。卡車每月至少需要3 000加侖燃料。卡車燃料容量最大為4 000加侖。現有2 000加侖A和4 000加侖B可用。混合燃料的辛烷含量要在80%以上。

當燃料混合時，得到的混合量和加入的量相等。辛烷的含量是單種燃料的加權平均，權數是各種燃料佔重量的比例。

已知：燃料A的辛烷含量是90，每加侖成本是1.2美元；燃料B的辛烷含量是75，每加侖成本是0.9美元。

（1）寫出能表達這些信息的等式。

（2）根據已知條件給出的每種燃料的用量，用Excel Solver規劃求解這個問題。列出解答問題必要的假設。

7.假設你要對你的可支配收入做一個預算。你一個月最多有1 500美元可用於食物、住宿及娛樂。花在食物和住宿上的費用不能超過1 000美元，單獨花在住宿上的費用不能超過700美元，娛樂不能超過300美元。花在食物上的每一美元的滿意度為2，花在住宿上的每一美元的滿意度為3，花在娛樂上的每一美元的滿意度為5。

假設預算問題是線性關係，用Excel Solver規劃求解來決定資金的最優分配。

8.C鎮釀酒廠釀造兩種啤酒：Expansion Draft和Burning River。Expansion Draft每桶售價為20美元，而Burning River每桶售價8美元。釀造一桶Expansion Draft需要8磅穀物和4磅蛇麻草，釀造一桶Burning River需要2磅穀物、6磅稻子和3磅蛇麻草。假定這些配比是線性的，用Excel Solver規劃求解Expansion Draft和Burning River的最優產量，使C鎮的收入達到最高。

9.BC Petrol在他們Kentucky的化工廠生產3種化學藥品：BCP1、BCP2、BCP3。這3種藥物可用兩種作業生產：自動作業和人工作業。自動作業每小時成本為48美元，可以產出3單位BCP1、1單位BCP2和1單位BCP3；人工作業每小時成本為24美元，可以產出1單位BCP1和1單位BCP2。為滿足顧客需求，每天至少要產出20單位BCP1、10單位BCP2和6單位BCP3。假定線性關係，用Excel Solver規劃求解使成本最優且能滿足顧客需求的自動作業和人工作業的組合。

10.Wood縣的一個農民擁有900英畝地。她準備在每英畝地上種植玉米、大豆或者小麥。一英畝地如果種玉米可獲得2 000美元利潤，種大豆可獲得2 500美元利潤，種小麥可獲得3 000美元利潤。她有100個勞動力和150噸肥料。

下表是每英畝地農作物的所需。假定該問題是線性關係的，用Excel Solver規劃求解可以使利潤最大的玉米、大豆和小麥的生產組合。